C++——STL容器【priority_queue】模拟实现

本章代码：优先级队列模拟实现、priority_queue文档

1. priority_queue介绍

priority_queue在STL里面是队列的一种，叫做优先级队列，它的底层是基于堆实现的，默认的是大堆。

它的使用方法与queue类似，可理解为priority_queue是一个可以排序的队列

2. priority_queue模拟实现

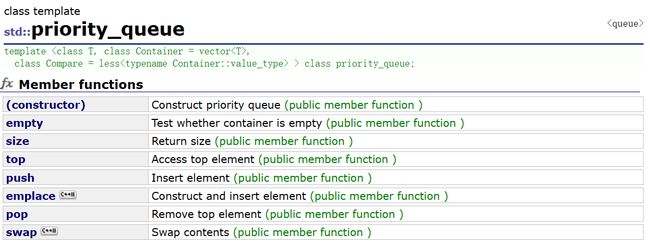
先查看文档，看看支持了哪些接口：

2.1 构造函数

priority_queue采用的vector作为容器适配器，那默认构造直接调用vector的就行，然后构造还支持迭代器初始化：

priority_queue()
{}

template<class InputIterator>
priority_queue(InputIterator first, InputIterator last)
{
	while (first != last)
	{
		_con.push_back(*first);
		++first;
		
		//建堆
		for (int i = (_con.size() - 1 - 1) / 2; i >= 0; i--)
		{
			AdjustDown(i);
		}
	}
}

2.2 建堆

向下调整的时间复杂度是O(N)，向上调整的时间复杂度是O(N*logN)，所以采用向下调整建堆

详细讲解可查看：数据结构——二叉树(堆、堆排序、二叉树链式结构)

向下调整

//向下调整 默认大堆
void AdjustDown(int parent)
{
	int child = parent * 2 + 1;
	while (child < _con.size())
	{
		if (child + 1 < _con.size() && _con[child + 1] > _con[child])
		{
			child = child + 1;
		}
		if (_con[child] > _con[parent])
		{
			std::swap(_con[child], _con[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

向上调整

//向上调整
void AdjustUp(int child)
{
	int parent = (child - 1) / 2;

	while (child > 0)
	{
		if (_con[child] > _con[parent])
		{
			std::swap(_con[child], _con[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

2.3 仿函数

STL的priority_queue默认是大堆，如果想要指定小堆，则需要在参数列表里面指定参数

std::priority_queue<int> maxHeap;  // 默认：大堆
std::priority_queue<int, std::vector<int>, std::greater<int>> minHeap;	//小堆

这里我们要实现，就要用到仿函数

仿函数是一个类，它重载了函数调用运算符operator()，这使得这个类就可以想函数一样被调用

在这里我们就重载operator()来模拟比较函数

template<class T>
class Less
{
public:
	bool operator()(const T& x, const T& y)
	{
		return x < y;
	}

};

template<class T>
class Greater
{
public:
	bool operator()(const T& x, const T& y)
	{
		return x > y;
	}

};

priority_queue不指定的情况下，默认是大堆，指定模板时将Less设为缺省参数即可

template<class T, class Container = vector<T>, class Compare = Less<T>>
class priority_queue

有了仿函数，我们的向下调整和向上调整在选择建大堆或者小堆的时候，调用这个仿函数即可：

//向下调整 默认大堆
void AdjustDown(int parent)
{
	Compare com;
	int child = parent * 2 + 1;
	while (child < _con.size())
	{
		//if (child + 1 < _con.size() && _con[child + 1] > _con[child])
		if (child + 1 < _con.size() && com(_con[child], _con[child + 1]))
		{
			child = child + 1;
		}
		//if (_con[child] > _con[parent])
		if (com(_con[parent], _con[child]))
		{
			std::swap(_con[child], _con[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
//向上调整
void AdjustUp(int child)
{
	Compare com;
	int parent = (child - 1) / 2;

	while (child > 0)
	{
		//if (_con[child] > _con[parent])
		if (com(_con[parent], _con[child]))
		{
			std::swap(_con[child], _con[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

2.4 push & pop操作

• 插入操作即在队尾增加一个元素，然后向上调整，保证这还是一个堆

• 删除操作还是模拟堆的操作，将首元素和最后一个元素交换，然后删除队尾元素

  这样保证了即使删除之后，下面的还是一个堆，接下来向下调整即可

void pop()
{
	std::swap(_con[0], _con[_con.size() - 1]);
	_con.pop_back();
	AdjustDown(0);
}
void push(const T& x)
{
	_con.push_back(x);
	AdjustUp(_con.size() - 1);
}

2.5 top & empty & size

这empty和size直接调用vector的接口即可；top查看队头元素，返回队头元素即可

const T& top() const
{
	return _con[0];
}
bool empty() const
{
	return _con.empty();
}
size_t size()
{
	return _con.size();
}

---

那本期的分享就到这咯，我们下期再见，如果还有下期的话