【NLP】深入浅出全面回顾注意力机制
深入浅出全面回顾注意力机制
- 1. 注意力机制概述
- 2. 举个例子:使用PyTorch带注意力机制的Encoder-Decoder模型
- 3. Transformer架构回顾
-
- 3.1 Transformer的顶层设计
- 3.2 Encoder与Decoder的输入
- 3.3 高并发长记忆的实现
-
- self-attention的矩阵计算形式
- 多头注意力(Multi-Head Attention)机制
- 3.4 为加深Transformer网络层的几种方法
- 3.5 如何自监督学习?
- 相关资料
之前的博文已经学习过注意力机制,今天我们重新回顾一下。理解注意力机制是学会Transformer的基石,例如Seq2Seq引入注意力机制、Transformer使用自注意力机制(self-Attention Mechanism),使得NLP、推荐系统等方面取得了新的突破。
1. 注意力机制概述
注意力指人可以关注一些信息的同时忽略其他信息的选择能力。根据注意力范围的不同,分为软注意力和硬注意力:
软注意力(soft attention)。比较常见,对所有key求权重概率,每个key都有一个对应的权重,是一种全局的计算方式(也叫做Global Attention)。这种方式比较理性,参考了所有key的内容,再进行加权,但是计算量会比较大。硬注意力(hard attention)。该方式直接精确定位到某个key,而忽略其余所有key,相当于这个key的概率是1,其余key的概率全部是0。因此这种对齐方式要求很高。
在NLP应用中会把注意力机制看作输出(Target)句子中某个单词和输入(Source)句子每个单词的相关性。目标句子生成的每个单词对应输入句子单词的概率分布可以理解为输入句子的单词和这个目标生成的单词的对齐概率。
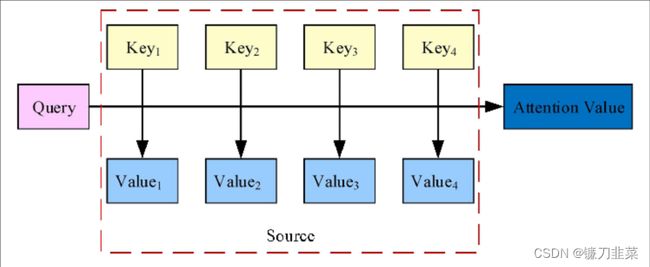
图1 注意力机制的实质
在上图中,Source由一系列
那么该如何计算注意力呢?计算过程分为3个阶段:
- 根据Query和Key计算两者的相似性或者相关性,常见的计算方式包括①求两者的向量点积、②求两者的向量Cosine相似性或者③通过再引入额外的神经网络来求,假设求得得相似值为 s i s_i si。
- 对第1阶段的值进行归一化处理,得到权重系数,这里使用Softmax函数计算各权重的值( a i a_i ai),计算公式为 a i = S o f t m a x ( s i ) = e s i ∑ J = 1 T e s J a_i=Softmax(s_i)=\frac{e^{s_i}}{\sum_{J=1}^T {e^{s_J}}} ai=Softmax(si)=∑J=1TesJesi
- 使用第2阶段的权重系数对Value进行加权求和。 A t t e n t i o n ( Q u e r y , S o u r c e ) = ∑ i = 1 T a i ⋅ V a l u e i Attention(Query, Source)=\sum_{i=1}^T {a_i \cdot Value_i} Attention(Query,Source)=i=1∑Tai⋅Valuei
2. 举个例子:使用PyTorch带注意力机制的Encoder-Decoder模型
(1)构建Encoder
使用PyTorch构建Encoder把输入句子中的每个单词用torch.nn.Embedding(m,n)转换为词向量,然后通过一个编码器(这里采用GRU模型),对于每个输入字,输出向量和隐藏状态,并将隐藏状态用于下一个输入字。
class EncoderRNN(nn.Module):
"""
构建Encoder
"""
def __init__(self, input_size, hidden_size):
super(EncoderRNN, self).__init__()
self.hidden_size = hidden_size
self.embedding = nn.Embedding(input_size, hidden_size)
self.gru = nn.GRU(hidden_size, hidden_size)
def forward(self, input, hidden):
embedded = self.embedding(input).view(1, 1, -1)
output = embedded
output, hidden = self.gru(output, hidden)
return output, hidden
def initHidden(self):
return torch.zeros(1, 1, self.hidden_size, device=device)
(2)构建简单Decoder
先构建一个简单的解码器,这个解码器只使用编码器的最后输出。这最后一个输出有时称为上下文向量,因为它从整个序列中编码上下文。该上下文向量用作解码器的初始隐藏状态。在解码的每一步,解码器都被赋予一个输入指令和隐藏状态. 初始输入指令字符串开始的指令,第一个隐藏状态是上下文向量(编码器的最后隐藏状态)
class DecoderRNN(nn.Module):
def __init__(self, hidden_size, output_size):
super(DecoderRNN, self).__init__()
self.hidden_size = hidden_size
self.embedding = nn.Embedding(output_size, hidden_size)
self.gru = nn.GRU(hidden_size, hidden_size)
self.out = nn.Linear(hidden_size, output_size)
self.softmax = nn.LogSoftmax(dim=1)
def forward(self, input, hidden):
output = self.embedding(input).view(1,1,-1)
output = F.relu(output)
output, hidden = self.gru(output, hidden)
output = self.softmax(self.out(output[0]))
return output, hidden
def initHidden(self):
return torch.zeros(1, 1, self.hidden_size, device=device)
(3)构建注意力Decoder
以典型的Bahanau注意力架构为例,主要有四层。嵌入层讲输入字转换为矢量,计算每个编码器输出的注意能量的层、RNN层和输出层。解码器的输入包括循环网络最后的隐含状态 s i − 1 s_{i-1} si−1、最后输出 y i − 1 y_{i-1} yi−1,所有的编码器的所有输出 h ∗ h_* h∗。
- 这些输入,分别通过不同的层接受, y t − 1 y_{t-1} yt−1作为嵌入层的输入。
embedded = embedding(last_rnn_output)
- 注意力层的函数 a a a的输入为 s t − 1 s_{t-1} st−1和 h j h_j hj,输出为 e t j e_{tj} etj,标准化处理后为 α t j \alpha_{tj} αtj
attn_energies[j] = attn_layer(last_hidden, encoder_outputs[j])
attn_weights = normalize(attn_energies)
- 向量 C t C_t Ct为编码器各输出的注意力加权平均。
context = sum(attn_weights * encoder_outputs)
- 循环层 f f f的输入为 ( s t − 1 , y t − 1 , c t ) (s_{t-1},y_{t-1}, c_t) (st−1,yt−1,ct),输出为内部隐含状态及 s t s_t st。
rnn_input = concat(embedded, context)
rnn_output, rnn_hidden = rnn(rnn_input, last_hidden)
- 输出层 g g g的输入为 ( y i − 1 , s i , c i ) (y_{i-1},s_{i},c_{i}) (yi−1,si,ci),输出为 y i y_i yi。
output = out(embedded, rnn_output, context)
- 综合以上各步,即可得到Bahdanau注意力的解码器。
class BahdanauAttnDecoderRNN(nn.Module):
def __init__(self, hidden_size, output_size, n_layers=1, dropout_p=0.1):
super(AttnDecoderRNN, self).__init__()
# 定义参数
self.hidden_size = hidden_size
self.output_size = output_size
self.n_layers = n_layers
self.dropout_p = dropout_p
self.max_length = max_length
# 定义层
self.embedding = nn.Embedding(output_size, hidden_size)
self.dropout = nn.Dropout(dropout_p)
self.attn = GeneralAttn(hidden_size)
self.gru = nn.GRU(hidden_size * 2, hidden_size, n_layers, dropout=dropout_p)
self.out = nn.Linear(hidden_size, output_size)
def forward(self, word_input, last_hidden, encoder_outputs):
# 前向传播每次运行一个时间步,但使用使用所有的编码器输出
# 获取当前词嵌入 (last output word)
word_embedded = self.embedding(word_input).view(1, 1, -1) # S=1 x B x N
word_embedded = self.dropout(word_embedded)
# 计算注意力权重并使用编码器输出
attn_weights = self.attn(last_hidden[-1], encoder_outputs)
context = attn_weights.bmm(encoder_outputs.transpose(0, 1)) # B x 1 x N
# 把词嵌入与注意力context结合在一起,然后传入循环网络
rnn_input = torch.cat((word_embedded, context), 2)
output, hidden = self.gru(rnn_input, last_hidden)
# 定义最后输出层
output = output.squeeze(0) # B x N
output = F.log_softmax(self.out(torch.cat((output, context), 1)))
# 返回最后输出,隐含状态及注意力权重
return output, hidden, attn_weights
3. Transformer架构回顾
3.1 Transformer的顶层设计
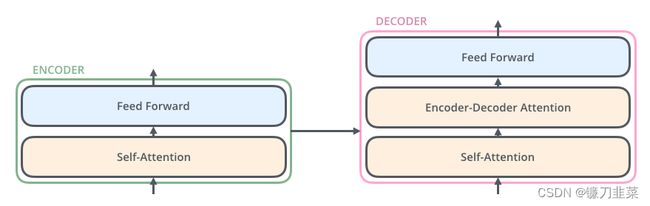
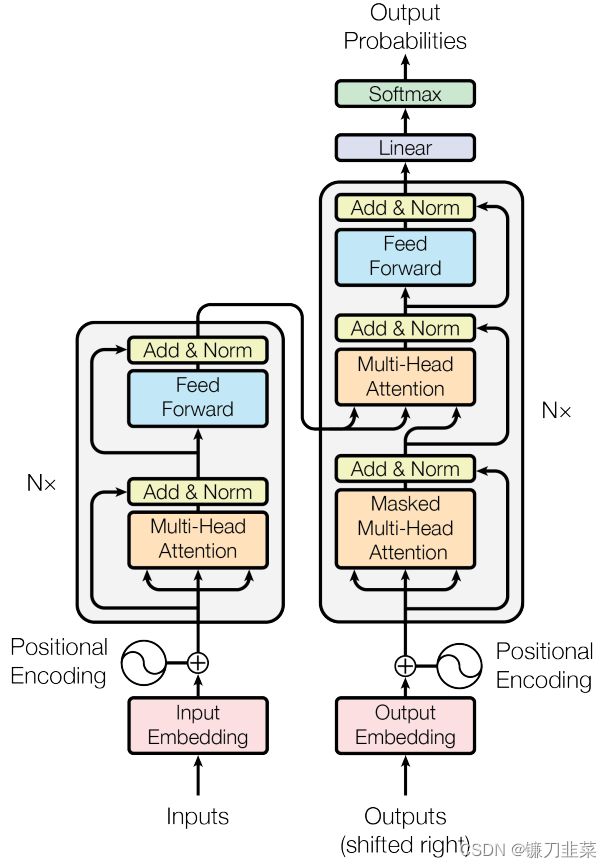
Transformer是一个由编码器和解码器构成的网络结构。其Encoder组件由6个相同结构的Encoder串联而成,Decoder组件也是由6个结构相同的Decoder串联而成。如下所示

最后一层Encoder的输出将传入Decoder的每一层。进一步打开Encoder及Decoder会发现,每个编码器由一层自注意力和一层前馈网络构成,而解码器初自注意力层、前馈层外,中间还有一个用来接收最后一个编码器的输出值,如下所示
3.2 Encoder与Decoder的输入
如何解决语句中各单词的次序或位置关系问题呢?Transformer使用位置编码(Position Encoding)来记录各单词在语句中的位置或次序,位置编码的值遵循一定规则(如由三角函数生成),每个源单词(或目标单词)的词嵌入与对应的位置编码相加(位置编码向量与词嵌入的维度相同),如下图所示

对解码器的输入(即目标数据)也需要做同样处理,即目标数据加上位置编码成为带有时间信息的嵌入。当对语料库进行批量处理时,可能会遇到长度不一致的语句:对于短的语句,可以用填充(如用0填充)的方式补齐;对于太长的语句,可以采用截尾的方法对齐(如给这些位置的值赋一个很大的负数,使之在进行Softmax运算时为0).
3.3 高并发长记忆的实现
Transformer采用自注意力机制实现。与一般注意力机制不同在于Query的来源不同,一般注意力机制中的query来源于目标语句(而非源语句),而自注意力机制的query来源于源语句本身(而非目标语句,如翻译后的语句)。

Encoder模块中自注意力机制的主要计算步骤如下(与Decoder模块的自注意力机制类似):
1)把输入单词转换为带时间(或时序)信息的嵌入向量。
2)根据嵌入向量生成q、k、v三个向量,这三个向量分别表示query、key、value。
3)根据q,计算每个单词点积后的得分:score=q·k。
4)对score进行规范化、softmax处理,假设结果为a。
5)a与对应的v相乘,然后累加得到当前语句各单词之间的自注意力z: z = ∑ a v z=\sum av z=∑av。
计算自注意力的第一步是根据编码器的每个输入向量创建三个向量(在这种情况下,是每个单词的嵌入)。因此,我们为每个单词创建一个Query向量、一个Key向量和一个Value向量。这些向量是通过将embedding 乘以我们在训练过程中训练的三个矩阵来创建的。
请注意,这些新向量的维度比embedding向量小。它们的维度为64,而embedding和encoder的输入/输出向量的维度为512。它们不必较小,这是对计算多头注意(主要)常数计算的架构选择。

将x1乘以 W Q W_Q WQ权重矩阵得到 q 1 q_1 q1,即与该单词相关联的“query”向量。我们最终为输入句子中的每个单词创建了一个“query”、一个“key”和一个“value”映射。
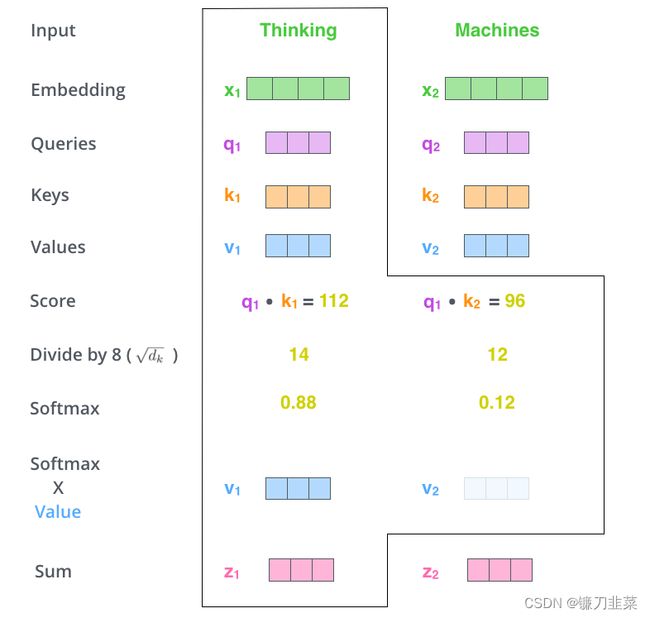
什么是“query”、“key”和“value”向量?它们是对计算和思考注意力很有用的抽象概念。计算自注意力的第二步是计算一个分数。假设当前带翻译的语句为:Thinking Machines。单词Thinking的预处理(即词嵌入+位置编码得到嵌入向量Embedding)后用 x 1 x_1 x1表示,单词Machines预处理后用 x 2 x_2 x2表示。计算单词Thinking与当前语句中各单词的注意力得分(score),如下:
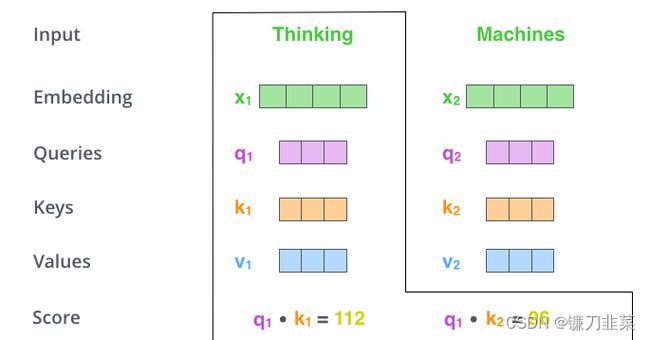
假设各嵌入向量的维度为 d m o d e l d_{model} dmodel(这个值一般较大,如为512),在上图中q、k、v的维度比较小,一般使q、k、v的维度满足: d q = d k = d v = d m o d e l h d_q=d_k=d_v=\frac{d_{model}}{h} dq=dk=dv=hdmodel(h表示h个head)。
第三步和第四步是将分数除以8(论文中使用的关键向量的维数的平方根–64)。这导致具有更稳定的梯度。这里可能有其他可能的值,但这是默认值),然后通过softmax操作传递结果。Softmax将分数标准化,使其全部为正,加起来为1。
考虑到实际计算过程中得到的score可能比较大,为了保证计算梯度时不影响其稳定性,需要进行归一化操作,这里除以 d k \sqrt{d_k} dk,如下所示 :
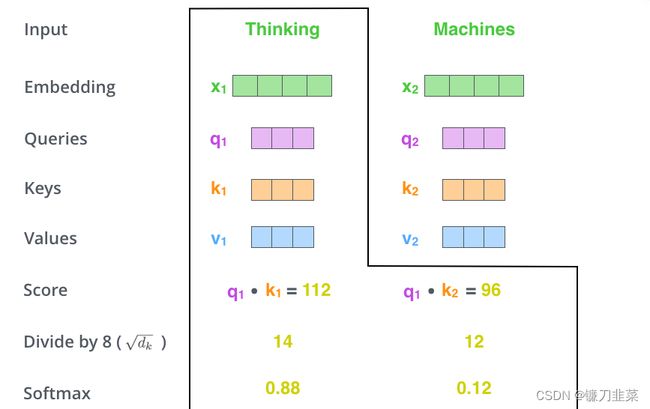
这个softmax分数决定了每个单词在这个位置上的表达量。显然,这个位置的单词将具有最高的softmax分数,但有时关注与当前单词相关的另一个单词是有用的。
对归一化处理后的 a a a与 v v v相乘再累加,就得到 z z z,如下所示:
第五步是将每个值向量乘以softmax分数(准备将它们相加)。这里的直觉是保持我们想要关注的单词的值不变,并淹没不相关的单词(例如,将它们乘以0.001等微小数字)。
第六步是对加权值向量求和。这就在这个位置产生了自注意层的输出(对于第一个单词)。
自注意力的计算到此结束。得到的向量是我们可以发送到前馈神经网络的向量。然而,在实际实现中,这种计算是以矩阵形式进行的,以便更快地进行处理。现在让我们来看看,我们已经看到了单词水平上计算的直觉。
self-attention的矩阵计算形式
第一步是计算Query、Key和Value矩阵。我们通过将embeddings打包到矩阵X中,并将其乘以我们训练的权重矩阵(WQ、WK、WV)来实现这一点。

X矩阵中的每一行对应于输入句子中的一个单词。我们再次看到embedding向量(512个,或图中的4个框)和q/k/v向量(64个,或图中的3个框)的大小差异
最后,由于我们处理的是矩阵,可以将第二步到第六步浓缩为一个公式来计算自注意层的输出。
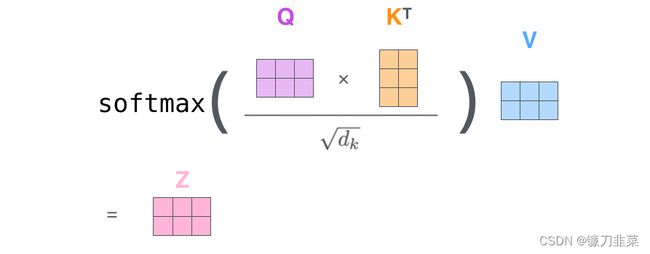
整个计算过程也可以使用下图表示,这个 z z z又称为缩放点积注意力(Scaled Dot-Product Attention)。
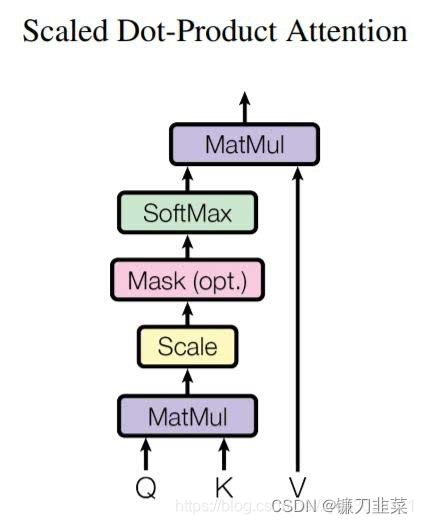
其中MatMul表示点积运算,Mash表示掩码,用于遮掩某些值,使其在参数更新时不产生效果。
在Transformer模型中,Scaled Dot-Product Attention被用于实现Multi-Head Attention。具体来说,Multi-Head Attention将输入矩阵分别进行多个头的线性变换,然后对每个头的变换结果分别计算Scaled Dot-Product Attention,最后将每个头的Attention结果拼接在一起并通过一个线性变换输出。Scaled Dot-Product Attention的计算方式如下:
- 计算Query矩阵Q、Key矩阵K的乘积,得到得分矩阵scores。
- 对得分矩阵scores进行缩放,即将其除以向量维度的平方根(np.sqrt(d_k))。
- 若存在Attention Mask,则将Attention Mask的值为True的位置对应的得分矩阵元素置为负无穷(-inf)。
- 对得分矩阵scores进行softmax计算,得到Attention权重矩阵attn。
- 计算Value矩阵V和Attention权重矩阵attn的乘积,得到加权后的Context矩阵。
缩放点积注意力的代码:
class ScaledDotProductAttention(nn.Module):
def __init__(self, mask_value=-1e9):
super(ScaledDotProductAttention, self).__init__()
self.mask_value = mask_value
def forward(self, Q, K, V, attn_mask=None):
'''
Q: [batch_size, n_heads, len_q, d_k]
K: [batch_size, n_heads, len_k, d_k]
V: [batch_size, n_heads, len_v(=len_k), d_v]
attn_mask: [batch_size, n_heads, seq_len, seq_len]
'''
d_k = Q.size(-1)
scores = torch.matmul(Q, K.transpose(-1, -2)) / np.sqrt(d_k) # scores : [batch_size, n_heads, len_q, len_k]
if attn_mask is not None:
scores.masked_fill_(attn_mask, self.mask_value)
attn = nn.Softmax(dim=-1)(scores)
context = torch.matmul(attn, V) # [batch_size, n_heads, len_q, d_v]
return context, attn
核心代码是这一句:
scores = torch.matmul(Q, K.transpose(-1, -2)) / np.sqrt(d_k)
将scores除以d_k的平方根(np.sqrt(d_k)),这就是所谓的缩放,可以避免得分过大或过小。
通过这种方式,Scaled Dot-Product Attention可以计算出Query和Key之间的相似度,同时考虑了Value矩阵对最终结果的影响,进而实现了注意力机制的作用。
Transformer模型涉及两种掩码方式,分别时Padding Mask(填充掩码)和Sequence Mask(序列掩码).Padding Mask会用在所有的缩放点积注意力中,用于处理长短不一的语句;而Sequence Mask只会用在Decoder的自注意力中,用于防止Decoder预测目标值时看到未来的值。
(1)Padding Mask
什么是Padding Mask呢?因为每个批次输入序列长度是不一样的,也就是说,要对输入序列进行对齐。具体来说,就是给在较短的序列后面填充 0。如果输入的序列太长,则截取左边的内容,把多余的直接舍弃。因为这些填充的位置,其实是没什么意义的,所以Attention 机制不应该把注意力放在这些位置上,所以我们需要进行一些处理。
具体的做法是,给这些位置的值加上一个非常大的负数(负无穷),这样的话,经过Softmax,这些位置的概率就会接近0!而Padding Mask 实际上是一个张量,每个值都是一个 Boolean,值为 false 的地方就是我们要进行处理的地方。
def padding_mask(seq_k, seq_q):
# seq_k 和 seq_q 的形状都是 [B,L]
len_q = seq_q.size(1)
# `PAD` is 0
pad_mask = seq_k.eq(0)
pad_mask = pad_mask.unsqueeze(1).expand(-1, len_q, -1) # shape [B, L_q, L_k]
return pad_mask
(2)Sequence Mask
前面也提到,Sequence Mask 是为了使得Decoder不能看见未来的信息。也就是说,对于一个序列,在time_step 为 t 的时刻,解码输出应该只能依赖于 t 时刻之前的输出,而不能依赖 t 之后的输出。因此需要想一个办法,把 t 之后的信息给隐藏起来。
那么具体怎么做呢?也很简单:产生一个上三角矩阵,上三角的值全为 1,下三角的值全为0,对角线也是 0。然后让序列乘以这个矩阵,即把这个矩阵作用在每一个序列上,就可以达到目的。
def sequence_mask(seq):
batch_size, seq_len = seq.size()
mask = torch.triu(torch.ones((seq_len, seq_len), dtype=torch.uint8),
diagonal=1)
mask = mask.unsqueeze(0).expand(batch_size, -1, -1) # [B, L, L]
return mask
对于Decoder的自注意力,里面使用到的缩放点积注意力,同时需要Padding Mask和Sequence Mask作为attn_mask、具体实现时需要将两个Mask相加作为attn_mask。其他情况,attn_mask一律等于Padding Mask。
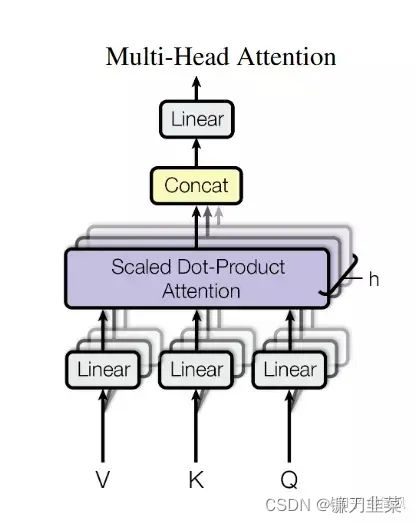
多头注意力(Multi-Head Attention)机制
多头注意力机制可以从3个方面提升注意力层的性能。
1)它扩展了模型专注于于不同位置的能力。
2)将缩放点积注意力过程做 h h h次,再把输出合并起来。
3)它为注意力层(Attention Layer)提供了多个“表示子空间”。
在多头注意力结构中,正如接下来将看到的,我们不仅有一组,还有多组查询/键/值权重矩阵(Transformer使用八个注意力头,因此最终为每个编码器/解码器提供八组)。这些集合中的每一个都是随机初始化的。然后,在训练之后,利用集合将输入嵌入(Input Embedding)(或来自较低编码器/解码器的向量)投影到不同的表示子空间中。其原理实现与使用不同卷积核把源图像投影到不同风格的子空间一样。
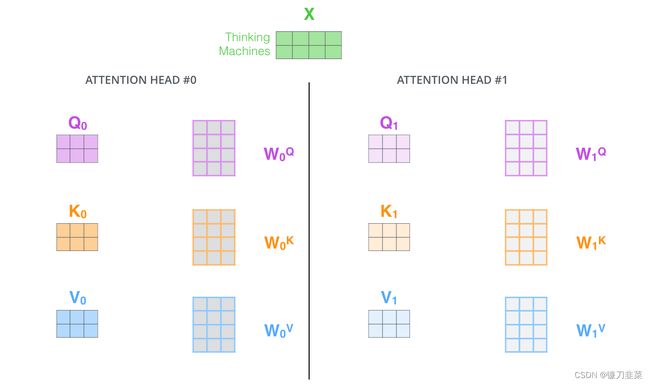
对于多头注意力,为每个头保持单独的Q/K/V权重矩阵,从而产生不同的Q/K/V矩阵。正如之前所做的,将X乘以 W Q W_Q WQ/ W K W_K WK/ W V W_V WV矩阵,得到Q/K/V矩阵。
Multi-Head Attention 的结构图如下所示:
如果进行与上面概述的相同的自注意计算,只是用不同的权重矩阵进行八次不同的计算,最终得到八个不同的Z矩阵
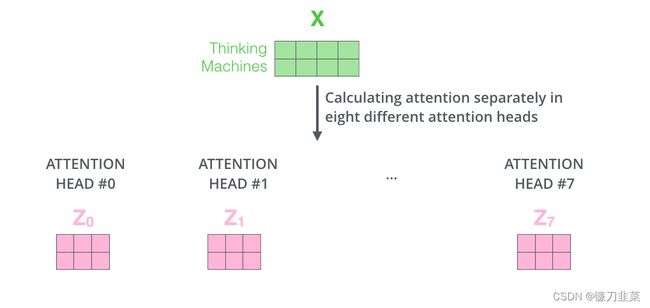 这给我们留下了一点挑战。前馈层不需要八个矩阵,而是需要一个矩阵(每个单词一个向量)。所以需要一种方法把这八个元素浓缩成一个矩阵。
这给我们留下了一点挑战。前馈层不需要八个矩阵,而是需要一个矩阵(每个单词一个向量)。所以需要一种方法把这八个元素浓缩成一个矩阵。
该怎么做呢?将矩阵连接起来,然后将它们乘以额外的权重矩阵 W O W_O WO。

多头注意力机制的运算过程如下:
- 随机初始化八组矩阵,KaTeX parse error: Undefined control sequence: \0 at position 49: …es 64}, i\in \{\̲0̲,1,2,3,4,5,6,7};
- 使用X与这八组矩阵相乘,得到八组 Q i , K i , V i ∈ R 512 , i ∈ { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 } Q_i,K_i,V_i\in R^{512}, i\in \{0,1,2,3,4,5,6,7\} Qi,Ki,Vi∈R512,i∈{0,1,2,3,4,5,6,7};
- 由此得到八个 Z i , i ∈ { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 } Z_i, i\in \{0,1,2,3,4,5,6,7\} Zi,i∈{0,1,2,3,4,5,6,7},然后把这八个 Z i Z_i Zi组合成一个大的 Z 0 ∼ 7 Z_{0\sim 7} Z0∼7;
- Z Z Z与初始化的矩阵 W 0 ∈ R 512 × 512 W^0\in R^{512\times 512} W0∈R512×512相乘,得到最终输出值 Z Z Z。
具体运算过程如下图所示:

由之前的内容可知,解码器比编码器中多了编码器与解码器注意力层(Encoder-Decoder Attention Layer)。在编码器与解码器注意力层中, Q Q Q来自解码器的上一个输出, K K K和 V V V则来自编码器最后一层的输出,其计算过程与自注意力相同。
例如在机器翻译中,解码过程是一个顺序操作的过程,也就是当解码第k个特征向量时,只能看到第 k − 1 k-1 k−1及其之前的解码结果,这种情况下的多头注意力叫做掩码多头注意力(Masked Multi-Head Attention),即同时使用了Padding Mask和Sequence Mask两种方法。
基于以上分析,自注意力机制没有前后依赖关系,可以基于矩阵进行高并发处理,另外每个单词的输出与前一层各单词的距离都为1,说明不存在梯度随着长距离而消失的问题,因此Transformer就有了高并发和长记忆的强大功能!
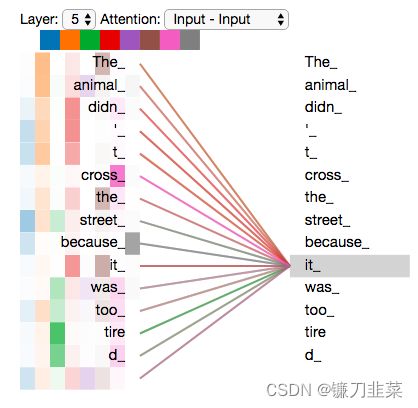
每个单词的输出与前一层各单词的距离都为1。
Multi-Head Attention 实现:
class MultiHeadAttention(nn.Module):
def __init__(self, model_dim=512, num_heads=8, dropout=0.0):
super(MultiHeadAttention, self).__init__()
self.dim_per_head = model_dim // num_heads
self.num_heads = num_heads
self.linear_k = nn.Linear(model_dim, self.dim_per_head * num_heads)
self.linear_v = nn.Linear(model_dim, self.dim_per_head * num_heads)
self.linear_q = nn.Linear(model_dim, self.dim_per_head * num_heads)
self.dot_product_attention = ScaledDotProductAttention(dropout)
self.linear_final = nn.Linear(model_dim, model_dim)
self.dropout = nn.Dropout(dropout)
# multi-head attention之后需要做layer norm
self.layer_norm = nn.LayerNorm(model_dim)
def forward(self, key, value, query, attn_mask=None):
# 残差连接
residual = query
dim_per_head = self.dim_per_head
num_heads = self.num_heads
batch_size = key.size(0)
# linear projection
key = self.linear_k(key)
value = self.linear_v(value)
query = self.linear_q(query)
# split by heads
key = key.view(batch_size * num_heads, -1, dim_per_head)
value = value.view(batch_size * num_heads, -1, dim_per_head)
query = query.view(batch_size * num_heads, -1, dim_per_head)
if attn_mask:
attn_mask = attn_mask.repeat(num_heads, 1, 1)
# scaled dot product attention
scale = (key.size(-1)) ** -0.5
context, attention = self.dot_product_attention(
query, key, value, scale, attn_mask)
# concat heads
context = context.view(batch_size, -1, dim_per_head * num_heads)
# final linear projection
output = self.linear_final(context)
# dropout
output = self.dropout(output)
# add residual and norm layer
output = self.layer_norm(residual + output)
return output, attention
3.4 为加深Transformer网络层的几种方法
Transformer采用了两种方法:一种是残差连接(Residual Connection),另一种是归一化(Normalization)。具体实现方法
就是在每个编码器或解码器的两个子层(即Self-Attention和FFNN(Feed Forward Neural Network, 前馈神经网络))间增加由残差连接和归一化组成的层,如下所示:

每个编码器中的每个子层(self-attention,FFNN)周围都有一个残差连接,然后是一个layer-normalization步骤。如果要可视化向量和与自注意相关的层范数运算,它看起来是这样的:
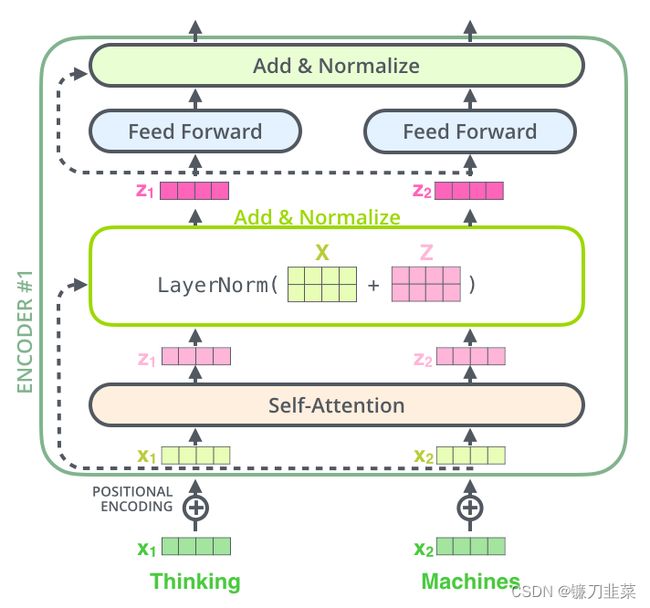
这也适用于解码器的子层。如果考虑一个由2个堆叠编码器和解码器组成的Transformer,它看起来像这样:

至此,我们已经回顾了编码器的大多数概念,也基本上知道解码器组件如何工作。让我们看一下它们如何一起工作:编码器从处理输入序列开始。然后将top encoder的输出转换为一组attention向量K和V。这些将由每个decoder在其“encoder-decoder attention”层中使用,这有助于解码器将注意力集中在输入序列中的适当位置:
在完成编码阶段之后,开始解码阶段。解码阶段的每个步骤都从输出序列中输出一个元素(在这种情况下是英语翻译句子)。
3.5 如何自监督学习?
Encoder最后的输出通过一个全连接层及Softmax函数作用后就得到了预测值的对数概率(这里假设采用贪婪编码的方法,即用argmax函数获取概率最大值对应的索引),如下图所示。预测值的对数概率与实际值对应的独热编码的差就构成模型的损失函数。
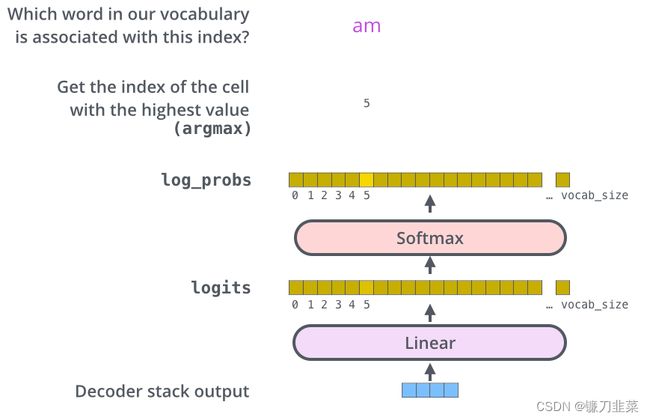
Transformer的最后全连接层及Softmax函数。
综上所述,Transformer模型由Encoder和Decoder组件构成,每个Encoder组件又由6个Encoder层组成,每个Encoder层包含一个自注意力子层和一个全连接子层;而Decoder组件也是由6个Decoder层组成,每个Decoder层包含一个自注意力子层、注意力子层和全连接子层。
相关资料
- Understanding Transformer Neural Network Model in Deep Learning and NLP
- The Illustrated Transformer
- 六种位置编码的代码实现及性能实验
- 聊聊 Transformer
