Python 中的提升算法
什么是提升
我们将使用称为 *Boosting* 的算法结束树章节。除了随机森林,*Boosting* 是另一种增强经典决策和回归树模型预测能力的强大方法。Boosting 算法本身严格来说既不能学习也不能预测任何东西,因为它是建立在其他(弱)算法之上的。Boosting 算法被称为“元算法”。Boosting 方法(以及 bootstrapping 方法)原则上可以应用于任何分类或回归算法,但结果证明树模型特别适合。事实证明,提升树的准确性与随机森林相当,甚至常常优于后者(参见例如 Caruana 和 Niculescu-Mizil (2008)(*监督学习算法的实证比较*))。哈斯蒂等人。(2009) 将提升决策树称为“世界上最好的现成分类器”(Hastie 等人,2006 p.340)。Boosting 背后的奥秘在原则上与随机森林模型相同 * - 一组比随机猜测稍好一些的弱学习器可以组合起来做出比一个强学习器更好的预测 - *。但是,这些弱学习器的创建过程是不同的。Boosting 背后的奥秘在原则上与随机森林模型相同 * - 一组比随机猜测稍好一些的弱学习器可以组合起来做出比一个强学习器更好的预测 - *。但是,这些弱学习器的创建过程是不同的。Boosting 背后的奥秘在原则上与随机森林模型相同 * - 一组比随机猜测稍好一些的弱学习器可以组合起来做出比一个强学习器更好的预测 - *。但是,这些弱学习器的创建过程是不同的。
回顾一下,在创建我们的随机森林模型期间,我们使用了 Bagging 的概念。在 Bagging 期间,我们种植了许多 *M* 棵树,其中每棵树都建立在原始数据集的随机样本(允许重新采样)上,其中随机样本的长度与原始数据集的长度相同,但仅包含总数的一个随机抽取的子集特征空间。在我们创建了这些模型之后,我们让他们以多数票来做出我们的最终决定。精髓是每个树模型的创建都独立于其他树模型的结果。也就是说,树模型的“形状”仅受基础数据的“形状”影响,而基础数据的“形状”仅受偶然性(*采样和重采样*)的影响。n吨H* 树依赖于先前创建的返回结果 (n吨H-1) 树模型。
因此,与我们并行创建树模型集合的随机森林方法不同,我们现在按顺序创建集合,其中实际树的设置受到所有先前树模型的输出的影响,通过改变权重的数据集,树模型是建立在。关键是,通过实现这些权重,我们引入了某种学习,其中 *n吨H* 提升模型中的树部分取决于预测 *n吨H-1* 模型已作出。因此,我们在引导过程中或多或少地用“引导”创建替换了单个数据集的“随机引导”创建。最著名的提升算法称为 *AdaBoost*(自适应提升),由 Freund 和 Schapire (1996) 开发。以下讨论基于 AdaBoost Boosting 算法。下图提供了对 boosting 算法的直观了解。
这里不同的基分类器每个都建立在加权数据集上,其中数据集中单个实例的权重取决于先前基分类器为这些实例所做的结果。如果他们对实例进行了错误分类,则该实例的权重将在下一个模型中增加,而如果分类正确,则权重保持不变。最终决策是通过基本分类器的加权投票来实现的,其中权重取决于模型的错误分类率。如果一个模型的分类准确率很高,它就会得到很高的权重,而如果分类准确率很差,它就会得到低权重。
提升伪代码
将所有权重初始化为 瓦=1n 在哪里 n 是数据集中的实例数
- 尽管 吨 < 吨 (吨==要培养的模型数量)做:
- 创建模型并得到假设 H吨(Xn) 对于所有数据点 Xn 在数据集中
- 计算误差 ε 对所有数据点求和的训练集 Xn 在训练集中:
ε吨 = ∑n=1N瓦n(吨)*一世(是n≠H吨(Xn))∑n=1N瓦n(吨)
在哪里 一世(C○nd) 返回 1 如果 一世(C○nd) == 真,否则为 0
- 计算 α 和:
α吨 = 日志(1-ε吨ε吨)
- 更新权重 N 接下来的训练实例(吨+1) 模型:
瓦n(吨+1) = 瓦n(吨)*电子Xp(α吨*一世(是n≠H吨(Xn)))
- 之后 吨 迭代,计算最终输出:
F(X) = 秒一世Gn(∑吨吨α吨*H吨(X))
使用 Python 从头开始提升
在之前关于分类树、回归树 和随机森林模型的章节中,我们一直拖着整个“从头开始的树代码”。我想我们现在已经理解了如何在 Python 中从头开始构建树模型(用于回归或分类)的概念,如果没有,只需转到前面的一章并使用代码!由于 Boosting 概念的威力和神秘性更多地在于弱学习器的组合,因为在创建这些弱学习器时,我们将使用sklearn 的 DecisionTreeClassifier 来创建单个弱学习器,但将从头开始编写实际的 boosting 过程。
为了使 sklearn DecisionTreeClassifier 成为*弱*分类器,我们将设置 *max_depth* 参数 == 1 以创建称为 *decision Stump* 的东西,它在原则上(如上所述)没有别的东西作为只有一层的决策树,即也就是说,根节点直接以叶节点结束,因此数据集只分裂一次。与往常一样,我们将使用香农熵作为分割标准。
正如您可能看到的,即使我们在这里不使用我们的自编码决策树算法,我们在实际的树构建算法中唯一必须改变的是我们引入了一个最大深度参数,该参数在第一次分裂后停止生长树 -代码中的这种细微变化实际上不值得拖到这里 - 作为数据集,我们使用UCI 蘑菇数据集, 就像我们在之前的随机森林章节中所做的那样。
让我们首先创建一个决策树桩并测量该决策树桩的准确性,以了解该模型的预测“好”或更“坏”。
"""
创建一个决策树桩
"""
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from matplotlib import style
style 。使用( 'fivethirtyeight' )
from sklearn.tree import DecisionTreeClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import cross_validate
import scipy.stats as sps
# 加载数据并定义列标签
数据集 = pd 。read_csv ( 'data\mushroom.csv' , header = None )
dataset = dataset 。样本( frac = 1 )
数据集。列 = [ '目标' , '帽形状' , '帽表面' , '帽颜色' , '瘀伤' , '气味' , '鳃附件' , '鳃间距' ,
'鳃大小' , '鳃色' ,, 'stalk-root' , 'stalk-surface-above-ring' , 'stalk-surface-below-ring' , 'stalk-color-above-ring' ,
'stalk-color-below-ring' , 'veil-类型' ,'面纱颜色' ,'环号' ,'环类型' ,'孢子打印颜色' ,'人口' ,
'栖息地' ]
#编码从字符串到整数的特征值,因为sklearn DecisionTreeClassifier只需数值
为 标签 的 数据集。列:
数据集[标签] = LabelEncoder () 。适合(数据集[标签])。变换(数据集[标签])
Tree_model = DecisionTreeClassifier (标准= "entropy" , max_depth = 1 )
X = 数据集。drop ( 'target' , axis = 1 )
Y = dataset [ 'target' ] 。其中(数据集[ '目标' ] == 1 ,- 1 )
预测 = np 。均值( cross_validate ( Tree_model , X , Y , cv = 100 )[ 'test_score' ])
打印('准确度为:' ,预测* 100 ,'%' )
输出:
准确率为:73.06860322953968%
请注意,我们已经使用 100 倍交叉验证在同一数据集(整个数据集)上训练和测试了模型。我们得到的准确度为≈ 73% 这不是很好,但考虑到我们已经使用决策树桩进行分类(仅拆分数据集一次),这也不算太糟糕。
接下来,让我们看看如何使用增强决策树桩方法来改进这个结果。可能有点令人困惑的一件事是,在我们到达最终*增强决策树桩*的路上,我们使用整个数据集作为训练和测试数据集(我们不进行训练测试拆分)。您可能还记得,我们通常想要一个训练集,我们在其上训练模型和一个测试集,我们在其上测试模型 - 然而,对于 Boosting,我们例外并使用整个数据集进行训练和测试 - 只要保持这个例外记-。
类 提升:
def __init__ ( self , dataset , T , test_dataset ):
self 。数据集 = 数据集
自我。T = T
自我。test_dataset = test_dataset
self 。alphas = None
self 。模型 = 无
self 。准确性 = []
自我。预测 = 无
def fit ( self ):
# 设置描述性特征和目标特征
X = self . 数据集。drop ([ 'target' ], axis = 1 )
Y = self 。数据集[ '目标' ] 。where ( self . dataset [ 'target' ] == 1 , - 1 )
# 用 wi = 1/N 初始化每个样本的权重并创建一个数据框,在其中计算
评估 Evaluation = pd 。数据帧(ý 。复制())
评价[ '权重' ] = 1 / LEN (自我。数据集) #设置初始权重w = 1 / N
# 通过创建 T 个“加权模型”运行 boosting 算法
阿尔法 = []
模型 = []
用于 吨 在 范围(自。Ť ):
# 训练决策树桩
Tree_model = DecisionTreeClassifier ( criteria = "entropy" , max_depth = 1 ) # 注意决策树桩 --> 决策树桩
# 我们知道我们必须在加权数据集上训练我们的决策树桩,其中权重取决于
# 先前决策树桩
的结果。为了实现这一点,我们使用上面创建的#'evaluation dataframe'
的 'weights' 列以及fit 方法的 sample_weight 参数。# sample_weights 参数的文档说:“[...] 如果没有,那么样本的权重相等。”
# 因此,如果 NOT None,则样本的权重不同,因此我们创建了一个 WEIGHTED 数据集
# 这正是我们想要的。
模型 = Tree_model 。拟合( X , Y , sample_weight = np. 数组(评估[ '权重' ]))
#将单个弱分类器附加到一个列表中,该列表稍后用于制作
#加权决策
模型。追加(模型)
预测 = 模型。预测( X )
分数 = 模型。得分( X , Y )
# 将值添加到评估数据帧
评估[ 'predictions' ] = 预测
评估[ 'evaluation' ] = np . 其中( Evaluation [ 'predictions' ] == Evaluation [ 'target' ], 1 , 0 )
Evaluation [ 'misclassified' ] = np 。其中(评估[ '预测' ] != 评估[ '目标' ],1 , 0 )
# 计算误分类率和准确率
accuracy = sum ( Evaluation [ 'evaluation' ]) / len ( Evaluation [ 'evaluation' ])
misclassification = sum ( Evaluation [ 'misclassified' ]) / len ( Evaluation [ 'misclassified' ])
# 计算错误
err = np . sum ( Evaluation [ 'weights' ] * Evaluation [ 'misclassified' ]) / np 。sum (评估[ '权重' ])
# 计算 alpha 值
alpha = np . 记录(( 1 - err ) / err )
alphas 。追加(阿尔法)
# 更新权重 wi --> 这些更新后的权重用于 sample_weight 参数
# 用于训练下一个决策树桩。
评估[ '权重' ] *= np 。exp ( alpha * Evaluation [ 'misclassified' ])
#print('{0}.模型的准确度为:'.format(t+1),accuracy*100,'%')
#print('误分类率为:',misclassification*100,'%' )
自我。阿尔法 = 阿尔法
自我。模型 = 模型
def 预测( self ):
X_test = self 。测试数据集。drop ([ 'target' ], axis = 1 ) 。reindex ( range ( len ( self . test_dataset )))
Y_test = self 。test_dataset [ '目标' ] 。reindex ( range ( len ( self . test_dataset ))) 。其中(自我。数据集[ '目标' ] == 1 , - 1 )
# 对 self.model 列表中的每个模型进行预测
准确率 = []
预测 = []
为 阿尔法,模型 在 拉链(自我。阿尔法,自我。模型):
预测 = 阿尔法*模型。predict ( X_test ) #我们对列表
预测中的单个决策树分类器模型使用predict方法。追加(预测)
自我。准确性。追加( np . sum ( np . sign ( np .总和(NP 。阵列(预测),轴线= 0 ))== Y_test 。values ) / len ( predictions [ 0 ]))
# 上面的代码行可能有点混乱,因此我将完成单个步骤:
# 目标:创建一个准确度列表,可用于绘制准确度用于模型的基础学习器的数量
# 1. np.array(predictions) --> 这是包含单个模型预测的数组。它的形状为 8124xn
# 因此看起来像 [[0.998,0.87,...0.87...],[...],[...],[0.99,1.23,...,1.05,0,99...] ]
# 2. np.sum(np.array(predictions),axis=0) --> 总结列表的第一个元素,即 0,998+...+...+0.99。这是
#做是因为对于预测公式要我们总结了所有模型的预测数据集中每个实例。
# 因此,如果我们有例如 3 个模型,则预测数组的形状为 8124x3(想象一个有 3 列和
#8124 行
的表格)。这里第一列包含第一个模型的预测,第二列包含第二个模型的预测,第三列包含第三个模型的预测(注意
#第二个和第三个模型受第一个结果的影响,尤其是第一个和
#第二个模型)。这是合乎逻辑的,因为列(模型)
#n-1 的结果用于更改第 n 个模型的权重,然后使用第 n 个模型的结果来更改
n+1 模型
的权重。# 3. np.sign(np.sum(np.array(predictions),axis=0)) --> 由于我们的测试目标数据是 {-1,1} 的元素,我们希望
# 在同样的格式,我们使用sign函数。因此,accuracy 数组中的每一列就像
# [-0.998,1.002,1.24,...,-0.89] 并且每个元素代表该列上所有模型的组合和加权预测
#(例如,如果我们在第 5 列中,对于第 4 个实例,我们会找到值 -0.989,该值表示
具有 5 个基学习器的增强模型
的# 加权预测,用于第 4 个实例。第 6 个实例的第 4 个实例列代表# 具有 6 个基学习器的增强模型的加权和组合预测,而第 4 列的第 4 个实例代表
# 具有 4 个基学习器的模型的预测等等......)。长话短说,我们
对这些未来预测的符号
很感兴趣。如果符号是正的,我们知道真正的预测更有可能是正 (1) 然后# 负 (-1)。值越高(正值或负值),模型返回正确预测的可能性就越大。
# 4. np.sum(np.sign(np.sum(np.array(predictions),axis=0))==Y_test.values)/len(predictions[0]) --> 最后一步我们有将数组
# 转换为形状 8124x1,其中实例是元素 {-1,1},因此我们现在可以将这个
预测与我们的目标特征值
进行比较。目标特征数组的形状为 8124x1,因为对于每一行,它只包含一个预测 {-1,1},就像我们刚刚在上面创建的数组一样 --> 准备比较;)。
# 比较是通过 == Y_test.values 命令完成的。结果我们得到一个
形状为 8124x1的# 数组,其中实例是 {True,False} 的元素(如果我们的预测与
# 目标特征值,否则为 False)。由于我们要计算百分比值,因此必须计算
已正确分类
的# 个实例的比例。因此,我们简单地将上面的比较数组# 与沿轴 0 的元素 {True,False}
相加。# 并将其除以总行数 (8124),因为 True 与 1 相同,而 False 与 0 相同. 因此,正确的预测会
增加总和,而错误的预测不会改变总和。如果我们没有预测正确,则计算结果为 0/8124 并且
#
随之为0,如果我们预测一切正确,则计算结果为 8124/8124 并因此为 1。# 5. self.accuracy.append(np.sum(np.sign(np) .sum(np.array(predictions),axis=0))==Y_test.values)/len(predictions[0])) -->
# 计算完以上步骤后,我们将结果添加到 self.accuracy 列表中。这个列表的形状为 nx 1,也就是说,
#对于一个有 5 个基学习器的模型,这个列表有 5 个条目,其中第 5 个条目表示当所有
#5 个基学习器组合
时模型的准确性,第 4 个元素表示模型的准确性当 4 个基学习器组合时的模型等等。这个# 过程已经在上面解释过了。就是这样,我们可以绘制准确性。
自我。预测 = np 。符号(np . sum (np . array (预测),轴= 0))
######根据使用的树桩模型数量绘制模型的准确性##########
number_of_base_learners = 50
无花果 = plt 。图( figsize = ( 10 , 10 ))
ax0 = fig . add_subplot ( 111 )
对于 我 在 范围(number_of_base_learners ):
模型 = 助推(数据集,我,数据集)
模型。拟合()
模型。预测()
轴0 。绘图(范围(len (模型。准确度)),模型。准确度,'-b' )
ax0 。set_xlabel ( '#用于提升的模型' )
ax0 。set_ylabel (“精度” )
打印(“具有一批” ,number_of_base_learners ,“基本模型我们收到的精度” ,模型。准确性[ - 1 ] * 100, '%' )
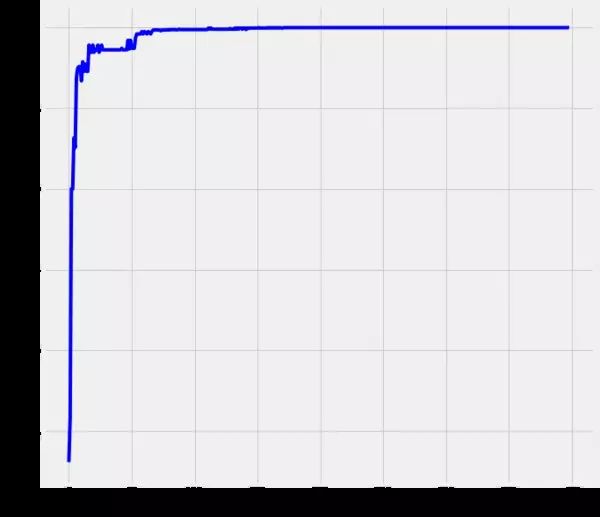
PLT 。显示()
输出:
正如我们所见,这些增强的决策树桩的预测能力确实令人惊叹。对于 8000 多个测试实例,我们都得到了正确的结果,因此使用包含 400 个基本学习器的模型的准确度为 100%。同样有趣的是,准确度迅速增加到≈ 10 个基础学习者和 ≈70 个基本学习器,我们的模型返回接近 100% 的准确率。
尽管如此,请允许我做一个侧节点。首先,这种提升模型的计算成本有点高,也就是说,它的预测能力伴随着计算成本的代价,因此我们必须在准确性和计算工作量之间做出折衷。以上面的例子我们需要≈ 400 个基础学习器获得 100% 的准确率,但 ≈70 个决策树桩我们已经接近 100%。因此,我们必须决定 100% 标记的重要性。其次,上面显示的模型根本没有声称计算效率高。该模型应该展示如何在不考虑计算效率的情况下从头开始创建增强决策树桩。因此,肯定有方法可以使上述代码更高效,从而使模型更快。这取决于您,玩弄代码并检查您是否可以,例如,实现一些矢量化计算而不是循环或类似的东西。python学习资源汇总 腾讯文档
使用 sklearn 提升
与往常一样,我们现在将使用预先打包的 sklearn AdaBoostClassifier,并将参数设置为我们上面使用的相同值。文档说:
“An AdaBoost [Y. Freund, R. Schapire, “A Decision-Theoretic Generalization of Online Learning and an Application to Boosting”, 1995] 分类器是一个元估计器,它首先在原始数据集,然后在同一数据集上拟合分类器的其他副本,但会调整错误分类实例的权重,以便后续分类器更多地关注困难案例。” [1]
我们要调整的参数是:
- base_estimator:我们将其设置为默认值,即上面使用的DecisionTreeClassifier。请注意,我们还可以定义一个像 estimator= DecisionTreeClassifier这样的变量,并通过设置 max_depth = 1、criterion = "entropy" 来参数化这个估计器,...但为了方便起见,我们将在这里省略它
- n_estimators:这是应该使用的基本学习器的数量。我们如上所述将其设置为 400。
- learning_rate:默认值是 1.0 并通过学习率减少每棵树的贡献。我们将其设置为默认值,因为我们没有明确合并学习率。
其余参数设置为默认值。
from sklearn.ensemble import AdaBoostClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.tree import DecisionTreeClassifier
for label in dataset 。列:
数据集[标签] = LabelEncoder () 。适合(数据集[标签])。变换(数据集[标签])
X = 数据集。drop ([ 'target' ], axis = 1 )
Y = dataset [ 'target' ]
#model = DecisionTreeClassifier(criterion='entropy',max_depth=1)
#AdaBoost = AdaBoostClassifier(base_estimator= model,n_estimators=400,learning_rate=1)
AdaBoost = AdaBoostClassifier ( n_estimators = 400 , learning_rate = 1 , algorithm = 'SAMME' )
AdaBoost 。拟合( X , Y )
预测 = AdaBoost 。得分( X , Y )
打印('准确度为:' ,预测* 100 ,'%' )
输出:
准确度为:100.0%
完毕!
参考
- Hastie T.、Tibshirani R.、Jerome F.,2008年。统计学习的要素。第二版。加利福尼亚州斯坦福:施普林格
- James G.、Witten D.、Hastie T.、Tibshirani R.,2013 年。统计学习简介。加利福尼亚州洛杉矶、华盛顿州西雅图、加利福尼亚州斯坦福:斯普林格
- Kuhn M.、Johnson K.,2013 年。应用预测建模。格罗顿,康涅狄格州,密歇根州盐碱地:施普林格
- Schapire R.,1999 年。Boosing 简介。第十六届国际人工智能联合会议论文集。
- Freund Y., Schapire R., 1999. Boosing 的简短介绍。日本人工智能学会学报, 14(5), 771-780
- Schapire R.,约阿夫·F.,2012年推进。剑桥,马萨诸塞,伦敦,英国:麻省理工学院出版社
- Bishop C.,2006 年。模式识别和机器学习。英国剑桥:斯普林格
- Marsland S.,2015 年。机器学习算法视角。第二版。佛罗里达州博卡拉顿:CRC Press