数据结构---图

一.图的基本概念

在了解图之前我们先来想想生活中有哪些图？如果你是一名工科大学生的话你肯定会学过一门学科叫做工程制图：

在画图的时候一般都是先确定点的位置，比如说圆的圆心所在位置，两个圆相切的切点位置，正方形4个点的位置等等…点确定之后我们可以用线将其连接起来，两个点确定一条线，多条线就可以组成一个图，比如说下面的图片：

图看起来复杂但是他们本质上都是由点和线连接起来的。再比如说你是一个旅游爱好者的话那么你一定会经常会使用一个东西叫做地图，我们手机上就存在各种各样的地图，比如说百度地图，高德地图，谷歌地图等等，我们在地图里面输入起始点和目的地那么他就会自动显示一条路线出来，并且这条路线通常都是最好最合适的，那么这时我们就可以把目的地和起始点看成两个点，地图软件给我们提供的路线就可以看成连接两个点的直线，而目的地和其实点可以是任何位置，比如说武汉可以作为目的地，北京可以看成目的地，xxx酒店可以看成目的地等等等，那么将每个有特殊意义的位置都看成一个点的话，我们平时使用的地图也就可以看成是点的合集，而之所以将这些点称为地图就是因为这些点由各种线链接起来，那么我们就可以认为地图是由点和线连接起来，比如说下面的图片：

那么大致理解了生活中图的概念，那么我们就可以来了解了解数据结构中的图。

1.图的组成

英文单词group是图的意思，所以大家经常能够在网上看到有人这么表示图：G = (V， E)其中G表示图的意思，v的全称是vertex也就是顶点的意思，E的全称是edge也就是边的意思也可以认为是顶点和顶点的关系，那么这就说明数据结构中的图也是由点和边组成，比如说下面的图片：

这就是一个图这个图由4个顶点4条边组成，1号边将顶点A和B连接起来，2号边将顶点B和D连接起来，3号边将顶点D和C连接起来，4号边将顶点C和A连接起来，但是这里存在一个问题树好像也是由节点和边组成的啊，那能把树也看成是图吗？比如说下面的图片：

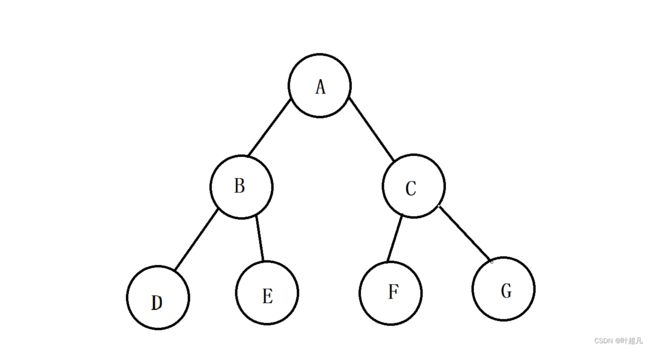
那么这里大家就要注意了，树是一种特殊（无环连通）的图但是图不一定是树，我们在使用树的时候关注点往往是节点中的值，而我们使用图的时候关注点往往是节点的值以及边的权值，所以可以认为树就是图但图不一定是树，那这里权值是什么意思呢？我们说边的作用是表示节点和节点之间的相连关系，那么它还有另外的一个功能就是记录特殊意义的数据，我们把这个数据称为权值，比如说下面的图片

这里边不仅可以表示节点和节点之间的关系还可以存储值用来表示某种意义，上图中权值可以表示两点之间火车票的价钱，比如说武汉到广东的火车票就是70元，武汉到合肥的火车票就是80元，武汉到北京的火车票这里两个节点没有连接所以就没有火车票卖，当然这里的权值还可以表示为两点之间的距离，那么根据图中的值就可以知道武汉到广东的距离就是70公里，武汉到合肥的距离就是80km，武汉到上海的距离暂且还不详因为两点没有连接起来我们不知道权值是多少，反正这里的权值可以表示一些信息，具体什么信息又我们自己决定。那么看到这里想必大家就应该能够明白图的组成：顶点(有哪些元素) 边(哪些元素之间有关系) 权值(关系表示什么？具体大小为多少？),
那么我们接着来看有向图和无向图分别表示什么。

2.有向图和无向图

在做的各位肯定都用QQ和微信这两个聊天软件，当我们成功添加一个人为好友时他会成为我的好友，而我也会成为他的好友，这是一个相互的关系，但是当我们使用抖音或者快手关注某个人的时候他会成为我的关注对象，但是我会成为他的关注对象吗？不一定对吧，那么QQ和微信中的好友列表就相当于无向图一旦两个节点存在联系，那么这个联系就一定是相互的，而抖音和快手中的关注就相当于有向图，A跟B有关系但是B不一定跟A存在关系，具体反应到图像上就是这样，无向图就是这样：

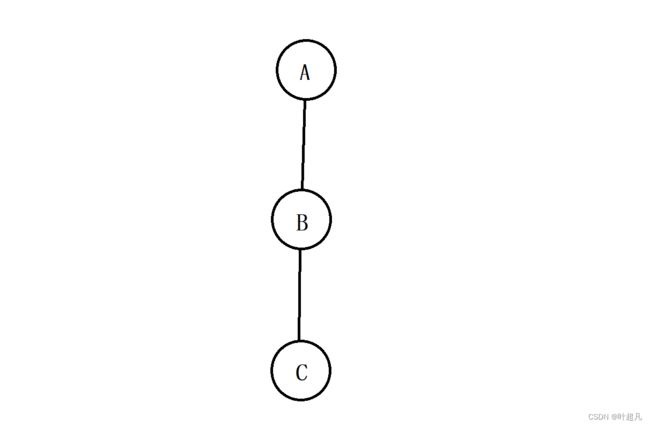
有向图就是这样：

A跟B有关系，B跟A有关系，B跟C有关系但是C不一定和B有关系，那么这就是有向图和无向图之间的区别，当顶点之间存在很强的关系时就用无向图比如说qq微信好友，城市之间的距离等等等，当节点之间的关系没有那么强时就用有向图比如说抖音上的朋友(你关注了我并且我也关注了你才能成为朋友)，人际关系(我认识某个人但是那个人不认识我)等等等。

3.完全图

在有n个顶点的无向图中，若有n * (n-1)/2条边，即任意两个顶点之间有且仅有一条边，则称此图为无向完全图，比如说下面的图片：

在n个顶点的有向图中，若有n * (n-1)条边，即任意两个顶点之间有且仅有方向相反的边，则称此图为有向完全图，比如说下面的图片：

这个概念还是挺重要的希望大家能够记住。

4.邻接顶点

在无向图中G中，若(u, v)是E(G)中的一条边，则称u和v互为邻接顶点，并称边(u,v)依附于顶点u和v；在有向图G中，若是E(G)中的一条边，则称顶点u邻接到v，顶点v邻接自顶点u，并称边与顶点u和顶点v相关联。
这个概念不重要大家可以跳过。

5.顶点的度

顶点v的度是指与它相关联的边的条数，记作deg(v)。在有向图中，顶点的度等于该顶点的入度与出度之和，其中顶点v的入度是以v为终点的有向边的条数，记作indev(v);顶点v的出度是以v为起始点的有向边的条数，记作outdev(v)。因此：dev(v) = indev(v) + outdev(v)。比如说下面的图片：

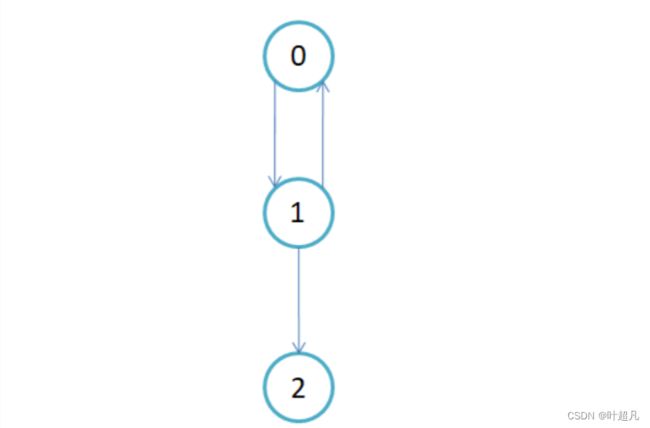
顶点0有一条指向外面的线所以他的出度为1，有一条指向内部的线所以他的入度为1，所以节点1的度为2。那么这里大家要注意的一点就是：对于无向图，顶点的度等于该顶点的入度和出度，即dev(v) = indev(v) = outdev(v)。

6.路径和路径长度

在图G = (V， E)中，若从顶点vi出发有一组边使其可到达顶点vj，则称顶点vi到顶点vj的顶点序列为从顶点vi到顶点vj的路径。比如说下面的图片

从节点D到节点B有多个路径可以走比如说：D -> C -> B或者D -> B 或者 D -> C -> B再或者D -> C -> A ->B，这里就简单的列出来了4条路径，因为上述图可以循环所以按道理可以列出来更多的路径这里就不一 一列举，那么这就是路径的概念，而路径长度就是将路径中所有边的权值全部相加比如说路径D C A B的路径长度就是40+30+20=90,对于不带权的图，一条路径的路径长度是指该路径上的边的条数，那么这就是路径长度的定义。

7.简单路径和回路

若路径上各顶点v1，v2，v3，…，vm均不重复，则称这样的路径为简单路径。若路径上第一个顶点v1和最后一个顶点vm重合，则称这样的路径为回路或环。比如说下面的图片：

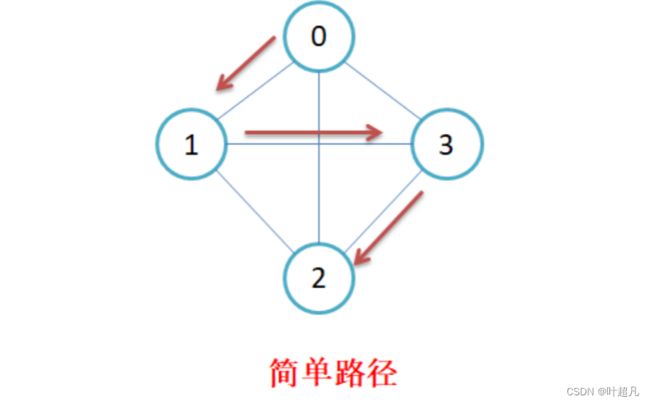
路径0 1 3 2 中没有重复节点那么这就是一个简单路径

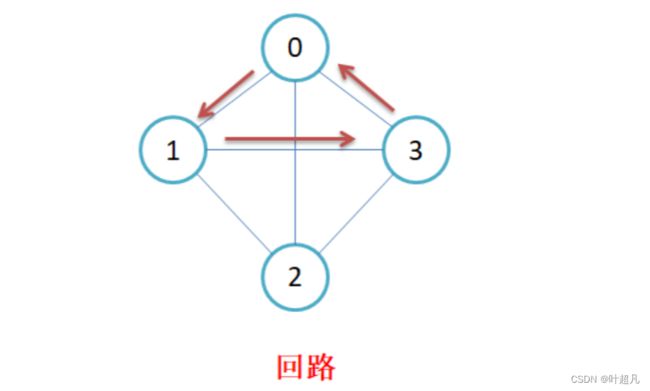
这里的路径为0 1 3 0存在重复的节点所以他不为简单路径而是回路或者是环。

8.子图

设图G = {V, E}和图G1 = {V1，E1}，若V1属于V且E1属于E，则称G1是G的子图。简单的说就是如果A图中的节点和边在B图中都存在那么我们就称A为B的子图。比如说下面的图片：

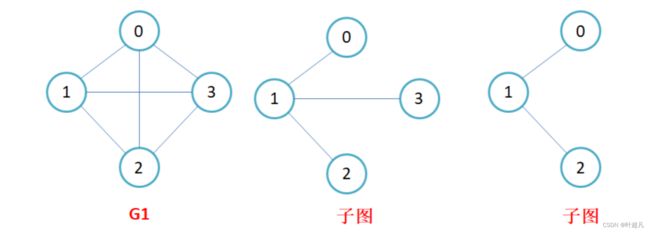
9.连接图和强连接图

在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的，则称此图为连通图。在有向图中，若在每一对顶点vi和vj之间都存在一条从vi到vj的路径，也存在一条从vj到vi的路径，则称此图是强连通图。

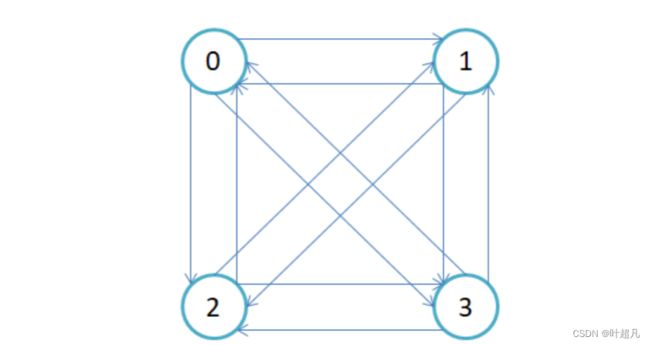
这个图就是一个强连接图，因为每个节点都可以相互抵达。

这个图就是一个连接图因为任意节点之间都存在路径。

10.生成树

一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n1条边，比如说一个连接图为这样：

那么他的生成树就应该是这样：

用最少的线将每个节点都连接起来就是生成树。

二.图的存储结构

图是一个很复杂的结构，他既不像二叉树一样那么有规律每个节点都有一个左节点和右节点，也不像vector一样那么简单申请一段连续的空间就可以，图的结构千变万化既可以变成树一样也可以变成链表一样，所以要想存储图的数据我们只能将其全部打散，我们说图是由顶点，边，权值组成，那么这里就可以使用多个容器来分别进行存储，比如说创建一个vector对象来专门存储节点的值，再创建一个map来存储节点和它对应的数组下标，这样就可以更加方便的找到元素，最后再创建一个容器用来存储边和权值，那么这里就存在一个问题该选择什么样的容器呢？那么这里就给出了两种解决方案。

1.邻接矩阵的原理

邻接矩阵是通过创建二维数组的方法来存储图的边，当一个图存有5个节点时我们可以开辟一个55的二维数组，数组中的下标就表示节点之间连接的情况，比如说下标为1 2元素就表示第2号顶点和第3号顶点的连接情况，如果没有连接的化我们就可以使用无穷大来表示两节点没有连接，如果连接了并且权值为10的化我们就把下标为1 2的元素赋值为10，比如说下面的图片：

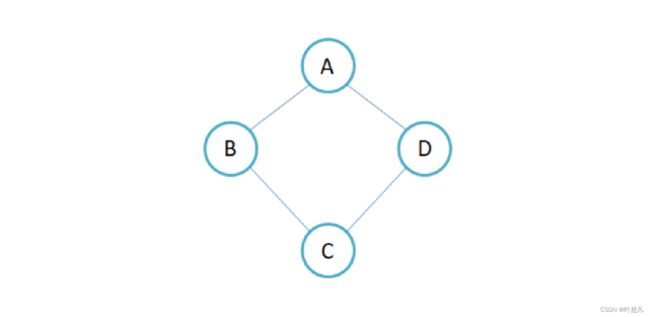
当前图存在4个节点，所以我们就可以创建一个44的二维数组，因为当前图不存在权值所以我们就用1来表示两个节点连接，A B C D对应的下标为 0 1 2 3，因为节点本身肯定是相互连接的，所以一开始我们就可以将下标为 (0,0) (1,1) (2,2) (3,3)的值初始化为1，因为这里是无向图一旦连接就是相互连接，所以当顶点A和B连接时我们就要将下标(0,1) (1,0)的元素初始化为1，B和C连接时就要将下标(1,2)和(2,1)的元素赋值为1，如果两个节点没有连接我们就用无穷大来表示，那么依次类推就可以得到下面的图片:

通过观察不难发现这里的二维数组是关于斜直线对称的，在使用的过程中用一半就行，如果是有向图的话这里就不能使用一半，比如说下面的图片：

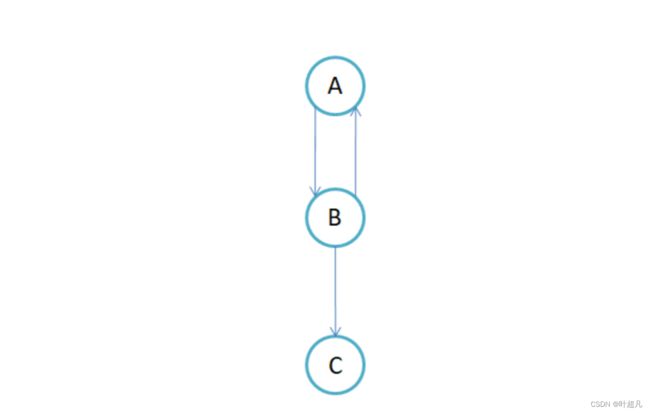
这里存在三个节点所以我们得创建一个3*3的二维数组元素A B C分别对应下标0 1 2 ，B单向连接了C所以我们就只能将下标为 (1 ,2)的元素赋值为1切记这里不能把下标(2,1)的元素也初始化为1，因为这里是单项连接所以二维数组就变成了下面这样：

那么这就是邻接矩阵的原理。

2.邻接矩阵的模拟实现

首先这个类肯定得是一个模板类，并且模板中得有个参数表示顶点的类型，有个参数表示权值的类型，有个参数表示两个顶点不相连，如果我们擅自使用0或者其他值来表示两个顶点不相连，当出现一条边的权值确实为0或者那个值的话就会出现问题，最后还需要一个参数表示当前的矩阵为单项还是双向，然后在类的里面我们就创建三个成员变量一个为一维数组用来存储顶点的值，一个map用来存储值和下标的对应关系这样方便我们找边的对应关系，最后就是二维数据用来存储边的关系，那么这里的代码如下：

template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
class Graph
{
public:

private:
	map<V, size_t> _vIndexMap;	 // 顶点和下标的对应关系
	vector<V> _vertexs;			 // 顶点集合
	vector<vector<W>> _matrix;   // 存储边集合的矩阵
};

构造函数有两个参数一个是V类型的指针表示传递一个V类型的数组用来构造，另外一个是无符号整型表示当前图有多少个元素，那么在函数的开始我们就使用for循环往数组_vertexs里面插入数据，因为一开始数组为空循环的次数和下标刚好对应，所以我们也可以顺便往_vIndexMap里面插入数据，map中的V表示顶点的值size_t表示下标的值，最后再用for循环对_matrix数组的每个元素都进行增长并将里面的值都赋值为INT_MAX，那么这里的代码如下：

Graph(const V* vertexs, size_t nums)
{
	for (int i = 0; i < nums; i++)
	{
		_vertexs.push_back(vertexs[i]);
		_vIndexMap[vertexs[i]] = i;
	}
	_matrix.resize(nums);
	for (int i = 0; i < nums; i++)
	{
		_matrix[i].resize(nums, MAX_W);
	}
}

构造函数的功能是往容器里面添加顶点，那么我们还需要一个函数往图里面添加边，这个函数有三个参数其中两个表示边的起点元素和终点元素最后一个表示边的权值：

void AddEdge(const V& src, const V& dst, const W& w)
{

}

函数的第一步就是找到这两个元素对应的下标，因为查找元素下标的功能后面会经常使用，所以我们就可以写一个查找函数专门用来获取元素的下标，那么这里大家要注意一点就是查找的时候不能使用[ ]，因为一旦用户输入一个不存在的值时，它会直接将该元素插入到容器里面这样就不符合我们的预期，所以在查找的时候得使用变量来记录find函数的返回值，如果变量的值不等于end的话就表明元素存在，返回变量的second就行，如果等于end的话就表明元素不存在我们就直接抛出异常并返回-1

size_t GetVertexIndex(const V& v)
{
	auto it = _vIndexMap.find(v);
	if (it != _vIndexMap.end())
	{
		return it->second;
	}
	else
	{
		throw invalid_argument("顶点不存在");
		return -1;
	}
}

有了这个函数之后在AddEdge函数里面我们就可以先用GetVertexIndex函数找到起始元素和终点元素的下标：

void AddEdge(const V& src, const V& dst, const W& w)
{
	size_t x1 = GetVertexIndex(src);
	size_t x2 = GetVertexIndex(dst);
}

然后将二维数组中下标为(x1,x2)的元素赋值为 w，如果Direction的值为false的话就表示当前的图为无向图我们还得将下标为(x2,x1)的元素也赋值为w，那么这里可以用if语句来实现：

void _AddEdge(size_t srci, size_t dsti, const W& w)
{
	_matrix[srci][dsti] = w;
	if (Direction == false)
	{
		//当前为无向图
		_matrix[dsti][srci] = w;
	}
}
void AddEdge(const V& src, const V& dst, const W& w)
{
	size_t x1 = GetVertexIndex(src);
	size_t x2 = GetVertexIndex(dst);
	_AddEdge(x1, x2, w);
}

构造函数用来存储顶点，AddEdge函数用来存储边，那么到这里我们的邻接矩阵的存储形式就完成了，接下来我们来进行测试。

3.邻接矩阵的测试

为了方便后面的测试我们这里先创建一个print函数，在这个函数里面我们要打印出每个顶点相连的其他顶点，然后再将存储边的二维数组打印出来，那么这个函数就很简单，打印相连的顶点直接遍历二维数组的每一行或者列即可，打印边的连接情况时直接用嵌套的for循环遍历即可，那么这里的代码如下：

void print()
{
	for (int i = 0; i < _matrix.size(); i++)
	{
		cout << "[" << _vertexs[i] <<"]";
		for (int j = 0; j < _matrix.size(); j++)
		{
			if ( _matrix[i][j]!=MAX_W)
			{
				cout << "->" << _vertexs[j];
			}
		}
		cout << endl;
	}
	cout<<endl;
	for (int i = 0; i < _matrix.size(); i++)
	{
		for (int j = 0; j < _matrix.size(); j++)
		{
			if (_matrix[i][j] != MAX_W)
			{
				cout << _matrix[i][j] << " ";
			}
			else
			{
				cout << "*" << " ";//这里用*表示没有连接
			}
		}
		cout << endl;
	}
}

然后我们就可以用下面的代码来进行测试：

int main()
{
	const char* tmp = "0123";
	Graph<char, int, INT_MAX, true> g(tmp, 4);
	g.AddEdge('0', '1', 1);
	g.AddEdge('0', '3', 4);
	g.AddEdge('1', '3', 2);
	g.AddEdge('1', '2', 9);
	g.AddEdge('2', '3', 8);
	g.AddEdge('2', '1', 5);
	g.AddEdge('2', '0', 3);
	g.AddEdge('3', '2', 6);
	g.print();
	return 0;
}

代码的运行结果如下：

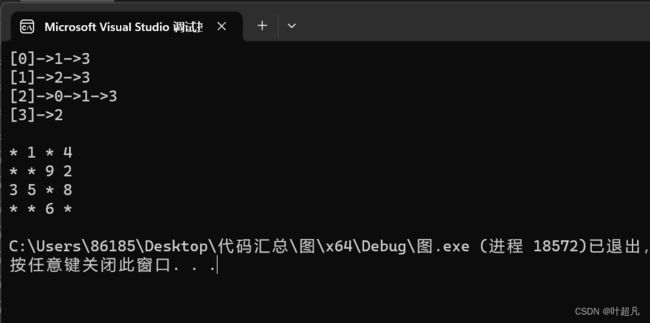
这个测试的实际图片是下面这样：

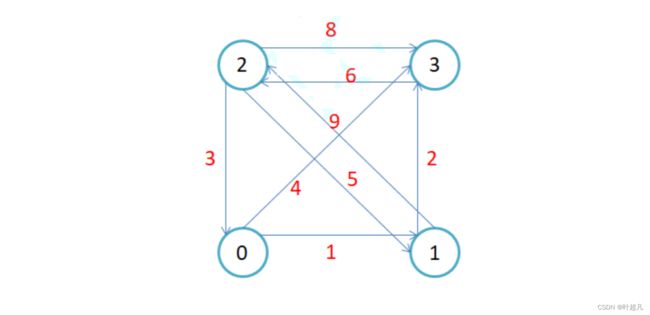
那么大家仔细地比对一下便可以看到这里地运行结果是没有问题地。

4.邻接表的原理

邻接表是通过创建一个指针数组的方式来记录每个顶点的连接情况，如果一个图中含有4个顶点那么这个指针数组里面就会有对应的4个元素，每个元素都记录着当前节点的存储情况，比如说下面的图片：

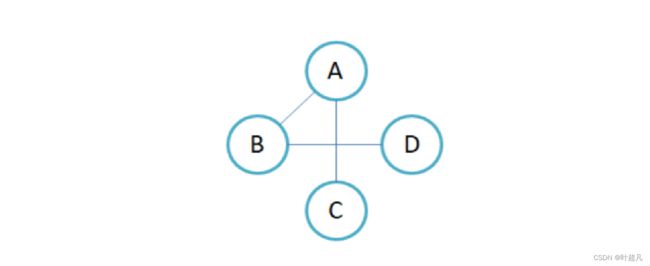
当前图存在4个顶点，所以我们就创建一个含有4个元素的指针数组，每个指针都指向与此相连的顶点，这些顶点再彼此相连成为一个链表，那么上面的图片用邻接表表示就应该是下面这样：

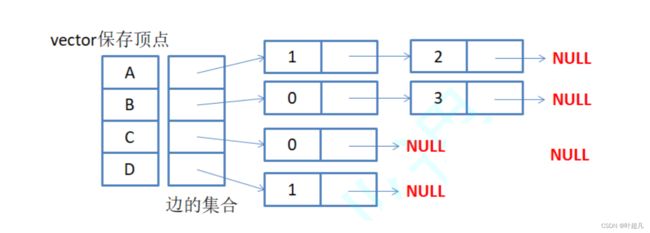
指针数组的下标与元素相对应，下标0 1 2 3分别表示元素A B C D，因为A连接了顶点B C所以下标为0的指针连接的链表有两个节点，这两个节点存储了被连接元素所对应的下标也就是1和2，同理元素D连接了元素B所以下标为3的指针连接的链表只有一个节点，这个节点存储的是B的下标也就是1，那么这就是邻接表的原理通过创建指针数组和链表的方式来记录顶点的连接情况，那么上面的逻辑适用于无向图，对于有向图这里得做一个区分，有向图的邻接表分为入边表和出边表，入边表就是记录所有指向该节点的边不记录该节点指向其他节点的边，而出边表则是记录该节点指向其他节点的边，不记录其他顶点指向该节点的边，比如说图长下面这样：

那么它的入边表就是下面这样：

因为只有E顶点指向A顶点所以下标为0的指针指向的链表只有一个元素并且该元素的下表为4，因为元素A和元素C都指向元素D，所以下标为3的指针指向的链表就有两个元素，并且这两个元素的下标为0和2，同理出边表的原理也相同，这里就不多说了，大家直接看图：

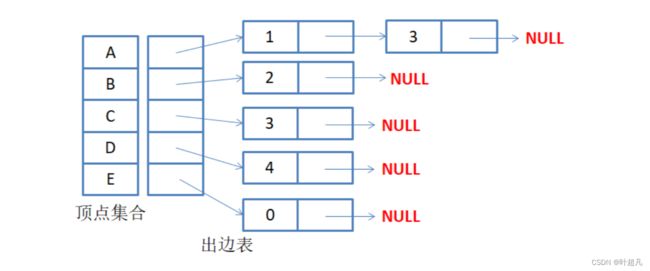
那么接下来我们就模拟实现以下邻接表的存储形式。

5.邻接表的模拟实现

首先需要一个数组来存储顶点，并且为了方便找到元素和下标的关系还得创建一个map对象来进行存储，最后再创建一个指针数组用于存储边的关系，因为指针指向的节点里面不仅得存储元素对应的下标以及这个边的权值，还得存储下一个节点的位置，所以还得创建一个类用来描述节点，那么这里的代码如下：

template<class W>
struct LinkEdge
{
	LinkEdge(const W& w)
		:_w(w)
		,_destindex(-1)
		,_next(nullptr)
	{}
	W _w;
	int _destindex;
	LinkEdge* _next;
};
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
class graph
{
public:
	typedef LinkEdge<W> Edge;
private:
	vector<V>  _vertexs;//顶点的集合
	map<V, int> _vIndexMap;//顶点和下标的对应关系
	vector<Edge*> _linkTable;//边的关系
};

构造函数需要两个参数一个是顶点的数组，另外一个就是顶点的个数，那么这里就跟邻接矩阵是相同的道理，尾插元素进数组的同时，将元素和下标对应的关系顺便插入到map容器里面，然后将指针数组的长度扩展为顶点的个数，那么这里的代码就如下：

graph(const V* vertexs, size_t n)
{
	for (int i = 0; i < n; i++)
	{
		_vertexs.push_back(vertexs[i]);
		_vIndexMap[vertexs[i]] = i;
	}
	_linkTable.resize(n);
}

构造函数完成之后就要实现添加边的函数，这个函数需要三个参数其中两个表示边的起点和终点另外一个参数表示边的权值，在函数的开始就要找到这两个元素所对应的下标，因为这里查找下标的原理跟邻接矩阵相同所以这里可以把GetVertexIndex函数原封不动的搬过来，那么这里的代码就如下：

size_t GetVertexIndex(const V& v)
{
	auto it = _vIndexMap.find(v);
	if (it != _vIndexMap.end())
	{
		return it->second;
	}
	else
	{
		throw invalid_argument("顶点不存在");
		return -1;
	}
}
void AddEdge(const V& src, const V& dst, const W& w)
{
	size_t _src = GetVertexIndex(src);
	size_t _dst = GetVertexIndex(dst);
}

然后我们就可以根据_src的值找到指针数组对应的元素，并创建出一个边的节点将节点内部的_destindex值初始化为_dst,然后将该节点的头插到对应位置，那么这里的代码如下：

void AddEdge(const V& src, const V& dst, const W& w)
{
	size_t _src = GetVertexIndex(src);
	size_t _dst = GetVertexIndex(dst);
	Edge* new_edge = new Edge(w);
	new_edge->_destindex = _dst;
	new_edge->_next = _linkTable[_src];
	_linkTable[_src] = new_edge;
}

如果当前为无向图的话我们还得在_dst位置上再添加头插一个节点，该节点记录的权值为w下标为src，那么这里可以通过if语句来实现：

void AddEdge(const V& src, const V& dst, const W& w)
{
	size_t _src = GetVertexIndex(src);
	size_t _dst = GetVertexIndex(dst);
	Edge* new_edge = new Edge(w);
	new_edge->_destindex = _dst;
	new_edge->_next = _linkTable[_src];
	_linkTable[_src] = new_edge;
	if (Direction == false)
	{
		Edge* new_edges = new Edge(w);
		new_edges->_destindex = _src;
		new_edges->_next = _linkTable[_dst];
		_linkTable[_dst] = new_edges;
	}
}

我们这里只实现了出边表因为入边表平时我们很少用，所以我们就只实现出变表，那么接下来我们就要对上面实现的代码进行测试。

6.邻接表的测试

首先得创建print函数，这个函数可以通过for循环加内嵌while遍历指针中的每个链表，打印边的同时将边的权值也顺便打印出来，那么这里的代码就如下：

void print()
{
	for (int i = 0; i < _linkTable.size(); i++)
	{
		Edge* tmp = _linkTable[i];
		cout <<"[" << _vertexs[i]<<"]";
		while (tmp != nullptr)
		{
			cout << "-" << tmp->_w << "->"<<_vertexs[tmp->_destindex];
			tmp = tmp->_next;
		}
		cout << endl;
	}
}

然后我们就可以使用下面的代码来进行测试：

void test2()
{
	string a[] = { "张三", "李四", "王五", "赵六" };
	graph<string, int, true> g1(a, 4);
	g1.AddEdge("张三", "李四", 100);
	g1.AddEdge("张三", "王五", 200);
	g1.AddEdge("王五", "赵六", 30);
	g1.print();
}

代码的运行结果如下：

大家自行对比可以看到这里代码的实现逻辑没有问题，那么这里就是邻接表的实现方法，这种方法后面不常用，我们后面简介的各种各种算法都是用邻接矩阵的方式来实现。

三.图的遍历

图的遍历有两种方法，一种是广度优先一种是深度优先，我们先来了解一下这两种遍历的区别：

这里有三个大正方形并且大正方形里面还有两个小正方形，正方形的颜色分别为蓝红绿，我们就把正方形看成一个盒子，所以这里就有3个蓝色大盒子，每个蓝色盒子里面装着一个中等的红色盒子，每个红色盒子里面又装着一个绿色的小盒子，那么这时有个玩具藏在某个盒子里面，我们要找到这个玩具就只能一个一个的把每个盒子都打开，那么这里打开的方式就大致分为两种，第一种就是：先分别打开外层的三个红色盒子进行查找，如果没有的话再分别打开内部的三个绿色中等盒子进行查找，如果还没有的话最后分别打开三个最小的绿色盒子进行查找。第二种就先一口气打开某个蓝色盒子中的所有盒子，如果没有的话再一口气打开另外一个蓝色盒子中的所有盒子，如果还没有的话就打开剩下蓝色盒子中的所有盒子，这就是第二种方法。我们把第一种方法称为广度优先它是把当前所有能走的步骤全部走完再走下一步，而第二种方法就是深度优先它是先一步完全走到头然后再走第二步，那么接下来我们就来实现一下图的广度优先和深度优先。

1.广度优先的原理

比如说我们的图长这个样子：

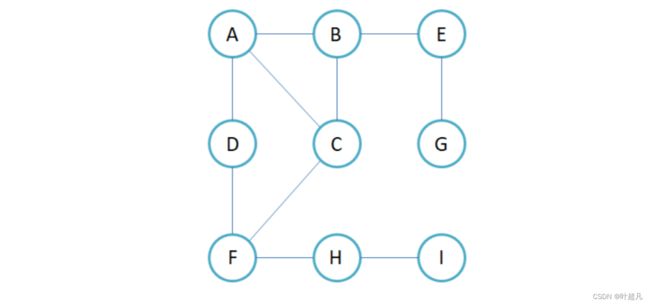
我们要从A节点开始以广度优先的方式遍历其他节点，那么第一轮遍历的节点就是与A节点直接相连的节点也就是B C D，然后再遍历与B C D直接相连的节点也就是F E A，因为A在之前的遍历过程中已经出现过这里得将其去掉，所以与B C D直接相连的点就是F和E,然后再遍历和F E相邻的节点，这样依次循环下去，那么遍历的结构就是这样：

这里实现的原理也很简单，因为用邻接矩阵采用二维数组的方式进行存储，所以我们可以创建一个队列一开始将A节点入队列然后再出队列，出的时候将与A节点相连的所有节点都入队列，因为可以通过GetVertexIndex函数得到出队列节点的下标，所以就可以在二维数组里面通过for循环找到与该节点相连的所有节点并依次将其入队列，当队列为空的时候就说明所有的节点都已经遍历完了，但是这里存在一个问题：将某个节点相连的节点都入队列，这里就可能存在重复的情况比如说A节点出队列的时候入了B节点，但是出B节点的时候AB也是相连的，这个时候又会把A入队列，所以这就可能导致死循环，那么为了解决这个问题我们就得再创建一个数组用来标记哪些节点我们已经被访问过了不需要再入队列，那么这就是广度优先的原理。

2.广度优先的模拟实现

首先这个函数需要一个参数用来表示遍历开始的节点，然后在函数里面创建一个数组用于标记哪些节点已经被访问，再创建一个队列来让元素按照顺序进行遍历：

	void BFS(const V& src)
	{
		vector<bool> flag(_vertexs.size());//标记元素是否已经遍历过
		queue<int> q1;//按照顺序依次遍历元素
	}

然后使用GetVertexIndex函数得到开始元素的下标，将该下标的元素入队列并将flag数组中对应的下标的值赋值为true，然后就创建一个while循环，循环内部先记录队列的头部元素然后将该元素删除，最后创建一个for循环将所有与该元素相连的点都入队列，入队列的同时将标记数组中对应元素的位置初始化为true，当队列为空时就表示遍历已经完成，那么这里的代码就如下：

void BFS(const V& src)
{
	vector<bool> flag(_vertexs.size());//标记元素是否已经遍历过
	queue<V> q1;//按照顺序依次遍历元素
	size_t srci = GetVertexIndex(src);//得到开始节点的下标
	q1.push(srci);
	flag[srci] = true;
	while (!q1.empty())
	{
		size_t _front = q1.front();//记录队列头部位置
		q1.pop();//将其删除
		cout << _vertexs[_front] << " ";//打印一下
		for (int i = 0; i < _matrix.size(); i++)
		{
			if (_matrix[_front][i] != MAX_W && flag[i] == false)
			{
				//如果该节点与其他节点相连并且那个节点之前没有遍历过
				q1.push(i);//将其入队列
				flag[i] = true;//做标记以及被访问过来以后不用入队列了
			}
		}
	}
}

我们可以用下面的代码来进行测试：

void test3()
{
	string a[] = { "张三", "李四", "王五", "赵六", "周七" };
	Graph<string, int> g1(a, sizeof(a) / sizeof(string));
	g1.AddEdge("张三", "李四", 100);
	g1.AddEdge("张三", "王五", 200);
	g1.AddEdge("王五", "赵六", 30);
	g1.AddEdge("王五", "周七", 30);
	g1.BFS("张三");
}

运行的结果如下：

我们可以画图来进行验证：

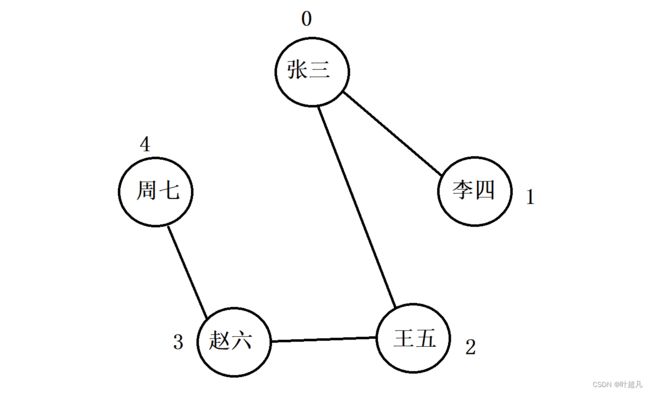
从张三（下标为0）开始遍历，与张三相连的时李四（下标为1）和王五（下标为2），因为李四的下标比王五小，所以李四先遍历王五后遍历，因为李四没有其他先俩姐对象所有就将赵六入队列，紧接着就是周七，所以广度遍历的顺序就是张三 李四 王五 赵六 周七，我们的运行结果符合预期那么就说明代码是正确的。

3.深度优先的原理

图的深度优先就是一条路走到黑，直到没有路可以走才往后走，比如说下面的图片：

当以A为起点的深度优先就是这样：

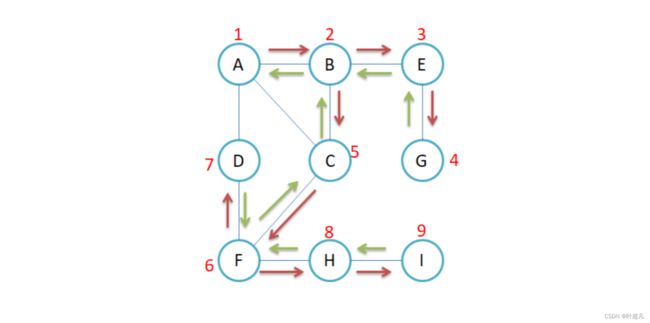
数字的下标表示遍历的顺序，所以这里的遍历顺序就是A到B，B到E，E到G，因为G没有路可以走了，所以就往回退来到了E，E这时只有一条路就是往G走可是G这条路已经走过了，所以E也没有路可以走了只能继续往回退来到B，B可以往E走也可以往C走，但是E已经走过了所以就只能往C走，C可以往A走也可以可以往F走因为A走过来所以只能往F走，F往H走,H往I走，I无路可走了就往回走来到了H，H无路可走了就往F走，F还可以往D走，所以就来到了D，D既不能往前走来到A也不能往后走来到F所以这里的遍历就结束了，那么这就是深度优先的遍历原理:一条路走到黑。

4.深度优先的模拟实现

首先使用者在实现这个函数进行遍历的时候只会传递一个参数表示顶点的开始，所以我们函数的参数只能有一个，但是深度优先得通过递归来实现，递归的过程中得不停的传递数组来判断哪些节点已经遍历过，所以得再添加一个函数来方便递归：

void _DFS(size_t srci, vector<bool>& visited)
{

}
void DFS(const V& src)
{

}

在DFS里面调用_DFS函数来实现递归，首先在DFS里面计算src对应的下标，然后创建一个标记数组，最后把这个数组和下标传递给_DFS，那么这里的代码如下：

void _DFS(size_t srci, vector<bool>& visited)
{

}
void DFS(const V& src)
{
	size_t srci = GetVertexIndex(src);
	vector<bool> visited(_matrix.size());
	visited[srci] = true;
	_DFS(srci, visited);
}

在_DFS里面先打印srci对应的数据，然后创建一个for循环，在循环里面遍历二维数组中的第srci-1行，如果存在相邻的节点没有遍历就递归便令该节点，那么这里的代码如下：

void _DFS(size_t srci, vector<bool>& visited)
{
	cout << _vertexs[srci] << " ";
	for (int i = 0; i < visited.size(); i++)
	{
		if (visited[i] == false && _matrix[srci][i] != MAX_W)
		{
			visited[i] = true;
			_DFS(i, visited);
		}
	}
}
void DFS(const V& src)
{
	size_t srci = GetVertexIndex(src);
	vector<bool> visited(_matrix.size());
	visited[srci] = true;
	_DFS(srci, visited);
}

可以用下面的代码来进行测试：

void test3()
{
	string a[] = { "张三", "李四", "王五", "赵六", "周七" };
	Graph<string, int> g1(a, sizeof(a) / sizeof(string));
	g1.AddEdge("张三", "李四", 100);
	g1.AddEdge("张三", "王五", 200);
	g1.AddEdge("王五", "赵六", 30);
	g1.AddEdge("王五", "周七", 30);
	g1.BFS("张三");
	cout << endl;
	g1.DFS("张三");
}

代码的运行结果如下：

可以看到这里遍历的结果和广度优先是一样的，对照之前的图也不难发现这里的结果确实是正确的：

四.最小生成树

在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的，则称此图为连通图，一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。那么最小生成树的概念就是权值相加最小的生成树，我们将其称为最小生成树，那么接下来我们就要讲解两个算法来求解一个图的最小生成树。

1.Kruskal算法原理

假设一个无向图存在n个节点，那么要想让所有节点全部连接起来则必须得有n-1条边少一条边都不行，如果边的个数大于n-1那么这些边组成的生成树就一定不是最小生成树，并且选出来的边组合在一起不能生成环，一旦生成环则必定会有个节点没有连接上，那么如何接下来我们就通过下面的图片来理解上面的话：这里有6个节点，添加第一条边上去可以将两个节点连接起来，这样待连接的节点数目就变成了4：

这时我们每添加一条边上去都可以将一个节点与已经被连接的节点连接起来，比如说下面的图片：

再添加一条边就是这样：

可以看到这里每添加一条边都可以消除一个待连接的节点，所以当有n个节点的时候要想让这些节点连接起来至少得有n-1条边，但是这里有个特例：添加边的两侧节点不能是已经被连接起来的节点因为添加这条边上去并不会减少待连接点的数量，比如说下面的图片：

所以在添加边的时候不能选择已经连接起来的节点，那么Kruskal的原理就是将整个图的边都放到一块，然后依次选出n-1条最小的边，这样这些边加起来的权值就是最小的，但是可能会出现一条边连接的节点都是已经被连接起来的，所以在选边的时候就得做出判断，那么这就是Kruskal算法的原理，我们来看看下面这张图片

边hg的权值为1它是最小的所以一开始我们就选着这条边，权值第二小的有两条边分别为ic和gf，因为这两条边连接起来都不会构成环，所以我们这里将两条边都选上：

接下来权值最小的边就是ab和cf，他们都选上也不会构成环，所以图片就变成下面这样：

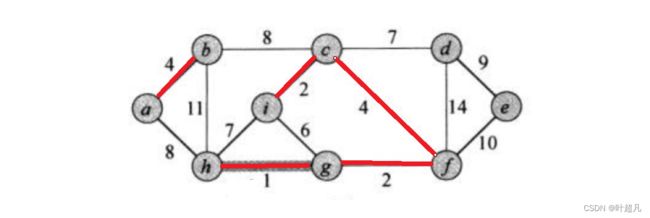
接下来权值最小的边就是ig它的权值为6，那能不能把它选上去呢？答案是不行的因为ig边的两侧节点为节点i和节点g这两个节点已经被连接起来了，如果还将ig选上去得话就会导致igcf成环，从而导致一个节点会漏选，同样得道理再小得边为ih和cd他们得权值为7，因为ih的两边已经被连接起来了所以不能再，那么这时就只能选择cd边

同样的道理ah和bc边也只能选着其中一条如果两条都选上了就会导致成环：

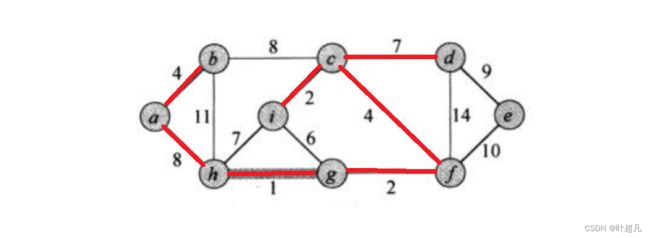
最后就是边de

那么操作到这里我们已经选择了8条边，并且这8条边刚好将9个节点都连接了起来，那么这就是Kruskal算法的原理。

2.Kruskal算法模拟实现

因为我们要比较每条的边的权值，还得判断每个节点是否已经被连接，所以我们这里得先创建一个类用来描述每条边，类中有两个变量用来记录两边节点的下标，还有个变量来记录边权值，因为要比较边的权值所以这里还得实现一个重载操作符>以方便后面类来比较大小，那么这里的代码如下：

struct edge
{
	edge(size_t srci, size_t dest, const W& w)
		:_srci(srci)
		,_dest(dest)
		,_w(w)
	{}
	size_t _srci;
	size_t _dest;
	W _w;
	bool operator>(const edge& e) const
	{
		return _w > e._w;
	}
};

因为Kruskal函数的作用是得到最小生成树，所以该函数的参数就是一个图类型的引用，在函数里面先对参数内部的数据进行修改就赋值为本图的顶点集合和下标和元素的对应集合，然后将内部的二维数组进行扩容并将里面的元素全部赋值成为MAX_W，那么这里的代码如下：

typedef Group< V,  W, MAX_W , Direction > self;
W Kruskal(self& minTree)
{
	minTree._vIndexMap = _vIndexMap;
	minTree._vertexs = _vertexs;
	minTree._matrix.resize(_matrix.size());
	for (int i = 0; i < _matrix.size(); i++)
	{
		minTree._matrix[i].resize(_matrix.size());
	}
}

因为要从很多的边里面选取最小的边出来，所以这里得创建一个优先级队列，队列里面存储的是边的集合，因为每次要选取的是权值最小的，所以实例化优先级队列的时候得用greater，创建完队列之后就要往队列里面插入数据，创建一个嵌套的for循环，在循环内部依次遍历本图的二维数组，因为这里是无向图可能会如果无脑循环的话会出现重复边的情况，所以这里我们就以对角线的方式来进行插入，那么这里的代码如下：

typedef Graph< V,  W, MAX_W , Direction > self;
W Kruskal(self& minTree)
{
	minTree._vIndexMap = _vIndexMap;
	minTree._vertexs = _vertexs;
	minTree._matrix.resize(_matrix.size());
	for (int i = 0; i < _matrix.size(); i++)
	{
		minTree._matrix[i].resize(_matrix.size());
	}
	priority_queue<edge, vector<edge>, greater<edge>> minque;
	for (int i = 0; i < _matrix.size(); i++)
	{
		for (int j = 0; j < i; j++)
		{
			if (_matrix[i][j] != MAX_W)
			{
				minque.push(edge(i, j, _matrix[i][j]));
			}
		}
	}

因为选取的边可能会出现成环的情况，所以我们这里还得创建一个并查集来帮助我们判断选出来的边是否会组成环，并查集的代码如下：

class UnionFindSet
{
public:
	UnionFindSet(int size)
		: _set(size, -1)
	{}

	size_t FindRoot(int x)
	{
		while (_set[x] >= 0)
			x = _set[x];

		return x;
	}

	void Union(int x1, int x2)
	{
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);

		if (root1 != root2)
		{
			_set[root1] += _set[root2];
			_set[root2] = root1;
		}
	}

	size_t SetCount()
	{
		size_t count = 0;
		for (size_t i = 0; i < _set.size(); ++i)
		{
			if (_set[i] < 0)
				count++;
		}

		return count;
	}

private:
	std::vector<int> _set;
};

创建一个并查集的对象将其容量设定为顶点的个数，再创建一个W类型的变量用来记录生成树的权值为多少，再创建一个变量i来记录当前选出来的边的个数，最后创建一个while循环来不停的选取边的，当边的个数为顶点的个数-1，或者优先级队列里面的元素为空时就结束选边，那么这里的代码就如下：

size_t i = 1;
W total = W();
UnionFindSet ufs(_vertexs.size());
while (i < _vertexs.size() && !minque.empty())
{
}

在循环里面先记录堆顶的元素，然后删除堆顶的元素，如果当前边的两个顶点的根节点不相同的话就可以添加边，并将边的两个顶点进行合并，最后让i的值加一让total的值加一，那么这里的代码如下：

size_t i = 1;
W total = W();
UnionFindSet ufs(_vertexs.size());
while (i < _vertexs.size() || !minque.empty())
{
	edge tmp = minque.top();
	minque.pop();
	if (ufs.FindRoot(tmp._dest) != ufs.FindRoot(tmp._srci))
	{
		minTree._AddEdge(tmp._srci, tmp._dest,tmp._w);这里注意调用的是哪个add函数
		ufs.Union(tmp._srci, tmp._dest);
		total += tmp._w;
		++i;
	}
}

循环结束之后就要判断一下，如果i的值等于顶点的个数就表明所有的边都已经找到了这时就可以直接返回total的值，如果不等于就表明当前图没有最小生成树我们就返回W类型的默认构造，那么完整的代码就如下：

struct edge
{
	edge(size_t srci, size_t dest, const W& w)
		:_srci(srci)
		,_dest(dest)
		,_w(w)
	{}
	size_t _srci;
	size_t _dest;
	W _w;
	bool operator>(const edge& e) const
	{
		return _w > e._w;
	}
};
typedef Graph< V,  W, MAX_W , Direction > self;
W Kruskal(self& minTree)
{
	minTree._vIndexMap = _vIndexMap;
	minTree._vertexs = _vertexs;
	minTree._matrix.resize(_matrix.size());
	for (int i = 0; i < _matrix.size(); i++)
	{
		minTree._matrix[i].resize(_matrix.size());
	}
	priority_queue<edge, vector<edge>, greater<edge>> minque;
	for (int i = 0; i < _matrix.size(); i++)
	{
		for (int j = 0; j < i; j++)
		{
			if (_matrix[i][j] != MAX_W)
			{
				minque.push(edge(i, j, _matrix[i][j]));
			}
		}
	}
	size_t i = 1;
	W total = W();
	UnionFindSet ufs(_vertexs.size());
	while (i < _vertexs.size() || !minque.empty())
	{
		edge tmp = minque.top();
		minque.pop();
		if (ufs.FindRoot(tmp._dest) != ufs.FindRoot(tmp._srci))
		{
			minTree._AddEdge(tmp._srci, tmp._dest,tmp._w);//这里注意调用的是哪个add函数
			ufs.Union(tmp._srci, tmp._dest);
			total += tmp._w;
			++i;
		}
	}
	if (i == _vertexs.size())
	{
		return total;
	}
	else
	{
		return W();
	}
}

代码实现完成之后于就可以用下面的代码来进行测试：

void test4()
{
	const char* str = "abcdefghi";
	Graph<char, int> g(str, strlen(str));
	g.AddEdge('a', 'b', 4);
	g.AddEdge('a', 'h', 8);
	g.AddEdge('b', 'c', 8);
	g.AddEdge('b', 'h', 11);
	g.AddEdge('c', 'i', 2);
	g.AddEdge('c', 'f', 4);
	g.AddEdge('c', 'd', 7);
	g.AddEdge('d', 'f', 14);
	g.AddEdge('d', 'e', 9);
	g.AddEdge('e', 'f', 10);
	g.AddEdge('f', 'g', 2);
	g.AddEdge('g', 'h', 1);
	g.AddEdge('g', 'i', 6);
	g.AddEdge('h', 'i', 7);
	Graph<char, int> kminTree;
	cout << "Kruskal:" << g.Kruskal(kminTree) << endl;
	kminTree.print();
}

为了方便我们查看运行的结果我们可以在添加边的时候打印这么一句话：

cout << _vertexs[tmp._srci] << "-" << _vertexs[tmp._dest] << ":" << _matrix[tmp._srci][tmp._dest] << endl;

那么这里的运行结果如下：

可以看到选择边的结构跟我们预期的是一致的，那么这就是克鲁斯卡尔算法。

3.prime算法原理

prime算法的原理和Kruskal算法的原理十分相似，它也是通过贪心算法来获取权值最小的边，但是这里的不同之处就在于Kruskal是从整体的角度来选取权值最小的边，而prime算法是给你一个顶点，把已经连接的顶点和没有连接的顶点看成两个集合，图中肯定存在一些边连接着这两个集合的点，那么prime就是从这些边里面选取权值最小的边，选取成功之后就将对应的顶点从未连接的顶点集合删除，添加到连接成功的顶点，那么这就是prime算法，我们可以通过下面的图片再来进行理解：

首先选取的节点为顶点a，那么这个时候我们就把a划入已连接点集合x，其余节点就划入未连接点集合y，因为x中只有一个顶点a，所以集合x和集合y相连接的边就是ab和ah，因为ab的权值为4小于ah的权值8，所以我们就选着边ab，因为ab连接了b点所以我们就y集合的b添加到x集合里面，因为b顶点加入到了x集合所以就得将原来ab边去掉把bh和bc边添加进来，此时的图片就是这样：

红色的线表示已经选着的线，而蓝色的线表示待选着的线，线bc和ah的权值相等且都小于bh并且不会构成环，所以这里可以把bc和ah都选上，选上之后c点和h点就纳入了x集合，这时因为x集合里面既有b节点和h节点所以此时的bh就该从待选边中去掉，那么这里的图片如下：

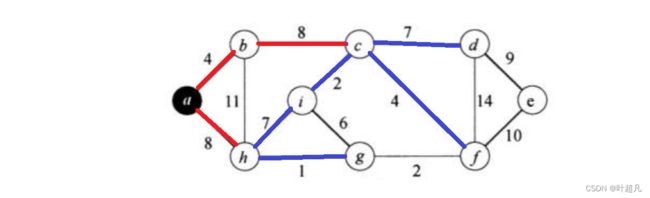
接下来选着的边就是ci

接着就是cf

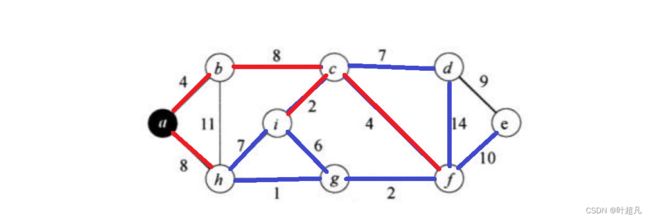
然后就是gf

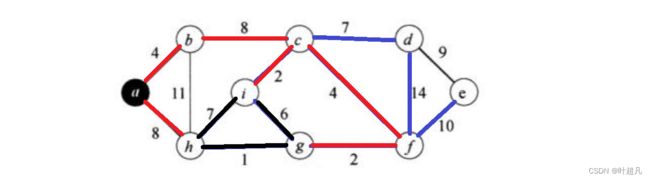
接着就是cd

最后就是dc

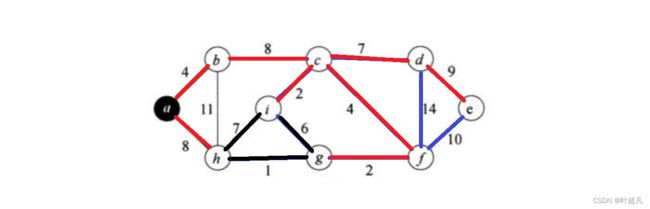
那么这就是prime的实现过程，接下我们来看看如何实现prime算法。

4.prim算法模拟实现

首先prime函数需要两个参数一个参数表示最小生成树另外一个参数表示起始元素，那么这里的代码如下：

W prim(self& minTree, const W&)
{

}

这里也是相同的道理在函数开始时先对minTree的值进行赋值，顶点的集合和下标对应的集合与本类相同，然后将二维数组的长度也改成与本对象相同并将里面的每一个值都赋值成为MAX_W，那么这里的代码如下：

W prim(self& minTree, const W& src)
{
	minTree._vIndexMap = _vIndexMap;
	minTree._vertexs = _vertexs;
	minTree._matrix.resize(_vertexs.size());
	for (int i = 0; i < _vertexs.size(); i++)
	{
		minTree._matrix[i].resize(_matrix.size());
	}
}

因为要不断的比较边的大小，所以这里还得创建一个优先级队列，因为要判断选着边的数量是否达标所以再创建一个变量用来记录边的个数，因为我们要判断选取的边是否来自于同一个结合所以这里还得创建一个set对象用来标识哪些节点我们已经遍历过了，然后我们就将找到元素src的下标并将该元素入set，然后创建一个for循环将与src相连的所有边全部都添加进优先级队列里面，那么这里的代码就如下：

W prim(self& minTree, const W& src)
{
	minTree._vIndexMap = _vIndexMap;
	minTree._vertexs = _vertexs;
	minTree._matrix.resize(_vertexs.size());
	for (int i = 0; i < _vertexs.size(); i++)
	{
		minTree._matrix[i].resize(_matrix.size());
	}
	size_t i = 1;//记录边的个数
	priority_queue<edge, vector<edge>, greater<edge>> minque;//记录最小边
	set<size_t> inset;
	size_t locate = GetVertexIndex(src);
	inset.insert(locate);
	for (int j = 0; j < _vertexs.size(); j++)
	{
		if (_matrix[locate][j] != MAX_W)
		{
			minque.push(edge(locate, j, _matrix[locate][j]));
		}
	}
}

然后我们就创建while循环记录堆顶元素并删除元素然后判断数据的两端是否都在set容器里面，如果都在的话就不执行任何内容接着循环，循环结束的条件就是优先级队列的元素为空或者选好了n-1条边，那么这里的代码如下：

while (i < _vertexs.size() || !minque.empty())
{
	edge tmp = minque.top();
	minque.pop();
	if (inset.find(tmp._dest) == inset.end() || inset.find(tmp._srci) == inset.end())
	{
		
	}
}

if语句里面就可以调用_add函数添加边，并且把total的值也加上对应边的权值，然后通过for循环将于desti顶点相连并且不在set对象里面的边全部都添加进去，最后将dest也添加进去set里面，那么这里的代码如下：

while (i < _vertexs.size() || !minque.empty())
{
	edge tmp = minque.top();
	minque.pop();
	if (inset.find(tmp._dest) == inset.end() || inset.find(tmp._srci) == inset.end())
	{
		cout << _vertexs[tmp._srci] << "-" <<_vertexs[tmp._dest] << ":" << _matrix[tmp._srci][tmp._dest] << endl;
		minTree._AddEdge(tmp._srci, tmp._dest, _matrix[tmp._srci][tmp._dest]);
		total += _matrix[tmp._srci][tmp._dest];
		++i;
		inset.insert(tmp._dest);
		for (int j = 0; j < _vertexs.size(); j++)
		{
			if (_matrix[tmp._dest][j] != MAX_W && inset.find(j) == inset.end())
			{
				minque.push(edge(tmp._dest,j,_matrix[tmp._dest][j]));
			}
		}
	}
}

最后判断一下选着的边的数目是否为n-1，如果为n-1的话就返回total的值，如果不为的话就返回w的默认构造，那么这里的代码就如下：

W prim(self& minTree, const W& src)
{
	minTree._vIndexMap = _vIndexMap;
	minTree._vertexs = _vertexs;
	minTree._matrix.resize(_vertexs.size());
	for (int i = 0; i < _vertexs.size(); i++)
	{
		minTree._matrix[i].resize(_matrix.size());
	}
	size_t i = 1;//记录边的个数
	priority_queue<edge, vector<edge>, greater<edge>> minque;//记录最小边
	set<size_t> inset;
	size_t locate = GetVertexIndex(src);
	inset.insert(locate);
	for (int j = 0; j < _vertexs.size(); j++)
	{
		if (_matrix[locate][j] != MAX_W)
		{
			minque.push(edge(locate, j, _matrix[locate][j]));
		}
	}
	inset.insert(locate);
	W total = W();
	while (i < _vertexs.size() || !minque.empty())
	{
		edge tmp = minque.top();
		minque.pop();
		if (inset.find(tmp._dest) == inset.end() || inset.find(tmp._srci) == inset.end())
		{
			cout << _vertexs[tmp._srci] << "-" <<_vertexs[tmp._dest] << ":" << _matrix[tmp._srci][tmp._dest] << endl;
			minTree._AddEdge(tmp._srci, tmp._dest, _matrix[tmp._srci][tmp._dest]);
			total += _matrix[tmp._srci][tmp._dest];
			++i;
			inset.insert(tmp._dest);
			for (int j = 0; j < _vertexs.size(); j++)
			{
				if (_matrix[tmp._dest][j] != MAX_W && inset.find(j) == inset.end())
				{
					minque.push(edge(tmp._dest,j,_matrix[tmp._dest][j]));
				}
			}
		}
	}
	if (inset.size() == _vertexs.size())
	{
		return total;
	}
	else
	{
		return W();
	}
}

我们可以用下面的代码来进行测试：

void test4()
{
	const char* str = "abcdefghi";
	Graph<char, int> g(str, strlen(str));
	g.AddEdge('a', 'b', 4);
	g.AddEdge('a', 'h', 8);
	g.AddEdge('b', 'c', 8);
	g.AddEdge('b', 'h', 11);
	g.AddEdge('c', 'i', 2);
	g.AddEdge('c', 'f', 4);
	g.AddEdge('c', 'd', 7);
	g.AddEdge('d', 'f', 14);
	g.AddEdge('d', 'e', 9);
	g.AddEdge('e', 'f', 10);
	g.AddEdge('f', 'g', 2);
	g.AddEdge('g', 'h', 1);
	g.AddEdge('g', 'i', 6);
	g.AddEdge('h', 'i', 7);
	Graph<char, int> kminTree;
	cout << "Kruskal:" << g.Kruskal(kminTree) << endl;
	kminTree.print();
	Graph<char, int> pminTree;
	cout << "Prim:" << g.prim(pminTree, 'a') << endl;
	pminTree.print();
}

代码的运行结果如下：

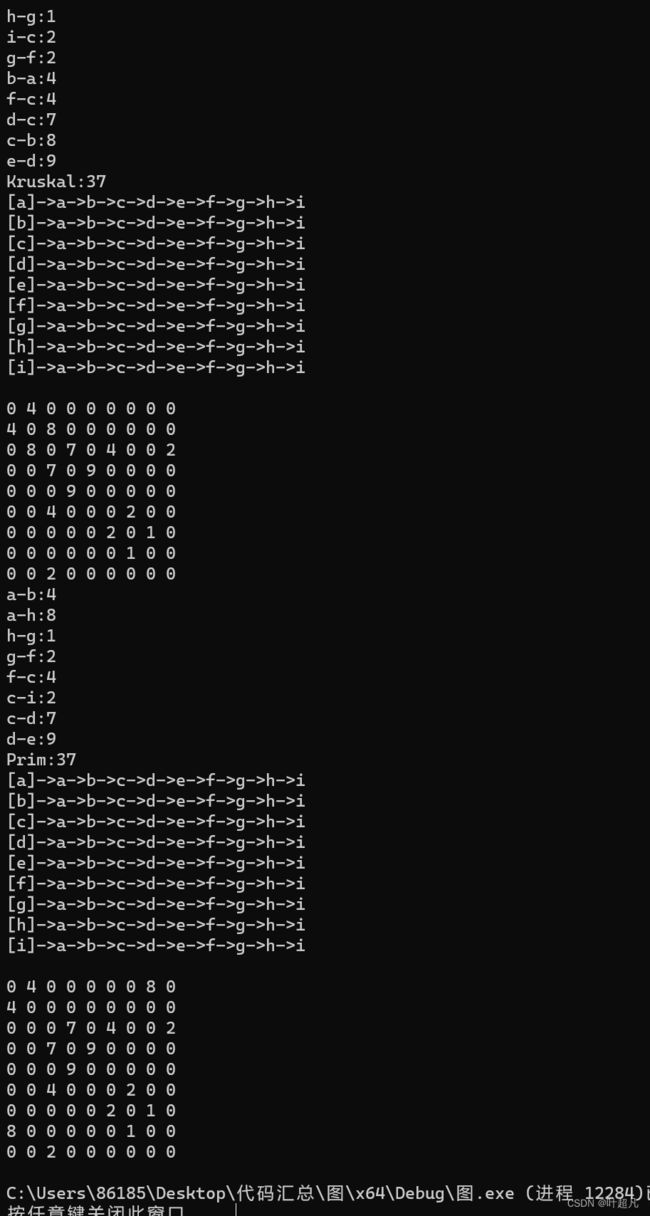
大家仔细地对比一下便可以看到这里地运行结果是正确的，并且得到的结果跟Kruskal算法不一样。

五.最短路径

最短路径问题：从在带权有向图G中的某一顶点出发，找出一条通往另一顶点的最短路径，最短也就是沿路径各边的权值总和达到最小。那么为了解决这个问题我们下面就提供了三个算法。

1.Dijkstra算法原理

Dijkstra算法就适用于解决带权重的有向图上的单源最短路径问题，同时算法要求图中所有边的权重非负。一般在求解最短路径的时候都是已知一个起点和一个终点，所以使用Dijkstra算法求解过后也就得到了所需起点到终点的最短路径。那么接下来我们就通过跟随着题目来讲解这个算法的原理，首先图片长成这样：

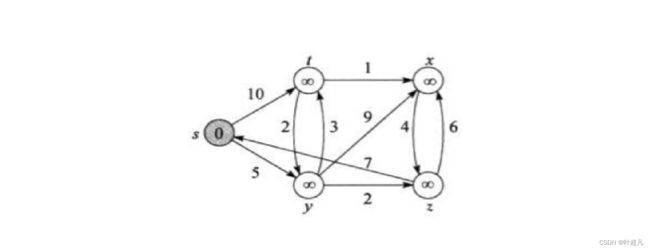
Dijkstra的原理就是通过贪心算法每次更新节点后选着路径最短的节点，然后再由这个节点连接的边更新其他的节点，s点是起点所以s点可以通过两条边确定顶点t和y的路径值分别为5和10，因为5比较小所有y点就确定了

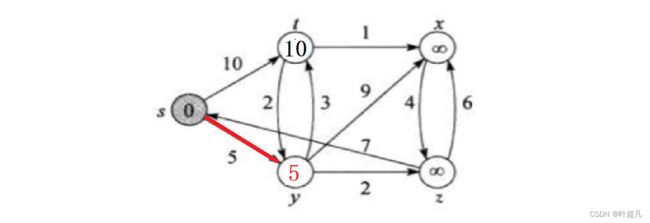
然后就根据y点根性其他相连节点的路径值，也就是t点 x点和z点，
因为z点的路径值最小所以z点也就确定了，然后就可以根绝z点的值更新与之相连的节点，因为z点的路径为7而xz的权值为6他们相加的值为13比x小，所以就将x的值更新一下变成13

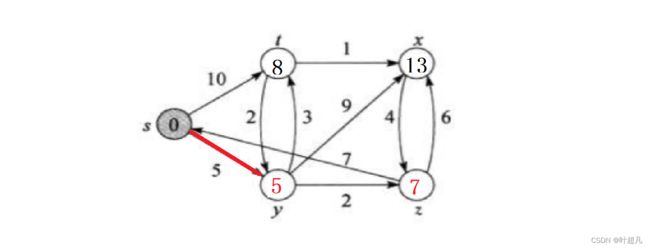
更新完之后就来确定下一个节点，因为t节点的路劲最小所以这个节点也就确定了，然后再用它连接的节点进行判断8加1小于13，所以就将x的节点修改成为9，因为x节点是最后一个节点所以它的路径也就确定了：

那么这就是该算法的原理，通过贪心选着路径最小的节点，然后由该节点来更新其他节点的路径然后不停的循环直到所有的节点都被确定。

2.Dijkstra算法模拟实现

首先这个函数需要两个vector类型的参数第一个参数用来存储到每个节点的最小路径，第二个参数用来表示最小路径中每个节点的父节点是谁，那么这里的代码如下：

void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)
{

}

在函数的开始将两个对象的长度都赋值为顶点的个数，然后得到src元素的下标并将pPath对象中的该下标元素赋值为下标的值，将dist数组中该下标的值赋值为0，那么这里的代码如下：

void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)
{
	dist.resize(_vertexs.size(), MAX_W);
	pPath.resize(_vertexs.size(), -1);
	size_t locate = GetVertexIndex(src);
	dist[locate] = 0;
	pPath[locate] = locate;
}

然后我们就要创建一个数组用来标记哪些顶点已经被确定了，然后我们创建一个for循环，因为只需要n次我们就可以确定该节点到所有节点的最小路径，所以这里循环的次数就是节点的个数，然后循环内部我们就创建一个变量min用来记录没有被确定且路径最小的节点，再创建一个变量用来记录该节点的下标，然后通过for循环加上if语句来找到这样的节点，那么这里代码如下：

void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)
{
	dist.resize(_vertexs.size(), MAX_W);
	pPath.resize(_vertexs.size(), -1);
	size_t locate = GetVertexIndex(src);
	dist[locate] = 0;
	pPath[locate] = locate;
	vector<bool> s(_vertexs.size(), false);
	for (int i = 0; i < _vertexs.size(); i++)
	{
		W min = MAX_W;//记录更新后的最小权值点
		int u = 0;//记录该点的下标
		for (int j = 0; j < _vertexs.size(); j++)
		{
			if (min > dist[j]&&s[j]==false)
			{
				min = dist[j];
				u = j;
			}
		}
		s[u] = true;
	}
}

找到这个顶点之后就可以再创建一个for循环将该节点与其他节点连接的连接的路径进行更新，如果目标节点没有确定并且路径的值小于该节点加上边的权值的话就进行根性并修改其父路径的值，那么这里代码如下：

void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)
{
	dist.resize(_vertexs.size(), MAX_W);
	pPath.resize(_vertexs.size(), -1);
	size_t locate = GetVertexIndex(src);
	dist[locate] = 0;
	pPath[locate] = locate;
	vector<bool> s(_vertexs.size(), false);
	for (int i = 0; i < _vertexs.size(); i++)
	{
		W min = MAX_W;//记录更新后的最小权值点
		int u = 0;//记录该点的下标
		for (int j = 0; j < _vertexs.size(); j++)
		{
			if (min > dist[j]&&s[j]==false)
			{
				min = dist[j];
				u = j;
			}
		}
		s[u] = true;
		for (int j = 0; j < _vertexs.size(); j++)
		{
			if (_matrix[u][j] != MAX_W && s[j] == false)
			{
				if (dist[u] + _matrix[u][j] < dist[j])
				{
					dist[j] = dist[u] + _matrix[u][j];
					pPath[j] = u;
				}
			}
		}

	}
}

为了方便我们的测试我们还可以添加一个打印函数，这个函数的原理和查并集差不多这里就不多说直接看代码：

void PrintShortPath(const V& src, const vector<W>& dist, const vector<int>& pPath)
{
	size_t srci = GetVertexIndex(src);
	size_t n = _vertexs.size();
	for (size_t i = 0; i < n; ++i)
	{
		if (i != srci)
		{
			// 找出i顶点的路径
			vector<int> path;
			size_t parenti = i;
			while (parenti != srci)
			{
				path.push_back(parenti);
				parenti = pPath[parenti];
			}
			path.push_back(srci);
			reverse(path.begin(), path.end());

			for (auto index : path)
			{
				cout << _vertexs[index] << "->";
			}
			cout << dist[i] << endl;
		}
	}
}

我们可以用下面的代码来进行测试：

void test5()
{
	const char* str = "syztx";
	Graph<char, int, INT_MAX, true> g(str, strlen(str));
	g.AddEdge('s', 't', 10);
	g.AddEdge('s', 'y', 5);
	g.AddEdge('y', 't', 3);
	g.AddEdge('y', 'x', 9);
	g.AddEdge('y', 'z', 2);
	g.AddEdge('z', 's', 7);
	g.AddEdge('z', 'x', 6);
	g.AddEdge('t', 'y', 2);
	g.AddEdge('t', 'x', 1);
	g.AddEdge('x', 'z', 4);
	vector<int> dist;
	vector<int> parentPath;
	g.Dijkstra('s', dist, parentPath);
	g.PrintShortPath('s', dist, parentPath);
}

代码的执行结果如下：

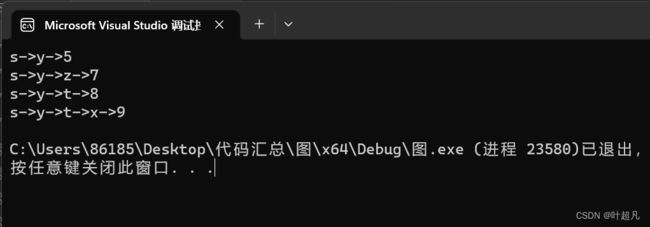
跟我们上面分析的一模一样，那么这就是Dijkstra的模拟实现。

3.再探原理和缺陷分析

Dijkstra算法在面对具有负权值的边时可能会出现问题，这个算法的思路就是将节点分为两类一类是最小路径已经确定的节点我们把这类称为x类，一类是最小路径没有确定的节点我们把这类称为y类，x类节点存在多条节路径通向y类节点，比如说x类中的中存在10个节点这10个节点一共20条路径通往y类，y类存在8个节点，那么我们就要比较这20条路径抵达8个节点中的最小路径，最小路径确定之后我们就可以将这个路径的目标节点由y类转换成为x类，为什么？原因1：这个节点是由x类转换过来的，x类中每个节点的最小路径都已经确定了，由x类转换过来的路径一定比y类的节点转换过来的路径要更小，因为y类本身就没有确定其次y类中的所有路径一定是比x类要大。原因二：这里选着的是更新之后y类所有节点中路径最小的节点，而且这里的更新是用的是所有路径进行更新，当这个节点的路径确定之后不会存在第二个条路径跟小的情况，所以可以将他归为x类，那么这就是Dijkstra的原理，那为什么面对存在负权值的路径这个算法就不能用了呢？我们来看上面的原因一：我们说从x类中挑选的路径一定比从y类挑选的路径要大，因为x要到y1才能抵达y2，y1到y2的值为正值而y2本身就比y1小，所以可以将y类的最小节点归为x类，如果出现权值为负数的边的话？y1到y2的值一定比x类节点到y2的值大吗？就不一定了吧，所以这个时候就不能将y类路径最小的节点归为x类，所以Dijkstra算法就失效了，那么面对权值为负数的图要想获取最小路径的话就得使用Bellman-Ford算法。

4.Bellman-Ford算法原理

Dijkstra算法是每次确定一个节点，可是因为负权值的出现导致无法根据x类节点连接出来的边来确定y节点，所以这个算法就是暴力的将每条边的所能达到节点的路径都进行一下更新，如果出现节点更小的值时就修改当前的当前节点的值，比如说下面的图片：

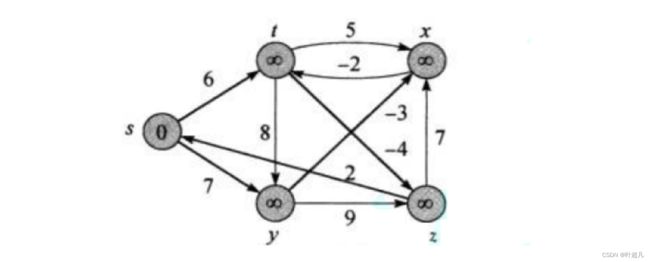
首先更新的是s节点连接的边，更新之后就变成了下面这样：

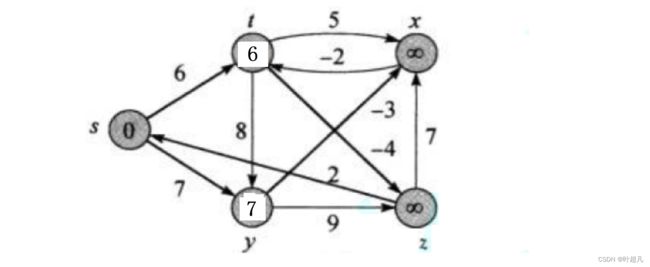
节点s更新完之后就要t和y节点连接的所有节点：

然后接着更新z节点连接的边和x节点连接的边，那么这里的图片就变成下面这样：

我们将每个节点连接的边都更新了一遍，得到的图片就是上面这样，但是这里很明显存在一个问题t可以通过权值为-4的边走到z使得z的路径为-2，而根据上面的思路我们得到z的值为2，这里很明显就有问题，出现问题的原因是这里对所有的节点只更新了一次，先由前面的节点来更新后面的节点，但是更新后面的节点也会影响前面的节点啊，所以就出现问题，解决问题的方法就是多更新几次，我们假设每次更新都有一个节点的值会因为后面的节点而改变，那么最多就会有n个节点发生改变，那么循环的次数就是节点的数目，那么这就是Bellman-Ford算法的原理。

5.Bellman-Ford算法模拟实现

首先函数需要三个参数两个vector类型的参数用来记录路径最小值和父路径的下标，一个W类型的参数用来记录起始点元素，然后在函数的开始将vector对象进行初始化，那么这里的代码如下：

bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)
{
	size_t N = _vertexs.size();
	size_t locate = GetVertexIndex(src);
	dist.resize(N, MAX_W);
	pPath.resize(N, -1);
	dist[locate] = W();
	pPath[locate] = locate;
}

然后创建一个嵌套的循环变量每个节点的每条边，如果出现更小节点的情况就对其进行顶点的值和顶点的父顶点的值进行更新，那么这里的代码如下：

bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)
{
	size_t N = _vertexs.size();
	size_t locate = GetVertexIndex(src);
	dist.resize(N, MAX_W);
	pPath.resize(N, -1);
	dist[locate] = W();
	pPath[locate] = locate;
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{
			if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
			{
				dist[j] = dist[i] + _matrix[i][j];
				pPath[j] = i;
			}
		}
	}
}

这里是对所有的节点进行一次更新因为后面更新的节点可能会影响前面的节点，所以这里还得循环多次，又因为不是所有的图都得更新顶点数目次，所以再添加一个变量用来标记，那么这里的代码如下：

bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)
{
	size_t N = _vertexs.size();
	size_t locate = GetVertexIndex(src);
	dist.resize(N, MAX_W);
	pPath.resize(N, -1);
	dist[locate] = W();
	pPath[locate] = locate;
	for (int size = 0; size < N; size++)
	{
		bool flag = false;
		for (int i = 0; i < N; i++)
		{
			for (int j = 0; j < N; j++)
			{
				if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
				{
					flag = true;
					dist[j] = dist[i] + _matrix[i][j];
					pPath[j] = i;
				}
			}
		}
		if (flag == false)
		{
			break;
		}
	}
}

因为可能会出现负闭环的问题所以循环结束之后我们得判断一下如果已经能够更新节点的值就直接返回false，如果不能就返回true，那么为了方便后面的查看这里还得添加标记语句，那么这里的代码如下：

bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)
{
	size_t N = _vertexs.size();
	size_t locate = GetVertexIndex(src);
	dist.resize(N, MAX_W);
	pPath.resize(N, -1);
	dist[locate] = W();
	pPath[locate] = locate;
	for (int size = 0; size < N; size++)
	{
		bool flag = false;
		cout << "更新第:" << size << "轮" << endl;
		for (int i = 0; i < N; i++)
		{
			for (int j = 0; j < N; j++)
			{
				if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
				{
					flag = true;
					cout << _vertexs[i] << "->" << _vertexs[j] << ":" << _matrix[i][j] << endl;	
					dist[j] = dist[i] + _matrix[i][j];
					pPath[j] = i;
				}
			}
		}
		if (flag == false)
		{
			break;
		}
	}
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{
			if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
			{
				return false;
			}
		}
	}
	return true;	
}

我们可以用下面的代码来进行测试：

void test6()
{
	const char* str = "syztx";
	Graph<char, int, INT_MAX, true> g(str, strlen(str));
	g.AddEdge('s', 't', 6);
	g.AddEdge('s', 'y', 7);
	g.AddEdge('y', 'z', 9);
	g.AddEdge('y', 'x', -3);
	g.AddEdge('z', 's', 2);
	g.AddEdge('z', 'x', 7);
	g.AddEdge('t', 'x', 5);
	g.AddEdge('t', 'y', 8);
	g.AddEdge('t', 'z', -4);
	g.AddEdge('x', 't', -2);
	vector<int> dist;
	vector<int> parentPath;
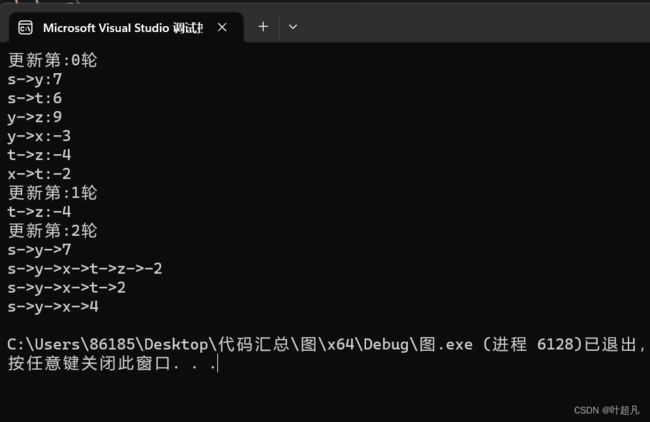
	if (g.BellmanFord('s', dist, parentPath))
	{
		g.PrintShortPath('s', dist, parentPath);
	}
	else
	{
		cout << "存在负权回路" << endl;
	}
}

代码的运行结果如下：

6.Floyd-Warshall算法原理

如果要求解任意两点的最小路径时就可以使用Floyd-Warshall算法和Dijkstra，这个算法的时间复杂度为n的三次方，而Bellman-Ford算法也可以求任意两点的最小路径但是它来求的话时间复杂度就会变成n的四次方，而Dijkstra算法不能存在负劝边，那么接下来我们就讲解一下这个算法的原理，首先这个算法将节点之间的关系分为两种情况：一种时直接相连的节点也就是两个节点之间没有其他节点，另外一种就是节点和节点之间通过其他节点相连，那么两个节点可能即属于第一种情况，也可能属于第二种情况，如果属于第一种情况他们之间的路径就为那个边的权值，如果属于第二种情况这两点之间的路径就等于中间节点的最后一个节点的路径加上该点和目标点边的边的权值，这个中间点存在多个那么具体是哪几个我们不知道，所以这里得一个一个的遍历并且记录每次得到最小值，那么这里实际上就是一个动态规划的过程：

那么接下来我们来看看如何实现这个代码。

7.Floyd-Warshall算法模拟实现

因为这里要记录任意两点的最短路径，所以参数得变成两个二维数组，然后函数的开始对数组的元素进行初始化：

void FloydWarshall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath)
{
	size_t N = _vertexs.size();
	vvDist.resize(N);
	vvpPath.resize(N);
	for (int i = 0; i < N; i++)
	{
		vvDist[i].resize(N,W();
		vvpPath[i].resize(N,-1);
	}
}

如果有两个顶点直接相连那么就将这个边的权值进行赋值到vvDist里面，那么这里的代码如下：

void FloydWarshall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath)
{
	size_t N = _vertexs.size();
	vvDist.resize(N);
	vvpPath.resize(N);
	for (int i = 0; i < N; i++)
	{
		vvDist[i].resize(N,MAX_W);
		vvpPath[i].resize(N,-1);
	}
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{
			if (_matrix[i][j] != MAX_W)
			{
				vvDist[i][j] = _matrix[i][j];
				vvpPath[i][j] = i;
			}
			if (i == j)
			{
				vvDist[i][j] = W();
			}
		}
	}
}

然后创建一个三层循环，外层循环表示中间可能存在的节点，这个循环的次数表示可能出现节点的下标，内部的两个循环表示任意两个节点间的距离，所以加在一起就表示任意两个节点之间可能存在着的节点：

for (int k = 0; k < N; k++)//表示中的k个节点
{
	//内部的两层循环表示的任意的两个节点
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{

		}
	}
}

然后在循环内部我们就要进行判断，如果i号节点和k号节点相连，并且k号节点和j号节点相连的话我们就进行判断如果i到k的值加上k到j的值小于原来记录的值的话就进行更新，

for (int k = 0; k < N; k++)//表示中的k个节点
{
	//内部的两层循环表示的任意的两个节点
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{
			// k 作为的中间点尝试去更新i->j的路径
			if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W
				&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j])
			{
				vvDist[i][j] = vvDist[i][k] + vvDist[k][j];

				// 找跟j相连的上一个邻接顶点
				// 如果k->j 直接相连，上一个点就k，vvpPath[k][j]存就是k
				// 如果k->j 没有直接相连，k->...->x->j，vvpPath[k][j]存就是x

				vvpPath[i][j] = vvpPath[k][j];
			}
		}
	}
}

到这里到代码就实现完成了但是为了方便查看，我们还可以添加一些打印的信息那么完整的代码如下：

void FloydWarshall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath)
{
	size_t N = _vertexs.size();
	vvDist.resize(N);
	vvpPath.resize(N);
	for (int i = 0; i < N; i++)
	{
		vvDist[i].resize(N,MAX_W);
		vvpPath[i].resize(N,-1);
	}
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{
			if (_matrix[i][j] != MAX_W)
			{
				vvDist[i][j] = _matrix[i][j];
				vvpPath[i][j] = i;
			}
			if (i == j)
			{
				vvDist[i][j] = W();
			}
		}
	}
	for (int k = 0; k < N; k++)//表示中的k个节点
	{
		//内部的两层循环表示的任意的两个节点
		for (int i = 0; i < N; i++)
		{
			for (int j = 0; j < N; j++)
			{
				// k 作为的中间点尝试去更新i->j的路径
				if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W
					&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j])
				{
					vvDist[i][j] = vvDist[i][k] + vvDist[k][j];

					// 找跟j相连的上一个邻接顶点
					// 如果k->j 直接相连，上一个点就k，vvpPath[k][j]存就是k
					// 如果k->j 没有直接相连，k->...->x->j，vvpPath[k][j]存就是x

					vvpPath[i][j] = vvpPath[k][j];
				}
			}
		}
	}
	// 打印权值和路径矩阵观察数据
	for (size_t i = 0; i < N; ++i)
	{
		for (size_t j = 0; j < N; ++j)
		{
			if (vvDist[i][j] == MAX_W)
			{
				//cout << "*" << " ";
				printf("%3c", '*');
			}
			else
			{
				//cout << vvDist[i][j] << " ";
				printf("%3d", vvDist[i][j]);
			}
		}
		cout << endl;
	}
	cout << endl;
	for (size_t i = 0; i < N; ++i)
	{
		for (size_t j = 0; j < N; ++j)
		{
			//cout << vvParentPath[i][j] << " ";
			printf("%3d", vvpPath[i][j]);
		}
		cout << endl;
	}
	cout << "=================================" << endl;
}

然后我们可以用下面的代码来进行测试：

void test7()
{
	const char* str = "12345";
	Graph<char, int, INT_MAX, true> g(str, strlen(str));
	g.AddEdge('1', '2', 3);
	g.AddEdge('1', '3', 8);
	g.AddEdge('1', '5', -4);
	g.AddEdge('2', '4', 1);
	g.AddEdge('2', '5', 7);
	g.AddEdge('3', '2', 4);
	g.AddEdge('4', '1', 2);
	g.AddEdge('4', '3', -5);
	g.AddEdge('5', '4', 6);
	vector<vector<int>> vvDist;
	vector<vector<int>> vvParentPath;
	g.FloydWarshall(vvDist, vvParentPath);
	// 打印任意两点之间的最短路径
	for (size_t i = 0; i < strlen(str); ++i)
	{
		g.PrintShortPath(str[i], vvDist[i], vvParentPath[i]);
		cout << endl;
	}
}

代码的运行结果如下：

这个测试的原图如下：