c语言(函数)
目录
何为函数
库函数
自定义函数
二分查找数组下标
链式访问
函数的声明
函数定义
递归
正向打印数字
打印字符个数
使用临时变量
递归(不使用临时变量)
n的阶乘
一般形式
递归
斐波那契数
递归
正常做法
何为函数
在计算机科学中,子程序是一个大型程序中的某部分代码, 由一个或多个语句块组
成。它负责完成某项特定任务,而且相较于其他代 码,具备相对的独立性。
一般会有输入参数并有返回值,提供对过程的封装和细节的隐藏。这些代码通常被集成为软
件库。
函数分为库函数和自定义函数
库函数
- 库函数只提供函数名,参数,功能,返回类型,实现则由编译器厂商实现。
- 库函数的使用需要包含对应的头文件。
- c/c++库函数官网:https://cplusplus.com/
自定义函数
实际很多情况我们不能靠库函数解决,所以就诞生了自定义函数,我们可以自己实现内部细节和功能。
现在实现一个交换函数:
void Swap(int x, int y)
{
int z = 0;
z = x;
x = y;
y = z;
}运行结果:
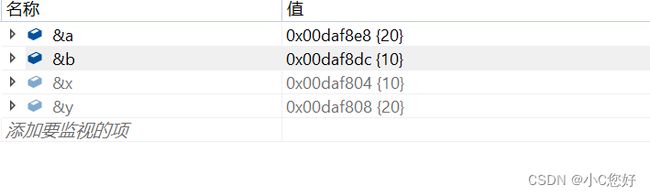
为什么没有实现交换功能呢?
我们可以看到它们的地址都不一样,所以没能实现交换,我们称传递的参数为实参,接收的参数为形参,形参是实参的拷贝,形参的建立与销毁只在调用函数的过程发生。所以它的交换只在函数体内。
void Swap(int* x, int* y)
{
int z = 0;
z = *x;
*x = *y;
*y = z;
}
int main()
{
int a = 0;
int b = 0;
scanf("%d %d", &a, &b);//输入
printf("交换前:a=%d b=%d\n", a, b);
//传地址,传址调用
Swap(&a, &b);
printf("交换后:a=%d b=%d\n", a, b);
return 0;
}我们传递地址,这样就可以实现交换功能了。
二分查找数组下标
我们利用一组数据有序的特点,这次我们试着用函数的方式封装二分查找这一功能。
找7,发现找不到,这是为什么呢?我们来看函数部分:
通过调试发现,这里的right始终为0,这就是问题所在了,在c语言中,数组的传参是传递的指针而非整个数组,这是因为可以通过首元素地址找到整个下组,从而减少了不必要的开销。
完整代码:
int binary_search(int *arr, int k,int right)
{
int left = 0;
while (left <= right)
{
int mid = (left + right) / 2;
if (arr[mid] > k)
{
right = mid - 1;
}
else if (arr[mid] < k)
{
left = mid + 1;
}
else
{
return mid;//找到了
}
}
return -1;//找不到
}
int main()
{
int arr[10] = { 1,2,3,4,5,6,7,8,9,10 };
int sz = sizeof(arr) / sizeof(arr[0]);
int k = 7;
int right = sizeof(arr) / sizeof(arr[0]);
int ret = binary_search(arr, k,sz);
if (-1 == ret)
printf("找不到\n");
else
printf("找到了,下标是:%d\n", ret);
}函数允许嵌套调用,不允许嵌套定义。
链式访问
链式访问就是一个函数的返回值作为另一个函数的参数,像链条一样串起来。
比如printf函数的返回值是字符的个数:
函数的声明
函数的声明一般是包含在.h文件里,用于综合性的工程里。
//函数定义
int Add(int x, int y);
int Add(int, int);如果我们创建一个add.h的头文件,里面写上函数的声明,我们可以这样包含达到使用我们自己的“库”的效果。
#include "add.h"当然,如果你不小心将函数的定义放在了main函数后,你也可以这样使用:
int main()
{
int Add(int, int);
Add(a,b);
return 0;
}
int Add(int a, int b)
{
//..
}函数定义
同理,我们可以把函数的定义放在.c文件里。
同时,要想不让人知道函数的具体实现过程,我们可以通过打包静态库的方式隐藏自己的函数文件。
递归
顾名思义,递归的核心是大事化小,通过一次一次迭代,达到最终效果的过程。
正向打印数字
我们知道反向打印4个数可以:
1234%10 = 4;
1234/10 = 123;
123%10 = 3;那正向怎么做呢,在知道我们可以轻松拿到它的末尾数字时,我们是不是可以反向思考一下?
123 (4)
12 (34)
1 (234)void Print(unsigned int n)//1
{
if (n > 9)
{
print(n / 10);
}
printf("%d ", n % 10);
}
void Print(unsigned int x)//2
{
if (x < 10)
{
printf("%d ", x);
}
else
{
Print(x / 10);
printf("%d ", x % 10);
}
}调用了4次函数,开辟了4次函数栈帧,在打印后返回上一层栈帧并销毁空间。
- 递归必须有限制条件
- 每次递归会逐渐靠近这个限制条件
打印字符个数
使用临时变量
int my_strlen(char* s)
{
int count = 0;
while (*s != '\0')
{
count++;
s++;
}
return count;
}递归(不使用临时变量)
同理,例如一个字符串abc拆分成1+bc,1+1+c,1+1+1+0的形式。
int my_strlen(char* str)
{
if (*str != '\0')
return 1 + my_strlen(str + 1);
else
return 0;
}注意这里最好不要用前置++,它改变了数组的地址。
n的阶乘
阶乘公式 :
- n<=1,1
- n>1,Fac(n-1) * n
一般形式
int Fac(int n)
{
int i = 0, ret = 1;
for (i = 1;i <= n; i++)
{
ret = ret * i;
}
return ret;
}递归
int Fac(int n)
{
if (n <= 1)
{
return 1;
}
else
return Fac(n - 1) * n;
}斐波那契数
1 1 2 3 5 8 13 .... 像这样前两个数加起来等于后一个数的数列叫做斐波那契数列。
递归
公式:
n<=2, n = 1
n>2, Fib(n-1) + Fib(n-2)
int Fib(int n)
{
if (n <= 2)
return 1;
else
return Fib(n - 1) + Fib(n - 2);
}测试:
测试发现计算一个稍微大点的数据半天计算不出来结果,可以得知递归的层次已经很深了,就像一张很深的数 一样。
正常做法
在数字超出两个时,我们可以用两个变量求和计算第三个变量,依次更新,达到想要的效果。
int Fib(int n)
{
int a = 1;
int b = 1;
int c = 0;
if (n <= 2)
{
return 1;
}
if (n > 2)
{
while(n>2)
{
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
}用这种方法几乎是一瞬间得出了结果,不过注意数据太大可能会超出范围。
总之,递归的使用需要我们多去总结和感悟,并选择最合适的方法 。