第 357 场力扣周赛题解

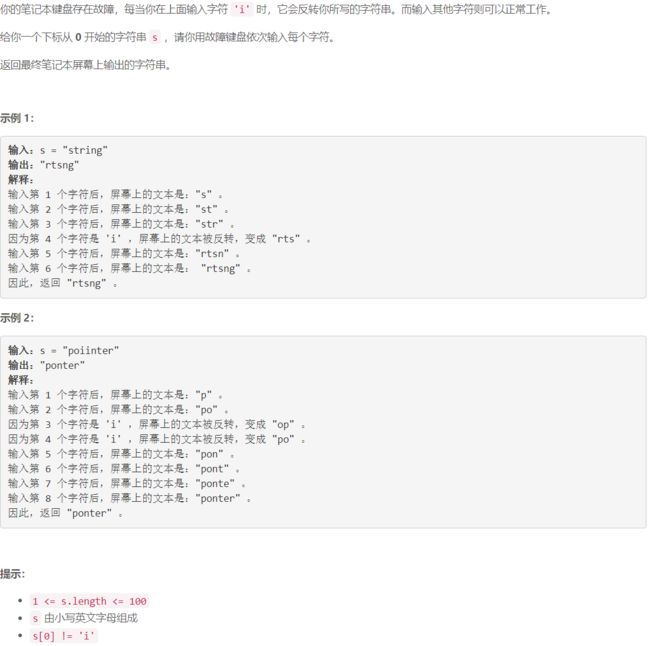
A 故障键盘

简单模拟

class Solution {
public:
    string finalString(string s) {
        string res;
        for (auto c: s)
            if (c != 'i')
                res.push_back(c);
            else
                reverse(res.begin(), res.end());
        return res;
    }
};

---

B 判断是否能拆分数组

区间dp：定义$p_{i,j}$表示子数组$nums[i,j]$能否满足条件地拆分为$j-i+1$个非空数组，$p_{i,j}$最多可由$p_{i+1,j}$和$p_{i,j-1}$转移，注意特判$nums[i,j]$为整个数组的情况。

class Solution {
public:
    bool canSplitArray(vector<int> &nums, int m) {
        int n = nums.size();
        int s[n + 1];//前缀和
        s[0] = 0;
        for (int i = 1; i <= n; i++)
            s[i] = s[i - 1] + nums[i - 1];
        int p[n][n];//1：可满足条件地拆分，0：不可满足条件地拆分
        for (int len = 1; len <= n; len++)
            for (int i = 0, j = i + len - 1; j < n; i++, j++) {
                if (len == 1)//长度为1满足条件
                    p[i][j] = 1;
                else//当前区间和>=m 或当前区间为整个数组，才可能可以满足条件地拆分
                    p[i][j] = s[j + 1] - s[i] >= m || len == n ? (p[i][j - 1] | p[i + 1][j]) : 0;
            }
        return p[0][n - 1];
    }
};

---

C 找出最安全路径

多源$bfs$+二分：以所有小偷所在位置为源点跑多源$bfs$，这样就求出了矩阵各个位置的安全系数，然后二分枚举答案，设当前枚举值为$res$，判断当前枚举值是否可行：通过$bfs$判断$(0,0)$与$(n-1,n-1)$之间是否存在这样的路径，使得该路径上任意位置的安全系数都不小于$res$。

class Solution {
public:
    int maximumSafenessFactor(vector<vector<int>> &grid) {
        int n = grid.size();
        int d[n][n];//记录位置的安全系数
        memset(d, -1, sizeof(d));//初始化未访问标志
        queue<pair < int, int> > q;
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                if (grid[i][j]) {//多源bfs的源点
                    d[i][j] = 0;
                    q.emplace(i, j);
                }
        int dr[4] = {1, -1, 0, 0};
        int dc[4] = {0, 0, 1, -1};
        while (!q.empty()) {//多源bfs
            auto [r, c] = q.front();
            q.pop();
            for (int k = 0; k < 4; k++) {
                int nr = r + dr[k];
                int nc = c + dc[k];
                if (nr < 0 || nr >= n || nc < 0 || nc >= n || d[nr][nc] != -1)
                    continue;
                d[nr][nc] = d[r][c] + 1;
                q.emplace(nr, nc);
            }
        }
        int l = 0, r = 2 * (n - 1);
        int vis[n][n];//记录是否在当前枚举值的bfs过程中访问过
        memset(vis, -1, sizeof(vis));
        while (l < r) {//二分枚举答案
            int res = (l + r + 1) / 2;
            queue<pair < int, int> > q;
            if (d[0][0] >= res) {//(0,0)为源点
                vis[0][0] = res;
                q.emplace(0, 0);
            }
            while (!q.empty()) {//bfs判断当前枚举值是否可行
                auto [r, c] = q.front();
                q.pop();
                if (r == n - 1 && c == n - 1)
                    break;
                for (int k = 0; k < 4; k++) {
                    int nr = r + dr[k];
                    int nc = c + dc[k];
                    if (nr < 0 || nr >= n || nc < 0 || nc >= n || d[nr][nc] < res || vis[nr][nc] == res)
                        continue;
                    vis[nr][nc] = res;//标记当前枚举值的bfs过程中已访问
                    q.emplace(nr, nc);
                }
            }
            if (vis[n - 1][n - 1] == res)
                l = res;
            else
                r = res - 1;
        }
        return l;
    }
};

---

D 子序列最大优雅度

堆+哈希：将$items$按利润降序排序，然后将前$k$个项目加入选择集合，然后枚举剩余的项目$items[i]$：

• 若$items[i]$的项目类别在选择集合中已有，则直接跳过该项目
• 若$items[i]$的项目类别没有在选择集合中
  • 若当前选择集合中存在出现次数大于1的项目，将其中利润最小的项目移出集合，同时将$items[i]$加入集合
  • 若当前选择集合中不存在出现次数大于1的项目，结束枚举

实现可以用堆来维护选择集合中利润最小的项目，用哈希表记录各个类别在当前选择集合中的出现次数。

class Solution {
public:
    long long findMaximumElegance(vector<vector<int>> &items, int k) {
        sort(items.begin(), items.end(), [](const vector<int> &a, const vector<int> &b) { return a[0] > b[0]; });//按利润降序排序
        unordered_map<int, int> cnt;
        long long s = 0;//选择集合中项目的利润和
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> minheap;
        for (int i = 0; i < k; i++) {
            minheap.emplace(items[i][0], items[i][1]);
            s += items[i][0];
            cnt[items[i][1]]++;
        }
        long long res = s + (long long) (cnt.size() * cnt.size());
        for (int i = k; i < items.size(); i++) {
            int pi = items[i][0], ci = items[i][1];
            if (cnt[ci])//当前项目类别在选择集合中已有
                continue;
            while (!minheap.empty() && cnt[minheap.top().second] == 1)
                minheap.pop();
            if (minheap.empty())//当前选择集合中不存在出现次数大于1的项目
                break;
            auto [top_pi, top_ci] = minheap.top();
            minheap.pop();
            cnt[top_ci]--;
            cnt[ci]++;
            s += pi - top_pi;
            res = max(res, s + (long long) (cnt.size() * cnt.size()));
        }
        return res;
    }
};