七大排序内容

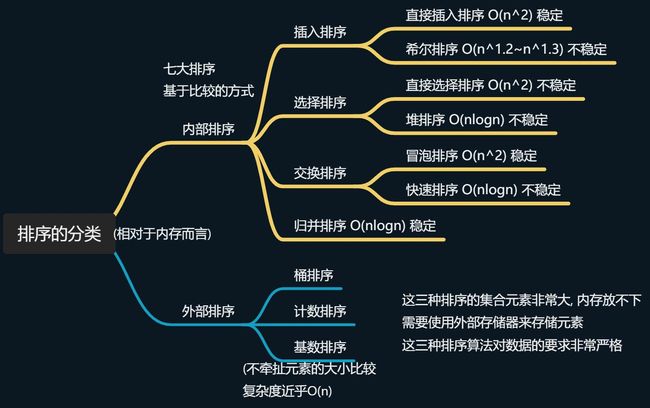
一. 排序的分类

二. 七大排序

直接选择排序

核心思路

每次在无序区间中选择最小值, 与无序区间的第一个元素交换, 直到整个数组有序
在选择排序中, 当无序区间只剩下一个元素时, 循环退出, 整个数组有序
选择排序不是一个稳定的排序算法

代码

// 选择排序
public static void selectionSort(int[] arr) {
    // 起始状态 : 有序区间[0..i)
    // 无序区间[i....n)
    for (int i = 0; i < arr.length - 1; i++) {
        // min指向的当前无序区间的最小值
        int min = i;
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[j] < arr[min]) {
                min = j;
            }
        }
        // 此时min一定指向无序区间最小值下标，换到无序区间的最开始位置
        swap(arr,i,min);
    }
}

插入排序

核心思路

每次从无序区间中选择第一个元素, 插入到有序区间的合适位置, 直到整个数组有序
插入排序在近乎有序的集合上性能非常好, 经常作为其他高阶排序的优化手段

代码

// 在数组arr[l..r]上进行插入排序
private static void insertionSort(int[] arr, int l, int r) {
    for (int i = l + 1; i <= r; i++) {
        for (int j = i; j > l && arr[j] < arr[j - 1]; j--) {
            swap(arr,j,j - 1);
        }
    }
}

`arr[j] < arr[j - 1]`写在循环体里面而不是括号里面, 那么判断条件只是j > l，即只要当前元素还没到达左边界，就一直向左遍历。这样的话，即使当前元素比前一个元素大，它也会一直向左移动，直到到达左边界或找到一个比它小的元素为止。这种方式虽然也可以实现排序，但效率可能会降低，因为它进行了更多的比较和交换操作。

希尔排序

核心思路

是对插入排序的优化, 借助插入排序在近乎有序的数组上性能很好的特性.
数组的元素越少, 这个数组越接近于有序状态
把原数组分成若干个子数组, 先把子数组调整为内部有序, 不断变大这个数组的长度, 最终当分组长度为1时, 整个数组接近有序, 最后来一次插入排序即可
例如:
9,1,2,5a,6,4,8,6,3,5b 先把原数组10个元素划分为5组 gap = n/2 = 5
=> [9,4] [1,8] [2,6] [5a,3] [7,5b] 排序一下
=> [4,9] [1,8] [2,6] [3,5a] [5b,7]
=> [4,1,2,3,5b,9,8,6,5a,7]
gap = gap/2 = 2
=> [4,2,5b,8,5a] [1,3,9,6,7] 排序一下
=> [2,4,5b,5a,8] [1,3,6,7,9]
=> [1,2,3,4,5b,5a,6,7,8,9]
gap = gap/2 = 1, 此时数组已经接近有序, 此时在整个数组是进行插入排序, 时间最佳
=> [1,2,3,4,5b,5a,6,7,8,9]

代码

// 希尔排序
public static void shellSort(int[] arr) {
    int gap = arr.length >> 1;
    while (gap > 1) {
        // 先按照gap分组，组内使用插入排序
        insertionSortByGap(arr,gap);
        gap = gap >> 1;
    }
    // 当gap == 1时，整个数组接近于有序，此时来一个插入排序
    insertionSortByGap(arr,1);
}

// 按照gap分组，组内的插入排序
private static void insertionSortByGap(int[] arr, int gap) {
    for (int i = gap; i < arr.length; i++) {
        for (int j = i; j - gap >= 0 && arr[j] < arr[j - gap] ; j -= gap) {
            swap(arr,j,j - gap);
        }
    }
}

归并排序

核心思路

步骤①: 先不断的将数组一分为二, 直到拆分后的子数组只剩下一个元素(当数组只有一个元素时, 天然有序)
步骤②: 不断地将两个连续的子数组合并成一个大数组, 直到整个数组合并完成(merge())

最核心的merge:

把两个有序的小数组合并成大数组, 然后这个大数组的左右两边可以看作两个小数组, 分别从这两个"虚拟的"小数组的左边扫描到右边, 并比较大小(用i, j当指针), 插入到原来真正的小数组(用k来当指针).
当i>mid代表小的都已经回填完毕, 剩下的就都是大的了(而且已经是有序的了), 所以一口气全部回填即可.
或者当j>r意味着大的都回填完毕, 把剩下小的回填即可(这种操作就不用再最后把新建的数组内容再copy会原来的数组, 直接边排序就变放回去了)

涉及到的方法

System.arraycopy(arr1, l1, arr2, l2, len)
arr1: 原数组名称
l1: 需要拷贝的原数组开始位置
arr2: 目标数组的名称
l2: 目标数组的开始位置
len: 组要拷贝的长度

代码

// 归并排序
public static void mergeSort(int[] arr) {
    mergeSortInternal(arr,0,arr.length - 1);
}
// 在arr[l...r]进行归并排序
private static void mergeSortInternal(int[] arr, int l, int r) {
    // base case
    // 优化2.小数组(64个元素以内)直接使用插入排序
    if (r - l <= 64) {
        insertionSort(arr,l,r);
        return;
    }
    // mid = (l + r) / 2
    int mid = l + ((r - l) >> 1);
    // 先将原数组一分为二，在子数组上先进行归并排序
    mergeSortInternal(arr,l,mid);
    mergeSortInternal(arr,mid + 1,r);
    // 此时两个子数组已经有序,将这两个子数组合并为原数组
    if (arr[mid] > arr[mid + 1]) {
        // 优化1.只有子数组1和子数组2存在元素的乱序才需要合并
        merge(arr,l,mid,r);
    }
}
// 在数组arr[l..r]上进行插入排序
private static void insertionSort(int[] arr, int l, int r) {
    for (int i = l + 1; i <= r; i++) {
        for (int j = i; j > l && arr[j] < arr[j - 1]; j--) {
            swap(arr,j,j - 1);
        }
    }
}

private static void merge(int[] arr, int l, int mid, int r) {
    // 创建一个大小为r - l + 1的与原数组长度一样的临时数组aux
    int[] aux = new int[r - l + 1];
    System.arraycopy(arr,l,aux,0,r - l + 1);
    // 两个子数组的开始索引
    int i = l,j = mid + 1;
    // k表示当前原数组合并到哪个位置
    for (int k = l; k <= r; k++) {
        if (i > mid) {
            // 子数组1全部拷贝完毕，将子数组2的所有内容协会arr
            arr[k] = aux[j - l];
            j ++;
        }else if (j > r) {
            // 子数组2全部拷贝完毕，将子数组1的剩余内容写回arr
            arr[k] = aux[i - l];
            i ++;
        }else if (aux[i - l] <= aux[j - l]) {
            // 稳定性
            arr[k] = aux[i - l];
            i ++;
        }else {
            arr[k] = aux[j - l];
            j ++;
        }
    }
}

应用

处理海量数据处理:
无论原始数据怎样都可以这样操作.
若有待排序数据100G, 但内存只有1G, 需要借助磁盘
先将数据等分为200份, 每份数据大小500M
先把小数据加载到内存, 使用内部排序(快排,归并), 将这200个小数据排序(子数组排序)
最后进行200路归并, 将200份文件写回到源文件(merge)

快速排序

核心思路

每次从无序数组中选取一个元素称为分区点(pivot), 将集合中所有=pivot的元素放在分区点的右侧, 继续在左右半区重复该操作, 直至整个数组有序

分区函数partition()的实现

挖坑法: 教材和校招的默认方法
取出数组第一个元素作为pivot, 此时该位置就空了. 从后往前, 找到第一个小于pivot的值,把它填到空的那个位置. 此时该位置就空了. 然后再从前往后找大于pivot的数, 填到空出来的位置. 一直循环, 直到左右指针重合, 把取出来的pivot放到该位置就完成了

代码

// 挖坑法快排
public static void quickSortHole(int[] arr) {
    quickSortHoleInternal(arr,0,arr.length - 1);
}

//在arr[l....r]进行快速排序
private static void quickSortHoleInternal(int[] arr, int l, int r) {
    // base case
    // 优化1.小数组使用插入排序
    //原本是if(r
    if (r - l <= 64) {
        insertionSort(arr,l,r);
        return;
    }
    int p = partitionByHole(arr,l,r);
    // 继续在两个子区间上进行快速排序
    quickSortHoleInternal(arr,l,p - 1);
    quickSortHoleInternal(arr,p + 1,r);
}

// 非递归的快排
public static void quickSortNonRecursion(int[] arr) {
    // 借助栈
    Deque<Integer> stack = new ArrayDeque<>();
    stack.push(arr.length - 1);
    stack.push(0);
    while (!stack.isEmpty()) {
        int l = stack.pop();
        int r = stack.pop();
        if (l >= r) {
            // 当前这个子数组已经处理完毕
            continue;
        }
        int p = partitionByHole(arr,l,r);
        // 先将右半区间压入栈中
        stack.push(r);
        stack.push(p + 1);
        // 继续处理左半区间
        stack.push(p - 1);
        stack.push(l);
    }
}
//分区函数
private static int partitionByHole(int[] arr, int l, int r) {
    // 优化2.每次分区选择随机数作为分区点 : 避免快排在近乎有序的数组上退化为O(n^2)的复杂度
    //原本是选择左侧的数据，但这样会导致在近乎有序的排序时，会退化为O(n)
    int randomIndex = random.nextInt(l,r);
    swap(arr,l,randomIndex);
    int pivot = arr[l];
    int i = l,j = r;
    while (i < j) {
        // 先让j从后向前扫描碰到第一个 < pivot的元素终止
        while (i < j && arr[j] >= pivot) {
            j --;
        }
        arr[i] = arr[j];
        // 再让i从前向后扫描碰到第一个 > pivot的元素终止
        while (i < j && arr[i] <= pivot) {
            i ++;
        }
        arr[j] = arr[i];
    }
    // 回填分区点
    arr[j] = pivot;
    return j;
}

补充

当数组近乎有序时, 快速排序会退化到O(n^2).
由于分区点元素每次取的都是最左侧元素, 若待排序集合近乎有序(极端情况下)完全有序. 则二叉树会变为单枝树, 高度变为N. 为了解决这个问题, 需要在分区点的选择上做改进

分区点的选择

①三数取中法(教材使用):
每次从无序数组中的最左侧,最右侧,中间位置取出其中中间大小的元素作为pivot
②随机数法:
每次从当前无序数组的随机位置作为分区点(上面代码写了)
③《算法4》的分区方法
选取第一个元素作为pivot(可以先用方法二选择pivot, 然后放到首位). 定义指针 l, j, i, r
其中l表示pivot, [l+1, j]是小于pivot的, [j+1, i-1]是大于pivot的, i是正在遍历的元素.
若当前元素小于pivot, 那么让j+1位置的元素与i位置元素交换, j++, i++
若当前元素大于pivot, 那么直接i++即可
当i==r遍历完毕. 完成后, 把l位置元素和j位置元素交换一下即可

④三路快排
当包含大量重复元素的时候使用.
l是pivot, [l+1, lt]是小于pivot, [lt+1, i-1]是等于pivot, [gt, r]是大于pivot
当i位置元素大于pivot, 交换i位置元素和gt-1位置元素, 然后gt–
当i位置元素小于pivot, 交换lt+1和i位置元素, lt++, i++
当i位置元素等于pivot, 直接i++

冒泡排序

堆排序

三. 外部排序

线性排序时间复杂度近乎O(n), 以下三种排序对于数据很敏感, 只能在特定场景下使用

桶排序

概念

将要排序的集合分散在若干个桶(子数组)中，子数组的内部排序好，整个数组就有序了

举例

现在要对陕西省所有高考考生进行排序. 假如有75个桶, 分别是[0,10), [10,20), [20,30), … [740,750]
把每个桶里的元素排好, 那么整个数组就有序了

计数排序

概念

计数排序其实是桶排序的特殊情况. 数据划分到不同的桶中后, 桶内元素都是相等元素, 内部不需要再排序, 只需要将原数组的所有元素扫描一遍之后, 划分到不同桶中即可.

举例

现在按照年龄把所有中国人排序, 有120个桶(0岁-120岁), 每扫描一个人就把他放进桶里, 扫描完了就排序好了

基数排序

概念

基数排序最明显的特征是可以按"位"排序. 若最高位已经大于另一个元素，其他位数不需要再次比较

举例

按照身份证号对所有人进行排序. 两个人开头第一位不一样, 后面就不需要比较了.