数据压缩实验三:用c语言实现Huffman编码和压缩效率分析
实验原理:
1.Huffman编码
Huffman编码是一种无失真的编码方式,是可变字长编码(VLC)的一种。
Huffman编码基于信源的概率统计模型,它的基本思路是:
出现概率大的信源符号编长码,出现概率小的信源符号编短码,从而使平均码长最小。
在程序实现时常使用一种叫树的数据结构实现Huffman编码,由它编出的码是即时码。
2.本实验中Huffman编码的算法
(1)将文件以ASCII字符流的形式读入,统计每个符号出现的频率;
(2)将所有文件中出现的字符按照频率从小到大的顺序排列;
(3)每一次选频率最小的两个值,作为二叉树的两个叶子节点,将和作为它们的父节点,这两个叶子节点不再参与比较,新的父节点参与比较;
(4)重复步骤(3),直到最后得到频率和为1的根结点;
(5)将形成的二叉树的左节点标0,右节点标1,把从最上面的根节点到最下面的叶子节点图中遇到的0、1序列串起来,得到各个字符的编码表示;
3.Huffman编码的数据结构表示
在程序实现中使用一种叫做二叉树的数据结构实现Huffman编码。
(1)Huffman节点结构
typedef struct huffman_node_tag
{
unsigned char isLeaf;//判断是否为树叶节点
unsigned long count;//节点表示的符号出现的次数
struct huffman_node_tag *parent;//该节点的父节点指针
union//共用体,该节点代表一个信源符号或者拥有左右子节点
{
struct
{
struct huffman_node_tag *zero, *one;//左右子节点指针,编码时左为0右为1
};
unsigned char symbol;//信源符号
};
} huffman_node;(2)Huffman编码的数据结构
typedef struct huffman_code_tag
{
unsigned long numbits;//码长(比特表示)
/* 码字,码字的第1位存于bits[0]的第1位 ,
码字的第2位存于bits[0]的第2位,
码字的第8位存于bits[0]的第8位,
码字的第9位存于bits[1]的第1位*/
unsigned char *bits;//指向该码字比特串的指针
} huffman_code;(3)Huffman编码的统计结果
typedef struct huffman_statistics_result
{
float freq[256];//每个信源符号出现频率
unsigned long numbits[256];//码长
unsigned char bits[256][100];//码字
}huffman_stat;Ps:上述三个结构体的创建均在下图(Huffman编码工程目录)的huffman.c文件中实现。

关键代码分析:
主函数(huffcode.c)中主要步骤分析:
/*step1: 创建和初始化文件读入、输出、表格文件输出指针及其他参数*/
main(int argc, char** argv)
{
char memory = 0;
char compress = 1;//编码为1解码为0
int opt;//将从命令行读取的数据赋值给opt
const char *file_in = NULL, *file_out = NULL;//输入输出文件指针
//step1:add by yzhang for huffman statistics
const char *file_out_table = NULL;//表格文件
//end by yzhang
FILE *in = stdin;//定义指向输入缓冲区的文件指针
FILE *out = stdout;//定义指向输出缓冲区的文件指针
//step1:add by yzhang for huffman statistics
FILE * outTable = NULL;//输出统计数据文件
//end by yzhang/* step2:调用getopt函数获取和解析命令行参数 */
while((opt = getopt(argc, argv, "i:o:cdhvmt:")) != -1) //演示如何跳出循环,及查找括号对;当读取非空
{
switch(opt)
{
case 'i':
file_in = optarg;//optarg指向i额外的参数
break;
case 'o':
file_out = optarg;
break;
case 'c':
compress = 1;//设置为编码
break;
case 'd':
compress = 0;//设置为解码
break;
case 'h':
usage(stdout);//帮助显示使用方法
return 0;
case 'v':
version(stdout);//输出版本信息
return 0;
case 'm':
memory = 1;//改变内存中的值
break;
// by yzhang for huffman statistics
case 't'://输出数据统计文件
file_out_table = optarg;
break;
//end by yzhang
default:
usage(stderr);//如果是其他情况,则将使用方法信息送到标准错误文件
return 1;
}
}
/* step3:打开输入输出文件 */
if(file_in)
{
in = fopen(file_in, "rb");
if(!in)
{
fprintf(stderr,
"Can't open input file '%s': %s\n",
file_in, strerror(errno));
return 1;
}
}
if(file_out)
{
out = fopen(file_out, "wb");
if(!out)
{
fprintf(stderr,
"Can't open output file '%s': %s\n",
file_out, strerror(errno));
return 1;
}
}
//by yzhang for huffman statistics
if(file_out_table)
{
outTable = fopen(file_out_table, "w");/*以写的方式打开一个文件,并赋值给文件指针outTable*/
if(!outTable)
{
fprintf(stderr,
"Can't open output file '%s': %s\n",
file_out_table, strerror(errno));
return 1;
}
}
//end by yzhang/*step4:关键部分!Huffman编码部分*/
if(compress) //change by yzhang 如果是编码,输入文件,编码再输出文件的同时,输出统计数据
huffman_encode_file(in,out,outTable);//step1:changed by yzhang from huffman_encode_file(in, out) to huffman_encode_file(in, out,outTable)
else
huffman_decode_file(in, out);//否则只进行解码/*step5:收尾工作:关闭文件*/
if(in)//如果指向输入文件的这块内存还存在,关闭
fclose(in);
if(out)
fclose(out);//关闭
if(outTable)
fclose(outTable);//关闭
return 0;
}子函数文件(huffman.c)中的编码步骤分析:
第一次扫描,统计文件中各个字符出现频率:(8bit,共256个符号)
1.创建一个256个元素的指针数组,用来保存256个信源符号的频率,其下标对应相应字符的ASCII码值。
2.数组中的非空元素为当前待编码文件中实际出现的信源符号。
/*保存频率的指针数组*/
typedef huffman_node* SymbolFrequencies[MAX_SYMBOLS];//MAX_SYMBOLS=256
SymbolFrequencies sf;/*获得各符号频数*/
static unsigned int get_symbol_frequencies(SymbolFrequencies *pSF, FILE *in)
{
int c;
unsigned int total_count = 0;//用于计算符号出现次数
init_frequencies(pSF);//初始化这些符号的频率全部为0
/*第一次扫描*/
while((c = fgetc(in)) != EOF)//从文件中读取一字节字符,并赋值给c
{
unsigned char uc = c;//重置为字符
/*新建了一个节点.。uc又指字符,又指频率数组的第uc个值,这样可以满足排序问题; 如果uc的结构体不存在,则新建*/
if(!(*pSF)[uc])
(*pSF)[uc] = new_leaf_node(uc);
++(*pSF)[uc]->count;//读了一个uc,个数加1
++total_count;//总个数加1
}
return total_count;
}/*获得各符号频率:统计频率,并赋值给统计数据结构体的频率变量*/
int huffST_getSymFrequencies(SymbolFrequencies *SF, huffman_stat *st,int total_count)
{
int i,count =0;
for(i = 0; i < MAX_SYMBOLS; ++i)
{
if((*SF)[i])//如果i符号存在
{
st->freq[i]=(float)(*SF)[i]->count/total_count;//这个符号的频率设置为符号个数除以总频率
count+=(*SF)[i]->count;
}
else
{
st->freq[i]= 0;//不存在则频率为0
}
}
if(count==total_count)
return 1;
else
return 0;
}建立Huffman树,并计算符号对应的Huffman码字
1.按频率从小到大进行排序并建立Huffman树
static SymbolEncoder*
calculate_huffman_codes(SymbolFrequencies * pSF)//返回为编码结构体指针
{
unsigned int i = 0;
unsigned int n = 0;
huffman_node *m1 = NULL, *m2 = NULL;//定义两个节点指针,置为空
SymbolEncoder *pSE = NULL;//定义一个编码指针为空
#if 1
printf("BEFORE SORT\n");
print_freqs(pSF); //演示堆栈的使用,打印符号和出现次数
#endif/*1对256个节点进行排序*/
qsort((*pSF), MAX_SYMBOLS, sizeof((*pSF)[0]), SFComp); //qsort为排序函数,按频率从小到大排。排序顺序由SFcomp函数给出,该函数在后面给出其具体实现
#if 1
printf("AFTER SORT\n");
print_freqs(pSF);//再次显示符号和次数(排序后)
#endif
for(n = 0; n < MAX_SYMBOLS && (*pSF)[n]; ++n)//节点存在且小于256时,即获得频率为非零节点的个数/*2对排好序的节点计算码字*/
for(i = 0; i < n - 1; ++i)
{
//处理频率最小的两个节点
m1 = (*pSF)[0];
m2 = (*pSF)[1];
(*pSF)[0] = m1->parent = m2->parent =
new_nonleaf_node(m1->count + m2->count, m1, m2);//创建这两个最小频率节点的父节点,并将其的父节点赋值,全部赋给第左节点,右节点赋为空
(*pSF)[1] = NULL;
qsort((*pSF), n, sizeof((*pSF)[0]), SFComp);//再次进行排序
}/* 3由建立的huffman树对每个符号生成码字 */
pSE = (SymbolEncoder*)malloc(sizeof(SymbolEncoder));
memset(pSE, 0, sizeof(SymbolEncoder));
build_symbol_encoder((*pSF)[0], pSE);
return pSE;
}
/*遍历整个树,对存在的码字计算码字*/
static void
build_symbol_encoder(huffman_node *subtree, SymbolEncoder *pSF)//对符号进行编码,前一个是指树,后一个是指编码结构体指针
{
if(subtree == NULL)//树为空,不编码
return;
if(subtree->isLeaf)//如果为树叶节点,则进行编码
(*pSF)[subtree->symbol] = new_code(subtree);//编码函数
else//不是树叶节点的话
{
build_symbol_encoder(subtree->zero, pSF);//先对其左子节点编码
build_symbol_encoder(subtree->one, pSF);
}
}/*new_code函数*/
static huffman_code*
new_code(const huffman_node* leaf)//为该节点编码
{
/* Build the huffman code by walking up to
* the root node and then reversing the bits,
* since the Huffman code is calculated by
* walking down the tree. */
unsigned long numbits = 0;//码长初始化为0
unsigned char* bits = NULL;//指向码字的指针
huffman_code *p;//
while(leaf && leaf->parent)//当叶子节点存在且其父节点存在时:父节点存在说明该码还没有编完,继续编
{
huffman_node *parent = leaf->parent;//父指针指向父节点
unsigned char cur_bit = (unsigned char)(numbits % 8);//因为一字节8比特,用cur_bit判断是否凑足一字节
unsigned long cur_byte = numbits / 8;
if(cur_bit == 0)//当凑足一字节
{
size_t newSize = cur_byte + 1;//再多分配一字节
bits = (char*)realloc(bits, newSize);/*注意realloc函数与malloc不同,它在保持原有数据不变的情况下重新分配新的空间,原有数据保存在新 空间的的前面部分(空间的地址可能有变化)*/
bits[newSize - 1] = 0;//且将多分配的字节初始化为0
}
if(leaf == parent->one)//如果该节点是其父节点的右子节点,则,左子节点不处理,因为初始化为0,右子节点赋为1
bits[cur_byte] |= 1 << cur_bit;//左移到当前比特的当前位,继续编码
++numbits;//编了一位码,码长+1
leaf = parent;//将其父节点赋给当前节点,再循环
}
if(bits)//编完码,且码字存在,按照Huffman编码规则,码字需要翻转
reverse_bits(bits, numbits);
p = (huffman_code*)malloc(sizeof(huffman_code));
p->numbits = numbits;
p->bits = bits;
return p;
}/*reverse_bits函数的具体实现*/
static void reverse_bits(unsigned char* bits, unsigned long numbits)//码字翻转
{
unsigned long numbytes = numbytes_from_numbits(numbits);//获得该码字所占字节数
unsigned char *tmp =(unsigned char*)alloca(numbytes);//alloca是内存分配函数,在栈上申请空间,用完立即释放,用于存放翻转后的码字
unsigned long curbit;//对码字进行未操作
long curbyte = 0;//对码字进行字节操作
memset(tmp, 0, numbytes);//将tmp中的前numbytes个字节全部换成0
for(curbit = 0; curbit < numbits; ++curbit)//当前的比特
{
unsigned int bitpos = curbit % 8;//定位当前位在一个字节的第几位
if(curbit > 0 && curbit % 8 == 0)//当超过一字节,将当前字节定位到下一字节
++curbyte;
tmp[curbyte] |= (get_bit(bits, numbits - curbit - 1) << bitpos);/*依次获取相应bit位并将其移到逆序后对应位置,再与前一bit位逆序后所得字节或运算,得到逆序后码字:如curbit为0,则对应与最高位交换,get_bit获取最高位后返回0000000i,i为最高位的码,再与00000000或之后返回给tmp.*/
}
memcpy(bits, tmp, numbytes);//从tmp中拷贝numbytes个字节到bits中
}
/*numbytes_from_numbits函数的实现*/
static unsigned long numbytes_from_numbits(unsigned long numbits)//比特转字节函数
{
return numbits / 8 + (numbits % 8 ? 1 : 0);//一字节八比特,返回为字节,上取整的方法
}
/*SFComp函数的具体实现*/
static int
SFComp(const void *p1, const void *p2)//是一个确定排序顺序的比较函数,按频率来排序
{
const huffman_node *hn1 = *(const huffman_node**)p1;//字符指针强制转换为结构体指针
const huffman_node *hn2 = *(const huffman_node**)p2;
/* Sort all NULLs to the end. */
if(hn1 == NULL && hn2 == NULL)//两节点都为空,返回0
return 0;//前=后
if(hn1 == NULL)
return 1;//hn1放在hn2后
if(hn2 == NULL)
return -1;//hn1放在hn2前
if(hn1->count > hn2->count)
return 1;//hn1放在hn2后
else if(hn1->count < hn2->count)
return -1;//hn1放在hn2前
return 0;
}/*get_bit函数的实现*/
static unsigned char get_bit(unsigned char* bits, unsigned long i)//写比特
{
return (bits[i / 8] >> i % 8) & 1;//获取第i位,如获取码字101010001的第7位“0”,则返回0000 0000和1的与
}/*new_nonleaf_node函数的具体实现*/
static huffman_node*
new_nonleaf_node(unsigned long count, huffman_node *zero, huffman_node *one)//非叶子节点的结构体创建
{
huffman_node *p = (huffman_node*)malloc(sizeof(huffman_node));//为该节点创建一块内存区
p->isLeaf = 0;//非叶子节点
p->count = count;//总数是其子节点之和
p->zero = zero;//左节点指针
p->one = one;//右节点指针
p->parent = 0;//没有父节点 ----ps:都是通过节点连接其子节点来说明节点间的相互关系
return p;
}将每个符号的码长和码字赋给编码结果统计数据结构体:
int huffST_getcodeword(SymbolEncoder *se, huffman_stat *st)
{
unsigned long i,j;
for(i = 0; i < MAX_SYMBOLS; ++i)
{
huffman_code *p = (*se)[i];
if(p)//编码结构体存在时
{
unsigned int numbytes;
st->numbits[i] = p->numbits;//将编完码的码长赋给统计数据结构体
numbytes = numbytes_from_numbits(p->numbits);
for (j=0;jbits[i][j] = p->bits[j];//将编完码的码字赋给统计数据结构体
}
else
st->numbits[i] =0;//不存在则该符号出现频率为0,没有进行编码
}
return 0;
} 将Huffman码表写入文件
for(i = 0; i < MAX_SYMBOLS; ++i)
{
huffman_code *p = (*se)[i];
if(p)
{
unsigned int numbytes;
fputc((unsigned char)i, out);//将信源符号写进输出文件
fputc(p->numbits, out);//将信源符号对应的码长写入文件
numbytes = numbytes_from_numbits(p->numbits);//将信源符号编成的码字写入文件
if(fwrite(p->bits, 1, numbytes, out) != numbytes)
return 1;
}
}将统计数据写入输出统计文件
void output_huffman_statistics(huffman_stat *st,FILE *out_Table)
{
int i,j;
unsigned char c;
fprintf(out_Table,"symbol\t freq\t codelength\t code\n");//输出文件表头
for(i = 0; i < MAX_SYMBOLS; ++i)
{
fprintf(out_Table,"%d\t ",i);//输出信源符号
fprintf(out_Table,"%f\t ",st->freq[i]);//输出信源符号的频率
fprintf(out_Table,"%d\t ",st->numbits[i]);//输出信源符号编码后的码长
if(st->numbits[i])//如果码长大于1,即进行了编码
{
for(j = 0; j < st->numbits[i]; ++j)
{
c =get_bit(st->bits[i], j);
fprintf(out_Table,"%d",c);//输出信源符号编码后的码字
}
}
fprintf(out_Table,"\n");
}
}第二次扫描文件,对文件查表进行huffman编码,并写入输出文件
static int
do_file_encode(FILE* in, FILE* out, SymbolEncoder *se)
{
unsigned char curbyte = 0;
unsigned char curbit = 0;
int c;
while((c = fgetc(in)) != EOF)//遍历文件
{
unsigned char uc = (unsigned char)c;
huffman_code *code = (*se)[uc];//查表
unsigned long i;
for(i = 0; i < code->numbits; ++i)//将码字写入文件
{
/* */
curbyte |= get_bit(code->bits, i) << curbit;//写入当前字节的每一位
if(++curbit == 8)//当凑足一个字节,则将这一字节写入文件,将当前bit和byte都置零,重新写入一个字节
{
fputc(curbyte, out);
curbyte = 0;
curbit = 0;
}
}
}
//若多出不够凑出一字节,则作为一字节输出
if(curbit > 0)
fputc(curbyte, out);
return 0;
}实验结果分析:
| 文件类型 |
平均码长 |
信源熵 |
原文件大小(kb) |
压缩后文件大小(kb) |
压缩比 |
| ppt |
6.337851 |
6.309532 |
182 |
146 |
1.247 |
| |
7.630489 |
7.587450 |
300 |
287 |
1.045 |
| png |
7.999920 |
7.997800 |
328 |
329 |
0.996 |
| bmp |
7.835411 |
7.799278 |
554 |
544 |
1.018 |
| docx |
7.999294 |
7.995741 |
264 |
265 |
0.996 |
| jpg |
7.868257 |
7.842246 |
1062 |
1045 |
1.016 |
| html |
5.015010 |
6.260903 |
31 |
25 |
1.240 |
| txt |
5.896542 |
5.866860 |
1 |
1 |
1.000 |
| rar |
7.999984 |
7.998295 |
4386 |
4386 |
1.000 |
| gif |
7.939629 |
7.909703 |
59 |
58 |
1.017 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
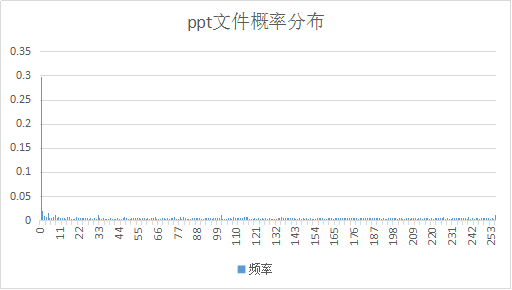
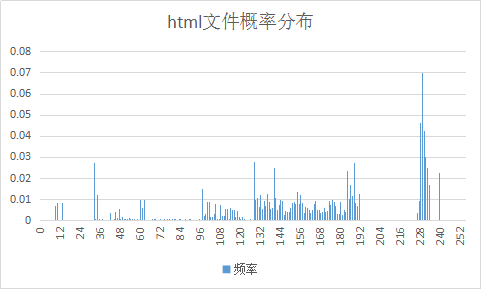
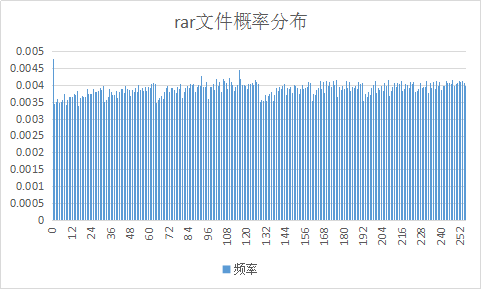
分析上表和上图:可知Huffman编码对于不同格式的文件,其压缩效率不同。具体来说,当概率较集中在某几个符号时,用Huffman编码可以得到较大压缩比(如上面的ppt、pdf、html文件),而当符号分布较均匀时,则得到较小压缩比甚至压缩比<1(如png和docx,这两个文件概率分布较均匀,码表所占的内存大导致压缩比甚至小于1,其他接近于1的文件也主要是因为符号分布较均匀而不能用较少的码字来编码导致压缩效率不高)
实验结论:
1、Huffman编码算法是一种无失真编码,虽然在编码原理较为容易,但在工程应用上应用不多,因为该编码方法适用于信源符号单一且集中分布的文件,而实际工程应用上的文件却是十分复杂的。这会导致其传输的码表占据很大内存,从而降低压缩效率。
2、该程序实现的过程用到了二叉树这种数据结构。展开来讲,对于一种数据结构的分析,应该从其逻辑结构和存储结构两方面分析。逻辑结构即其内部元素之间的相关性;存储结构即其元素存储位置的相关性。


