机器学习:sklearn中的线性回归
线性模型
一:线性模型的概念:
在回归分析当中,线性模型的一般预测公式如下:![]()
式中:x[0],x[1],…,x[p]为数据集中特征变量的数量(这个公式表示数据集中的数据点一共有p个特征);w和b为模型的参数;y为模型对于数据结果的预测值。对于只有一个特征变量的数据集,公式可以简化为:
y=w[0]乘以x[0]+b
| 线性回归的基本原理 |
|---|
| 找到当训练数据集之中y的预测值和其真实值的平方差最小的时候,所对应的w值和b值。 |
二:最基本的线性模型:
线性回归,也成为普通最小二乘法,是在回归分析中最简单也是最经典的线性模型。
使用make_regression函数,生成样本数量为100,特征数量为2的数据集。并且用train_test_split函数将数据集分割成训练数据集和测试数据集。
代码如下:
#coding=gbk;
import numpy as np;
import matplotlib.pyplot as plt;
#生成用于回归分析的数据集
from sklearn.datasets import make_regression;
#导入线性回归模型:
from sklearn.linear_model import LinearRegression;
#--------------------------------------------------------------
#生成用于回归分析的数据集:
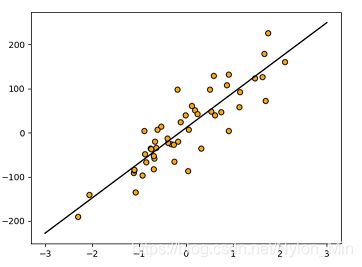
X,y=make_regression(n_samples=50,n_features=1,n_informative=1,\
noise=50,random_state=1);
reg=LinearRegression()
reg.fit(X,y);
#--------------------------------------------------------------
#z是我们生成的等差数列,用来画出线性模型的图形。
z=np.linspace(-3,3,200).reshape(-1,1);
plt.scatter(X,y,c="orange",edgecolors='k');
plt.plot(z,reg.predict(z),c="k");
plt.show()
#--------------------------------------------------------------
print("直线的系数为:{}".format(reg.coef_))
print("直线的截距为:{}".format(reg.intercept_))
最基本线性回归模型小结:
- 在使用这种最基本的线性回归的时候,有可能遇到两种不好的情况:1、欠拟合;2、过拟合。
一般来说,欠拟合有可能因为:特征量过少;
过拟合有可能是因为:特征量太多而数据太少;
三: 使用L2正则化的线性模型——岭回归
从实用的角度来说,岭回归实际上是一种能够避免过拟合的线性模型。在岭回归中,模型会保留所有的特征变量,但是会减小特征变量的系数值,让特征变量对预测结果的影响变小,在岭回归中实际上是通过改变其alpha参数来控制减小特征变量系数的程度。
结合吴恩达先生的机器学习的某一些讲解,其实可以理解成就是加了一个惩罚项,而上面所说的alpha就相当于是惩罚项的系数。alpha越大,那么“惩罚”的程度就越重,所以特征的系数就会越小。反之,alpha越小,那么特征的系数就会相应的增大。
默认的时候,alpha为1.
代码如下:
#coding=gbk
import numpy as np;
import matplotlib.pyplot as plt;
#载入数据集
from sklearn.datasets import load_diabetes;
#数据拆分工具
from sklearn.model_selection import train_test_split;
#导入岭回归:
from sklearn.linear_model import Ridge;
#--------------------------------------------------------------
#先载入数据集
X,y=load_diabetes().data,load_diabetes().target;
#将数据集拆分成训练集和测试集
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=8);
#--------------------------------------------------------------
print("************************************")
print("X_train的大小为:{t}".format(t=X_train.shape))
print("y_train的大小为:{t}".format(t=y_train.shape))
print("X_test的大小为:{t}".format(t=X_test.shape))
print("y_test的大小为:{t}".format(t=y_test.shape))
print("************************************")
#--------------------------------------------------------------
ridge=Ridge();
ridge.fit(X_train,y_train);
print("训练集的得分为:{:.2f}".format(ridge.score(X_train,y_train)));
print("测试集的得分为:{:.2f}".format(ridge.score(X_test,y_test)));
运行结果如下:
这时是默认的alpha,为1

现在将alpha设置为10
ridge=Ridge(alpha=10);
ridge.fit(X_train,y_train);
运行结果为: 可以看到,得分都下降了。alpha过大,其实也会欠拟合。
可以看到,得分都下降了。alpha过大,其实也会欠拟合。
现在将alpha设置为0.01
ridge=Ridge(alpha=0.1);
ridge.fit(X_train,y_train);
岭回归小结:
- 当训练集没有那么大的时候,正则化会显得比较重要。但是当训练集很大的时候,正则化就显得不那么重要了。因为这个时候训练集很大,即便是最基本的线性回归模型,也基本上不会出现过拟合。
四:使用L1正则化的线性模型——套索回归
和岭回归一样,套索回归也会将系数限制在非常接近于0的范围内,但是它进行限制的方式有一点不同。与L2正则化不同的是,L1正则化会导致使用套索回归的时候,有一部分特征的系数会正好等于0.也就是说,有一些特征会彻底被模型忽略掉。
对于套索回归,也是通过改变alpha的值,来决定正则化的程度。默认时alpha=1;
代码如下:
#coding=gbk
import numpy as np;
import matplotlib.pyplot as plt;
#载入数据集
from sklearn.datasets import load_diabetes;
#数据拆分工具
from sklearn.model_selection import train_test_split;
#导入套索回归:
from sklearn.linear_model import Lasso;
#先载入数据集
X,y=load_diabetes().data,load_diabetes().target;
#将数据集拆分成训练集和测试集
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=8);
lasso=Lasso()
lasso.fit(X_train,y_train);
print("训练集的得分为:{:.2f}".format(lasso.score(X_train,y_train)));
print("测试集的得分为:{:.2f}".format(lasso.score(X_test,y_test)));
print("套索回归使用到的特征数:{}".format(np.sum(lasso.coef_!=0)))
套索回归小结:
- 降低alpha值可以拟合出更复杂的模型,从而在训练数据集和测试数据集都能获得良好的表现。相对岭回归,套索回归的表现还要稍好一点,而且它只用了10个特征中的7个
但是,如果我们把alpha值设置得太低,就等于把正则化的效果去除了,那么模型就可能会像线性回归一样,出现过拟合的问题。
五:线性回归总结:
- 在线性回归,岭回归和套索回归中,是通过alpha参数来进行调节的。
- 在实际应用中,我们需要决定是使用L1正则化模型还是L2正则化模型。
一般来说,如果数据集由很多特征,而这些特征并不是每一个都对结果由重要的影响,那么就应该使用L1正则化模型,即套索回归;但是如果数据集的特征本来就不多,而且每一个都很重要,那么就应该用L2正则化的模型,如岭回归。
遇事不决,可问春风。