羊羊刷题笔记Day01/60 | 第一章 数组P1 | 704. 二分查找、27. 移除元素

学习资料：本专栏学习路线来自代码随想录算法训练营
数组基础理论
704 二分查找
27 移除元素

数组基础理论

关于数组存储问题——不同编程语言的内存管理是不一样

结论：不同的语言，数组的存储情况不同

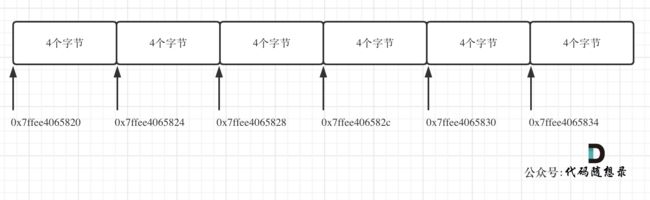
以C++为例，在C++中二维数组是连续分布的。
我们来做一个实验，C++测试代码如下：

void test_arr() {
    int array[2][3] = {
		{0, 1, 2},
		{3, 4, 5}
    };
    cout << &array[0][0] << " " << &array[0][1] << " " << &array[0][2] << endl;
    cout << &array[1][0] << " " << &array[1][1] << " " << &array[1][2] << endl;
}

int main() {
    test_arr();
}

测试地址为

0x7ffee4065820 0x7ffee4065824 0x7ffee4065828
0x7ffee406582c 0x7ffee4065830 0x7ffee4065834
//地址为16进制，c为12

如图：

所以在C++中二维数组在地址空间上是连续的。

Java：
像是没有指针的，同时也不对程序员暴露其元素的地址，寻址操作完全交给虚拟机。
所以看不到每个元素的地址情况，这里我以Java为例，也做一个实验。

zpublic static void test_arr() {
    int[][] arr = {{1, 2, 3}, {3, 4, 5}, {6, 7, 8}, {9,9,9}};
    System.out.println(arr[0]);
    System.out.println(arr[1]);
    System.out.println(arr[2]);
    System.out.println(arr[3]);
}

输出的地址为：

[I@7852e922
[I@4e25154f
[I@70dea4e
[I@5c647e05

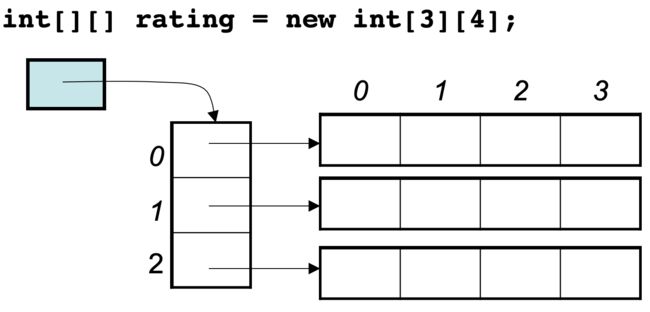
这里的数值也是16进制，这不是真正的地址，而是经过处理过后的数值了，我们也可以看出，二维数组的每一行头结点的地址是没有规则的，更谈不上连续。
所以Java的二维数组可能是如下排列的方式：

704 二分查找

上手练习：

第一次错误

第二次错误：

第三次错误：晕了

最终代码：

public int search(int[] nums, int target) {
    int start = 0;
    int end = nums.length;
    int middle = (start + end) / 2;

    if (nums.length == 1) {
        if (nums[0] == target) {
            return 0;
        }else return -1;
    }

    while (start <= end) {
        if (nums[middle] > target) {
            end = middle;
            middle = (start + end) / 2;
        } else if (nums[middle] < target) {
            start = middle;
            middle = (start + end) / 2;
        } else if (nums[middle] == target) {
            return middle;
        } else if (middle == start && start == end) {
            if (nums[middle] == target){
                return middle;
            }else return -1;
        }
    }
    return -1;
}

看视频：

易错点：

• while (start < end) or (start <= end)?
• start = middle or middle - 1?

“把握不好出现小问题，虽然说是小问题，但运行不起来就是大问题”

原理：
根源在于：没弄清楚区间定义 左闭右闭[ ] or 左闭右开[ )

• 为什么要进行区间定义（ 左闭右闭[ ] or 左闭右开[ ) ）：

涉及到易错点中，到底是< or <=? middle or middle - 1

• 为什么会突然想到“< or <=? middle or middle - 1”问题：

分别对应实际写代码时遇到：循环结束的条件是什么？start 和 end 下一步要去到哪？
因此，需要一个标准去衡量

左闭右闭：
(start < end) or (start <= end)问题：[1,1]
由于两边闭合，start <= end位于合法区间
middle or middle - 1问题:
由于两边闭合，在条件判断中已经确定下标middle的大小
因此下一次的边界在middle - 1 or middle + 1;

左闭右开：与上同理
(start < end) or (start <= end)问题：[1,1)
由于左闭右开，start < end位于合法区间 (此时start = end不符合定义)
middle or middle - 1问题:
由于左闭右开（不包含右值），在条件判断中已经确定下标middle的大小
因此下一次的边界在middle or middle;

卡哥：
二分法是非常重要的基础算法，为什么很多同学对于二分法都是一看就会，一写就废？
其实主要就是对区间的定义没有理解清楚，在循环中没有始终坚持根据查找区间的定义来做边界处理。
区间的定义就是不变量，那么在循环中坚持根据查找区间的定义来做边界处理，就是循环不变量规则。
本篇根据两种常见的区间定义，给出了两种二分法的写法，每一个边界为什么这么处理，都根据区间的定义做了详细介绍。

个人感觉，左闭右闭写法会更不易绕进去，毕竟左闭右开的右区间还存在不包含，意味着已经自动-1 or +1

27 移除元素

运用之前学习过数据结构记忆的知识，删除一个集体往前移的传统方法，当时用C实现，现在用Java实现：

int length = nums.length;
// 1.逐个扫描并删除
for (int i = 0; i < length; i++) {
    if (nums[i] == val){
        // 2.前移
        for (int i1 = i; i1 < length - 1; i1++) {
            nums[i1] = nums[i1 + 1];
        }
        i--;
        length--;
    }
}
return length;

解答成功:
执行耗时:0 ms,击败了100.00% 的Java用户
内存消耗:39.7 MB,击败了96.77% 的Java用户

双指针法：

// 双指针法
int low = 0;

for (int fast = 0; fast < nums.length; fast++) {// fast指针探路
    // fast所指数值不是val 交换值 并继续探路
    if (nums[fast] != val){
        nums[low] = nums[fast];
        low++;
    }
    // 否则low指向特定值val，fast继续探路
}

return low;

解答成功:
执行耗时:0 ms,击败了100.00% 的Java用户
内存消耗:39.7 MB,击败了97.04% 的Java用户

虽然这个之前也学过，但今天写后有更深的理解：
fast 为探路者，寻找宝藏（不是val） low是收拾后场，用宝藏把废物换掉

• fast指针只要找到宝就往前面丢
• low指针到fast都是垃圾，那么结束后自然low为整个数组的长度