数字图像处理笔记（二）图像增强-直方图修改技术

前言：本篇笔记，在于了解图像增强的直方图修改技术有哪些方法以及设计到的数学原理。
参考：阮秋琦 第3版《数字图像处理学》、黄琳琳 图像处理与机器学习视频
感想：用到了很多概率论和高等数学的知识。

图像增强介绍

为什么需要图像增强？：图像有时候会出现视觉效果不佳、噪声污染、难以分析等问题。

图像增强：用来突出图像中感兴趣的信息，而减弱或者去除不必要的信息，使其更便于人眼观察或者机器分析。

图像增强的方法：空域法（点处理、邻域处理）、频域法。
直方图修改技术和灰度变换都属于空域法的点处理。

灰度变换

灰度变换：输入图像像素的灰度级进行变换。
$$s=T(r)(r输入灰度级，s输出灰度级，T灰度变换函数)$$

灰度变换函数：

• 线性变换（s=Ar+B）：有分段和不分段，分段线性变换，对感兴趣部分灰度拉伸，对不感兴趣的部分灰度压缩。
• 非线性变换：对数变换、幂次变换、直方图均衡等。

直方图

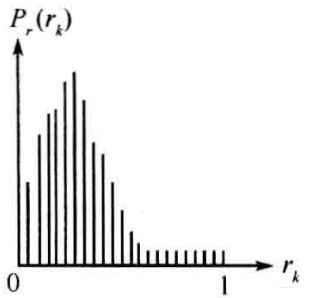
灰度级的直方图，反应一幅图像中灰度级和出现这种灰度级概率之间的关系。

像素的灰度级用变量r来表示，可以归一化处理：0<=r<=1。
r=0表示黑，r=1表示白。

用概率密度函数p_r( r )表示灰度分布。

为利于数字图像处理，引入离散形式，用r_k表示离散灰度级，并用P_r( r )代替p_r( r )。
$$P_r(r_k)=\frac{n_k}{n}(0\le r_k\le 1)k=0,1,2,...,l-1$$
上图中，n_k表示为r_k灰度级出现的像素个数，n为总像素个数。

直方图修改技术的基础

直方图修改实际上是对r值做变换：s=T( r )。

变换函数T( r )的要求：

• 在0<=r<=1区间内，T( r )单调递增。保证图像灰度级从白到黑的次序不变。
• 对于0<=r<=1，都有0<=T( r )<=1。保证映射之后的像素灰度不超过范围。

主要搞清楚灰度变换前后的直方图有什么关系？：变换只是针对像素上的灰度级进行变换，变换前和变换后的部分像素个数还是相等的，例如对区间[0.5,0.9]灰度级r进行变换函数到[0.1,0.3]灰度级s上，这两个灰度级区间所拥有的像素个数是不变的。其实就是概率论里面的随机变量函数的分布的特点。
$$P(\mu \le s)=P[\xi \le r]={\int }_{-\infty }^r{p}_r(x)\mathrm{dx}$$
通过分布函数求导可以求出概率密度函数。
$$p_s(s)=p_r(r)\times \frac{dr}{ds}(r=T^{-1}(s))$$

直方图均衡化处理（直方图线性化处理）

为什么需要直方图均衡化处理？：从直方图可以看出像素的灰度级分布，如果大多数像素集中在较暗的区域，会使得图像看起来过暗；反过来，如果大多数像素集中在较亮的区域，会使得图像看起来过亮。可以通过直方图均匀化，让每个灰度级上分布的像素更加均匀，使得图像的细节看起来更加丰富。

接下来会进行直方图均衡化处理的变换函数的推导。

直方图均衡化之后，应该是一个均匀分布，在区间[0,1]上服从均匀分布的概率密度取值为1（1/区间长度）。
$$p_s(s)=p_r(r)\times \frac{dr}{ds}=1$$
可以得出
$$\frac{dr}{ds}=\frac{1}{\frac{ds}{dr}}=\frac{1}{p_r(r)}$$
$$\frac{ds}{dr}=p_r(r)$$
也就意味着
$$s=T(r)={\int }_0^r{p}_r(x)\mathrm{dx}$$
这样一旦知道了p_r函数，就可以通过变上限积分求解出T( r )。

以上都是基于连续性随机变量进行讨论的，但对于数字图像，需要引入离散形式的公式。
$$s_k=T(r_k)=\sum _{j=0}^k\frac{n_j}{n}=\sum _{j=0}^k{P}_r(r_j)$$
需要掌握r_k通过离散形式变换得到s_k的过程，从而理解到直方图均衡化的缺陷。
直方图均衡化处理步骤：
1）先求出不同r_k对应的P_r( r_k )（P_r计算在前面直方图部分就有）。
2）通过累积分布函数（上述公式）做变换得到s_k。
3）得到的s_k需要选择最靠近的一个灰度级，作为新的灰度级。例如s_k=0.19，原先的灰度级有0、1/3、2/3、1，这时候最近的灰度级是1/3。

直方图均衡化的缺陷：简并现象。
简并现象：第三步用新灰度级替代旧灰度级的时候，会导致变换后灰度等级总数减少。简并会导致出现伪轮廓(False Contour)，画面本该平坦的区域出现了类似于等高线一样不连续的过渡带。
原因：累积分布函数得到s_k往往是不允许的灰度值，用最接近的灰度来替代它时，一些相邻的s_k会变成相同灰度级。
如何减少：
1）增加像素的比特数，也就是增加像素深度，让能表示的灰度层级更多，来减少多个相邻的s_k并入到同一个深度级。
2）灰度间隔放大理论（保留疑问，书上看的不是很懂，等理解后再补充？？？）。

直方图规定化处理

直方图规定化处理：修改一幅图像直方图，使得它接近和规定结果图像的直方图。

其中原始图像的概率密度函数是P_r( r )，而希望得到的图像概率密度函数是P_z( z )。

关键在于如何建立P_r( r )和P_z( z )之间的联系。
1）对两幅图像都进行直方图均衡化。
$$s=T(r)={\int }_0^r{p}_r(x)\mathrm{dx}v=G(z)={\int }_0^z{p}_z(x)\mathrm{dx}$$
2)两幅图像只是灰度分布概率密度不同，但是像素个数是相同的。由于两幅图像都做了均衡化处理，所以当s=v时
$$s=v={\int }_0^r{p}_r(x)\mathrm{dx}={\int }_0^z{p}_z(x)\mathrm{dx}$$
则推出
$${\int }_s^{s+\Delta s}1\mathrm{dx}={\int }_r^{r+\Delta r}{p}_r(x)\mathrm{dx}={\int }_z^{z+\Delta z}{p}_z(x)\mathrm{dx}$$
就是在$\Delta s,\Delta r,\Delta z$这段灰度区间像素个数相等，也就是像素个数没变灰度变了。
3）这个时候就可以得出r和z的映射关系了，
$$z=G^{-1}(v)=G^{-1}(s)=G^{-1}[T(r)]$$
也就是$z=G^{-1}[T(r)]$。

如何处理映射关系中的反函数？
虽然映射关系中要求反函数的解析式，这个在连续随机变量中是很困难的，但是由于数字图像处理是离散变量，所以可以用近似来绕过。
也就是可以通过$v=G(z),s=T(r)$求出不同v和s配对的z和r，然后通过判断$v\approx s$来吧配对的z和r关联起来就好了。

图像对比度处理

利用灰度变换和直方图修正可以对图像对比度进行处理。直方图均衡化处理可以改善图像灰度的动态范围；直方图规定化可以得到更加符合需求的结果；正确的灰度变换函数设计可以灵活改善图像。

几种常用的对比度处理的灰度变换函数：
1）对比度增强：线性递增的灰度变换函数，把输入灰度区间映射到整个灰度输出范围。

2）灰度反转：线性递减的灰度变换函数。

3）开窗式/灰度窗口变换：将某一个区间的灰度级和其它部分区分开来。

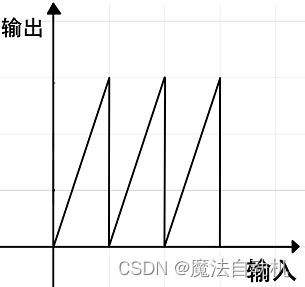
4）锯齿形变换：通过把几段较窄的输入灰度区间映射到整个灰度输出范围，把变换较为平缓的部分更清晰的显示出来。