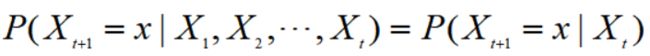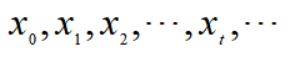MCMC（马尔可夫链）

1.马尔可夫链由状态空间和转移矩阵定义

2.齐次马尔可夫链是指未来状态的条件概率分布仅依赖于现在状态，与过去无关

3.如果马氏链的每个状态都会趋于一个稳定的数值，我们称过程收敛

4.如果分布π(X)使得停留在某一状态的概率与从随机采样的前期状态转移到它的概率相同，该马氏链称为平稳分布

5.平稳分布就是表示在某一个时刻后，分布不再改变

6.细致平衡是平稳分布的充分不必要条件，它将平稳分布与转移矩阵联系在一起

7.MCMC就是通过构建马尔可夫链概率序列，使其收敛到平稳分布p(z)

马尔科夫链蒙特卡洛方法，英文是Markov Chain Monte Carlo，简称MCMC。是一种随机性近似推断方法，它也是求解隐变量后验分布的一种推断方法，它核心思想是求得复杂概率分布下的期望值：

上一篇文章MCMC（蒙特卡洛采样）中，我们介绍了蒙特卡洛的拒绝采样和重要性采样，除了这两种，还有MCMC，它是基于马尔可夫链提出的，因此，先对马尔可夫链做一个深入介绍。

马尔可夫链

马尔可夫链，英文是Markov Chain，它由状态空间Val(X)和一个转移模型T定义，该模型对每个状态 x∈Val(X)，定义了下一状态在Val(X)上的分布。更准确地说，对于每对状态x，x'，转移模型T指定了从状态x到状态x'的概率P(x→x')。这个转移概率都适用于任何时候处于状态x 的链。

我们研究的是满足马尔可夫性质的马尔可夫链，也称为齐次(一阶)马尔可夫链。

所谓满足马尔可夫性质，是指：

当一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于现在状态；换句话说，在给定现在状态时，它与过去状态（即该过程的历史路径）是条件独立的，那么此随机过程即具有马尔可夫性质。

为了简便，我们把马尔可夫链简称为马氏链。它是一种时间和状态都是离散的随机变量序列。

马尔可夫链的状态关系可以用图形表示（示例）：

箭头表示状态间的转移概率(条件概率)，状态也可以转到自身，也就是某一状态在某一时刻以某种概率维持不变。每一个时刻都是所有状态的一个概率分布。加上时间属性后，马氏链的概率图模型可以表示如下：

这里需要说明一下的，假如马尔可夫链的状态是有限个，比如k个，不妨令它们分别为1,2,3,...k，那么，每个时刻的X都可以取k个状态的任意一个，也就是一种概率分布。比如在t=1时刻，X1状态是一个随机变量，它每种状态的取值对应一种概率：

X1	1	2	...	k
P1	a1	a2	....	ak

所有a之和就是概率为1，即a1+a2+..+ak=1.

同样，对于X2，也有一种概率分布：

 

X2	1	2	...	k
P2	b1	b2	...	bk

所有b之和就是概率为1，即b1+b2+..+bk=1.

也就是说，在每一刻时刻，序列变量X都是一个随机变量，它是所有状态的随机变量，但每个时刻对应的概率分布可能不一样。

转移矩阵

马氏链的转移矩阵是指，所有状态之间互相转换的概率构成的矩阵，设i和j是马氏链的两种状态，Tij表示从状态i转移到j的概率：Tij=P(X=j|X=i)。

我们把状态转移矩阵记为T=[Tij].

注：在一个马氏链中，转移矩阵是固定，每个时刻序列X的概率分布是变化的，这个要区分开

举个例子：

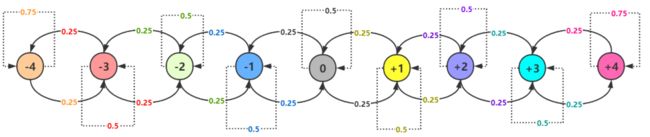
假设蚱蜢在一条直接的9个位置来回跳跃，我们把这9个位置记为蚱蜢所处的状态，用整数-4,-3,...,+4来表示，这些整数以点的形式排成一行。一个蚱蜢从这条线的位置0东摇西晃地出发。在每个时间点上，它以0.5的概率停留不动，或以相同的概率向左或向右跳。因此，P(i→i)=0.5，P(i→i+1)=0.25，以及P(i→i-1)=0.25。但是，因为处于两端的位置被墙所堵，所以P(+4→+4)=0.75,P(-4→-4)=0.75。我们可以把状态空间想象为一张图，具有对应于不同状态之间转移的概率加权有向边：

蚱蜢的马尔可夫链

蚱蜢每个时刻都会在处于某个状态，可以想象随机采样的一个过程，该过程定义了状态的一个随机序列：

因为转移模型是随机的，所以该过程在第t步的状态可以视为一个随机变量Xt.

假设初始状态X0是与某个初始状态分布一致的分布，那么上面的随机序列可以用链动态来定义：

蚱蜢例中，一共9个状态(-4,-3,...,+4)，其转移矩阵为：

平稳分布

我们继续蚱蜢的例子来引出平稳分布：

初始时，蚱蜢的位置是0，所以P(x0=0)=1;

在时刻t=1，X1以概率0.5为0，并且在位置+1或者-1的概率均为0.25;

在时刻t=2，X2以概率0.5²+2.0.25²=0.375为0，并且在位置+1或者-1的概率均0.25;

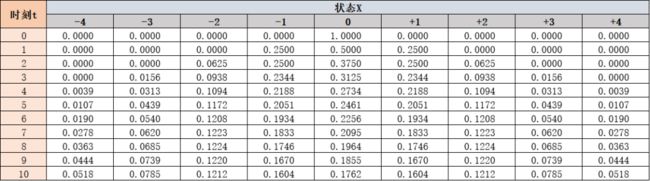
下表列出了t=0~10所处状态的概率大小.

随着过程继续，概率被分散到越来越多的状态上，它最终会达到一个平稳的状态，下表可以看到，在t=33时刻，每个状态的概率稳定在0.11.

随着时间的推移，如果马氏链的每个状态都会趋于一个稳定的数值，我们称过程收敛,也即：

在收敛处，我们希望产生的分布π(X)是相对于转移模型的平衡状态,也就是停留在某一状态的概率与从随机采样的前期状态转移到它的概率相同。

数学表示为：

记成积分形式为：

注：π的个数是指状态的个数，每一个π表示其概率；如果这里取有限个π，那么称为有限状态马尔科夫链。

就如上面蚱蜢的例子，每一个时刻的9个状态取值的概率不一致，但随着时间推移，在某个时刻t后，状态取值概率不变，即在t时刻未来的无穷个时刻里，每个状态的取值概率不变。我们要做的就是找到这个时刻及其对应的概率分布。

总结一句话：平稳分布就是表示在某一个时刻后，分布不再改变

而MCMC就是通过构建马尔可夫链概率序列，使其收敛到平稳分布p(z).

细致平衡

但并不是所有马氏链都是平稳分布，所以我们想找到一种构建有平稳分布的马氏链，在此前首先要证明马氏链有期望的平稳分布问题。

这个条件就是细致平衡（Detailed Balance）：

从细致平衡到平稳分布是一个充分不必要条件：

我们可以证明这一点：

这样，细致平衡条件将平稳分布的序列和⻢尔可夫链的转移矩阵联系在⼀起，把转移矩阵作为提议矩阵（提议函数），通过它可以不断⽣成样本点，就可以完成采样了。这个也就是MCMC的核心。至于如何生成，我们下一篇做详细介绍

参考资料：

《概率图模型原理与技术》