【图论】—— 有向图的强连通分量

---

给定有向图 ，若存在 ，满足从 出发能到达 中所有的点，则称 是一个“流图”（ Flow Graph ），记为  ，其中， 称为流图的源点。

在一个流图  上从  进行深度优先遍历，每个点只访问一次。所有发生递归的边  （换言之，从  到  是对  的第一次访问）构成一棵以  为根的树，我们把它称为流图  的搜索树。

同时，在深度优先遍历的过程中，按照每一个节点第一次被访问的时间顺序，依次给予流图中 N 个节点 1~N 的整数标记，称为时间戳，记为 。

流图中的每条有向边  必然是以下四种之一：

1. 树枝边，指搜索树中的边，即  是  的父节点
2. 前向边，指搜索树中  是  的祖宗节点
3. 后向边，指搜索树中  是  的祖宗节点
4. 横叉边，指除了以上三种情况之外的边，它一定满足  

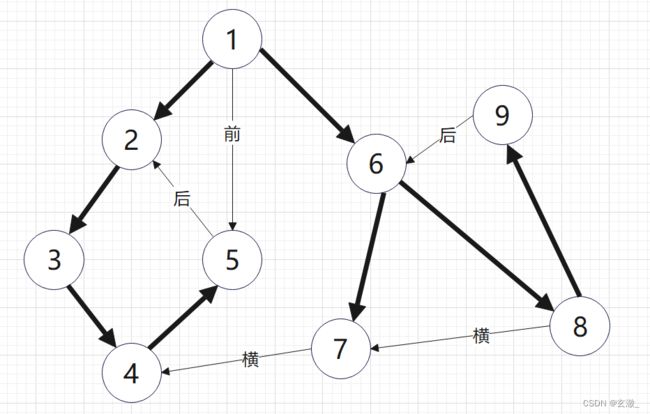
如下图“流图”以及其搜索树所示： 

加粗的表示的是树枝边，并构成一棵搜索树。 

---

有向图的强连通分量 

 给定一张有向图。若对于图中的任意两个结点 ，既存在从  到  的路径，也存在从  到  的路径，则称该有向图是“强连通图”。
 

有向图的极大连通子图称为“强连通分量”，简记为 SCC(Strongly Connected Component)。

此处的“极大”的含义和双连通分量的“极大”的含义类似。

Tarjan算法基于有向图的深度优先遍历，能够在线性的时间里求出一张有向图的强连通分量。

一个“环”一定是强连通图。如果既存在从  到 的路径， 也存在从  到  的路径，那么  显然在一个环中。因此，Tarjan算法的基本思路就是对每个点，尽量找到与它一起能够构成环的所有节点。

容易发现，“前向边”  没有什么用处，因为搜索树上本来就存在 从  到 的路径。

“后向边”  非常有用，因为它可以从搜索树上 从  到  的路径一起构成环。

“横向边”  视情况而定，如果从  出发能够找到一条回到  的祖宗节点，那么  就是有用的。

---

为了找到通过“后向边”和“横叉边”构成的换，Tarjan算法在深度优先遍历的同时维护一个栈。

当访问到结点 x 时，栈中需要保存以下两类节点：

1. 搜索树上 x 的祖宗节点，记为集合  
   
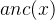
   设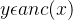  。若存在后向边  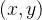，则 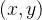 与 y 到 x 的路径一起形成环。
2. 已经访问过，并且存在一条路径到达 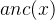 的节点
   
   设 z 是一个这样的点，从 z 出发存在一条路径到达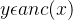  。若存在横叉边  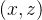，则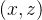 、z 到 y 的路径、y 到 x 的路径构成一个环。

综上所述，栈中的节点就是能与从 x 出发的“后向边”和“横叉边”形成环的节点。进而可以引入“追溯值”的概念。

---

追溯值

 设  表示流图的搜索树中以 x 为根的子树。x 的追溯值  定义为满足以下条件的节点的最小时间戳：

1. 该点在栈中
2. 存在一条从 出发的有向边，以该点为终点

根据定义，Tarjan算法按照以下步骤计算“追溯值”：

1. 当节点 x 第一次被访问时，把 x 入栈，初始化 
2. 扫描从 x 出发的每一条边 
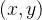
   1. 若 y 没有被访问过，则说明  是“树枝边”，递归访问 y ，从 y 回溯后，令
   2. 若 y 被访问过且 y 在栈中，则令 
3. 从 x 回溯之前，判断是否有  。若成立，则不断从栈中弹出节点，直至 x 出栈

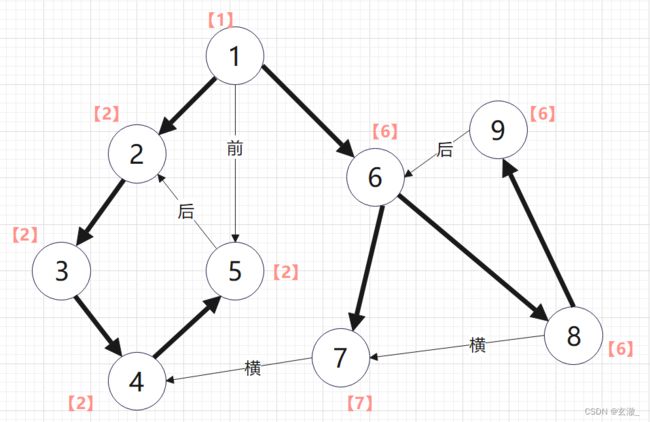
 下页图中的中括号【】里的数值标注了每个节点的的“追溯值”

---

强连通分量判定法则 

 在追溯值的计算过程中，若从 x 回溯前，有  成立，则栈中从 x 到 栈顶的所有节点构成一个强连通分量。

大致来说，在计算追溯值的第三步，如果  ，那么说明  中的节点不能与栈中其他结点一起构成环。另外，因为横叉边的终点时间必然小于起点时间戳，所以中的结点也不可能直接到达尚未访问的结点（时间戳更大）。综上所述，栈中从 x 到栈顶的所有节点不能与其他结点构成环。

由因为我们及时进行了判定和出栈操作，所以从 x 到栈顶的所有节点独立构成一个强连通分量。

 Tarjan算法模板

void tarjan(int u)
{
    dfn[u] = low[u] = timestamp;
    stk[++ top] = u, in_stk[u] = true;
    
    for(int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if(!dfn[j])
        {
            tarjan(j);
            low[u] = min(low[u], low[j]);
        }
        else if(in_stk[j])
            low[u] = min(low[u], dfn[j])
    }
    
    if(dfn[u] == low[u])
    {
        int y;
        ++ scc_cnt;
        do{
          y = stk[top ++ ];
          in_stk[y] = false;
          id[y] = scc_cnt;
        }while(y != u)
    }
}

---

缩点 

我们可以把每一个 SCC 缩成一个点。对于原图中的每条有向边  若  ，则在编号为  与编号为  的SCC之间连边。

最终，我们会得到一个有向无环图（DAG）

for(int x = 1; x <= n; i ++ )
    for(int j = h[i]; ~j; j = ne[j])
    {
        int y = e[j];
        if(id[i] == id[y]) continue;
        add(id[x], id[y]);
    }

---

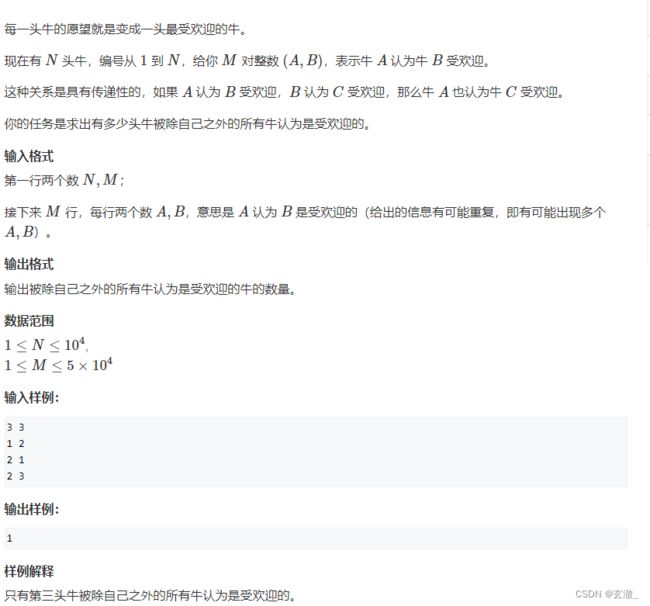
 例题：AcWing 1174. 受欢迎的牛

---

AC代码 

#include 
#include 
#include 
#include 

using namespace std;

const int N = 10010, M = 50010;

int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int stk[N], top;
bool in_stk[N];
int id[N], scc_cnt, Size[N];
int dout[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void tarjan(int u)
{
    dfn[u] = low[u] = ++ timestamp;
    stk[ ++ top] = u, in_stk[u] = true;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!dfn[j])
        {
            tarjan(j);
            low[u] = min(low[u], low[j]);
        }
        else if (in_stk[j]) low[u] = min(low[u], dfn[j]);
    }

    if (dfn[u] == low[u])
    {
        ++ scc_cnt;
        int y;
        do {
            y = stk[top -- ];
            in_stk[y] = false;
            id[y] = scc_cnt;
            Size[scc_cnt] ++ ;
        } while (y != u);
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    while (m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
    }

    for (int i = 1; i <= n; i ++ )
        if (!dfn[i])
            tarjan(i);

    for (int i = 1; i <= n; i ++ )
        for (int j = h[i]; ~j; j = ne[j])
        {
            int k = e[j];
            int a = id[i], b = id[k];
            if (a != b) dout[a] ++ ;
        }

    int zeros = 0, sum = 0;
    for (int i = 1; i <= scc_cnt; i ++ )
        if (!dout[i])
        {
            zeros ++ ;
            sum += Size[i];
            if (zeros > 1)
            {
                sum = 0;
                break;
            }
        }

    printf("%d\n", sum);

    return 0;
}