勘探开发人工智能技术:机器学习(2)
0 提纲
3.1 k k k 近邻算法
3.2 决策树
3.3 k k kMeans
3.4 如何定义机器学习问题
3.5 线性回归
1 k k k 近邻算法
开卷考试, 在桌上堆的资料越多, 越是 “见多识广”.
1.1 核心思想
具有讽刺意味的是: 机器学习最基本的算法居然是不学习, 也称为惰性学习 (lazy learning).
k k kNN ( k k k nearest neighbors) 通过计算样本间的距离 (相似度) 来确定待预测样本应与哪些训练样本的标签保持一致.
为了应对一场考试, 我们可以不学习, 而在考场上去翻书.
是的, 在解决实际问题时, 完全可以是开卷考试.
例子: 上午来了 60 个就诊者, 根据他们的各项检测指标 (即数据), 主治医生给出了诊断结论 (如是否患病, 以及患哪种病). 实习医生只是用小本本把带标签数据记录下来, 并没往心里去.
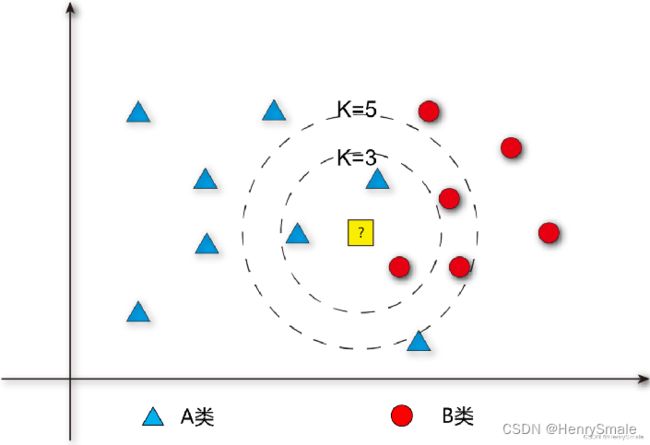
下午来了 1 个就诊者 A, 实习医生将他的检测指标与上午 60 个就诊者的数据逐一比对, 并找出 k k k = 3 个最相似的. 根据这 k k k 个就诊者的情况, 就可以对 A 的患病情况进行预测 (例如, 他们都没患病, 就预测 A 也没病).
这种方式极度简单, 但揭示了人类认识世界的一个本质而有效的思想: 根据相似性进行预测.
人们常说“见多识广”, 本质上就是大脑内存储的样本多, 就可以对新样本进行准确的判断.大医院的医生更靠谱, 一些小医院所说的疑难杂症, 对他们而言可能是天天见的病例. 因此, 在学习更多的算法之后, 仍然需要记住一句话: 永远不要小瞧 k k kNN. 你很难找到一种算法在随机选择的 100 个数据集上完美地打败它.
前段时间热炒的大数据概念, 其中一个思想就是: 如果训练数据的量足够大, 那么我们只需要用很简单方法 (如 k k kNN) 即可. 假设一个实习生见到的不是 60 个样本, 而是 1 亿个样本, 那么他的判断应该可以达到惊人的准确性.
西瓜书上也说了, 理论上可以证明, 当样本量足够大时, k k kNN 的误差不超过贝叶斯误差 (即理论最大误差) 的 2 倍.
1.2 参数选择
k k k 是一个需要调整的参数.
如果是二分类问题, 一般将其设置为奇数, 方便投票.
要知道 k k k 设置为多少合适, 可以使用验证集.
1.3 距离度量
距离公式的选择,比如欧几里得距离:
d ( x , y ) = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + ⋯ + ( x n − y n ) 2 = ∑ i − 1 n ( x i − y i ) 2 d(x, y)=\sqrt{\left(x_{1}-y_{1}\right)^{2}+\left(x_{2}-y_{2}\right)^{2}+\cdots+\left(x_{n}-y_{n}\right)^{2}}=\sqrt{\sum_{i-1}^{n}\left(x_{i}-y_{i}\right)^{2}} d(x,y)=(x1−y1)2+(x2−y2)2+⋯+(xn−yn)2=i−1∑n(xi−yi)2
假设就诊者 x 1 x_1 x1和 x 2 x_2 x2的 3 项检测指标值分别为 [ 0.3 , 1.7 , 380 ] 和 [ 0.25 , 1.9 , 400 ], 则它们的欧氏距离为:
d ( x 1 , x 2 ) = ( 0.3 − 0.25 ) 2 + ( 1.7 − 1.9 ) 2 + ( 380 − 400 ) 2 d(x_1, x_2)=\sqrt{\left(0.3-0.25\right)^{2}+\left(1.7-1.9\right)^{2} +\left(380-400\right)^{2}} d(x1,x2)=(0.3−0.25)2+(1.7−1.9)2+(380−400)2
曼哈顿距离为:
d ( x 1 , x 2 ) = ∣ 0.3 − 0.25 ∣ + ∣ 1.7 − 1.9 ∣ + ∣ 380 − 400 ∣ d(x_1, x_2)=\left|0.3-0.25\right|+\left|1.7-1.9\right| +\left|380-400\right| d(x1,x2)=∣0.3−0.25∣+∣1.7−1.9∣+∣380−400∣
1.4 主要缺点
慢
试想别人学习到知识, 考试的时候刷刷地做题, 而你要一页页地翻书, 速度就不是一个量级的了.
为了缓解这个问题, 可以先把 10,000 条训练数据聚为 50 个簇, 每簇约 200 个样本 (聚类问题), 并获得这些簇中心点. 进行比对的时候, 先确定与哪个簇中心最近, 然后再在这个簇中心找邻居. 这样就可以把 10,000 次对比降为约 50 + 200 次.
1.5 归一化
从 上面的距离公式可以看出, 由于最后一个指标的值比较大, 前面两个指标对距离的贡献几乎可以忽略不计. 甚至这种指标值大小是由单位所导致的 (如毫升与升).
为消除不同指标取值范围的影响, 可使用归一化, 即所有指标均取 [ 0 , 1 ] [0, 1][0,1] 区间的值. 例如, 第 3 项指标的最大值是 500, 最小值是 100, 则数据 380 归一化变为:
380 − 100 500 − 100 = 280 400 = 0.7 \frac{380-100}{500-100} = \frac{280}{400} = 0.7 500−100380−100=400280=0.7
1.6 度量学习
归一化还是会引入新的问题: 认为所有的指标同等重要. 在现实应该中, 应该为每个指标赋予一定的权值 w w w, 并使得该指标的取值范围成为 [ 0 , w ] [0, w] [0,w].
相应的权值可以从数据中学习到. 这就是度量学习的初衷.
1.7 常见误区
- 小瞧 k k kNN, 觉得它过于简单.
- 没有认识到 k k kNN 正是人类认识物体的基本方式.
- 不知道 k k kNN 可以做回归 (把邻居的实数型标签值取平均即可).
1.8 例子
2 决策树
将 “如果-那么” 组织成决策树, 它是人类最容易理解与传授的知识.
2.1 结构
决策树是一种与人类思维一致, 可解释的模型.
人类的很多知识以决策规则的形式存储:
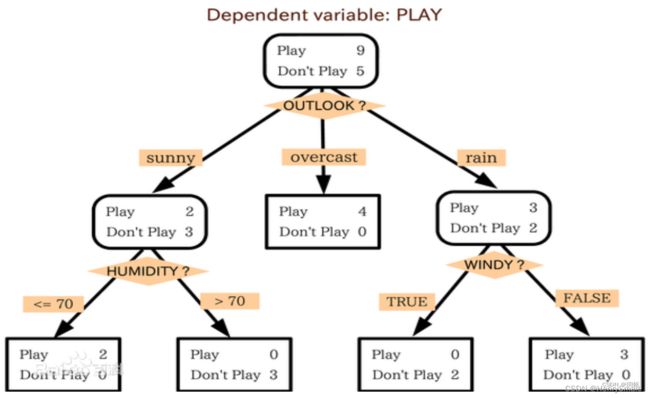
- 如果今天是阴天 (outlook = overcast), 就去打球.
- 如果今天出太阳 (outlook = sunny) 而且湿度不高于 70% (humidity ≤ 70), 就去打球.
- 如果今天出太阳 (outlook = sunny) 而且湿度高于 70% (humidity > 70), 就不去打球.
2.2 优势
直观, 易于理解, 易于传授: 学生会迅速掌握这棵树.
相比于决策规则集合, 决策树的优点是没有死角: 任何一种情况都被覆盖.
与前面的 k k kNN 相比, 它是一个真正的模型 (model), 预测阶段脱离了训练数据.
对于机器而言, 使用决策树进行预测非常迅速, 任何新的实例, 都对应于从树根走到某个叶节点的一条路径. 这种路径的长度通常不超过 10.
2.3 原理
人为可以构建决策树, 这就是专家知识, 但它不属于我们重点讨论的内容.
从数据中构建出决策树, 才是机器学习的内容.
决策树的构建过程, 实际上是一个不完全归纳 (特殊到一般) 的过程. 为学习到图 1 所示的决策树, 只用了 14 个样本. 但这棵决策树所覆盖的可能情况, 远远超过了 14. outlook 有 3种情况, humidity 有 100 种情况, rain 有 2种情况, windy 有 2 种情况, 所以总共是 3 × 100 × 2 × 2 = 1200 3 × 100 × 2 × 2 = 1200 3×100×2×2=1200 种情况.
决策树构建的原则是: 越小越好, 即节点树越少越好. 这是基于奥克姆剃刀 (Occam’s razor) 原理.
2.4 构建方法
穷举法. 由于数据量比较大, 一般不使用这种方法.
启发式方法. 如基于信息熵、基于基尼指数.
- ID3 适用于枚举型数据, 使用了信息熵 (条件信息熵之差称为信息增益).
- 对于实数型数据, 则使用 C4.5.
- 在绝大多数情况下, ID3 可以获得最小的决策树.
- 在 2000 年前, 决策树火得一蹋糊涂.
剪枝. 如果一棵决策树使用一张 A4 纸都画不下, 就失去了泛化能力. 这时候需要剪枝. 例如, 在一个节点处, 有 100 个正样本和 1 个负样本, 虽然可以增加一个属性将它们分开, 但最好不要增加这个属性, 这样节点至少节约了一个.
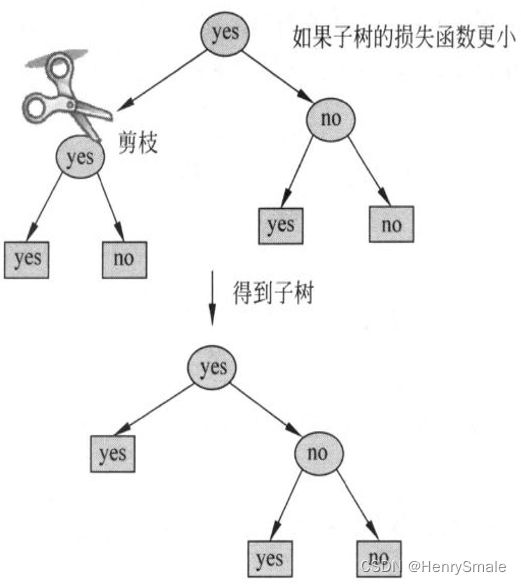
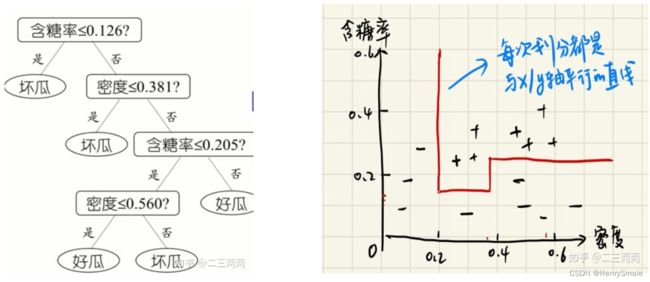
常规的决策树, 其分割面都垂直于相应特征的坐标轴.
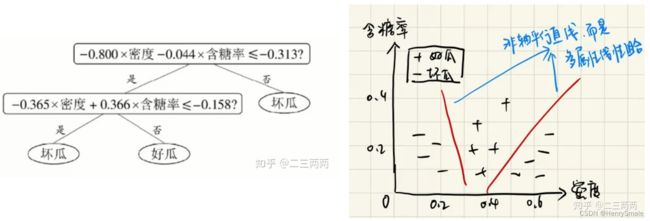
有时候想同时考虑多个属性组合而成 (温度 + 湿度) 的新属性, 可以使用 Oblique decision tree (斜决策树),也称为多变量决策树.
3 k k kMeans
适用于球形数据, 即每个数据点到其所在簇的中心都不远.
3.1 基本思想
k k kMeans 是数据分布未知时最合适的聚类算法.
- 最大化簇的内聚性 (即同一簇的点距离较近), 最小化簇间的耦合性 (即不同簇的点距离较远).
- 其优化目标可以写为:
min ∑ i d ( x i , c ( x i ) ) (1) \min \sum_i d(x_i, c(x_i)) \tag1 mini∑d(xi,c(xi))(1) - 其中 c ( x i ) c(x_i) c(xi) 是第 i i i 个对象 x i x_i xi所处的簇的中心 (即将该簇所有点的特征值取平均获得的虚拟中心).
3.2 算法
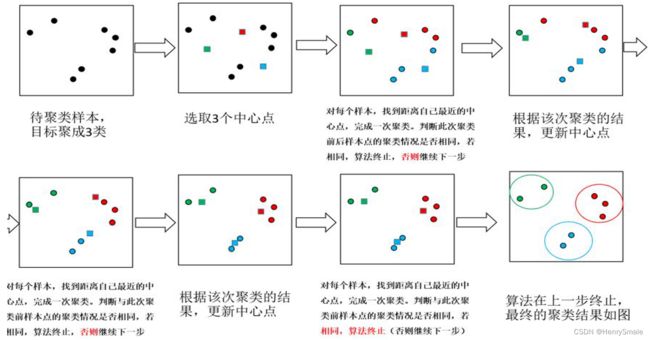
Step 1. (确定老大) 随机选择 k k k个点作为中心点.
Step 2. (分派别) 对于任意对象, 计算它到这 k k k个点的距离, 离谁最近, 就与它属于同一簇.
Step 3. (重新选择老大) 每个簇求虚拟中心, 将其作为老大.
Step 4. (判断是否收敛) 如果本轮的中心点与上一轮的中心点相同, 则结束; 否则转 Step 2.
3.3 算法特点
与 k k kNN 的共同点在于, 都使用某个距离度量.
涉及迭代, 因此比 k k kNN 复杂.
初始点的选择会影响最终的结果. 很可能只收敛到局部最优解.
适合"球型"数据. 即每一簇从三维的角度来看都像一个球. 而并不适合于有较多离群点的数据. 所谓离群点, 可以认为是指离所有聚类中心的都挺远的数据点. 它会对 k k kMeans 的重心计算产生较大影响.
并不是在所有的数据集上, 都能很快收敛. 我试过的数据中, 有 50 轮都未收敛的, 干脆就凑合了.
3.4 参数设置与距离度量
只有一个 k k k.
显然, k k k 越大, (1) 式的值就越小. 确定 k k k 值多大合适, 有可能比确定如何聚类更困难.
距离度量参见 k k kNN. 这方面两个算法确实相同.
3.5 简单改进
删除离群点.
多次初始化聚类中心点, 选择 (1) 式最小化那个. 当数据集不大的时候, 局部最优解的个数并不多.
3.6 常见误区
不知道 k k kMeans 是有优化目标的 (反正我初学的时候就不知道).
不知道 k k kMeans 仅保证局部最优.
小瞧了 k k kMeans 的适应性 (与小瞧 k k kNN 同理).
3.7 例子
4 如何定义机器学习问题
输入、输出、优化目标、约束条件, 不能用这个范式抽象的实际问题, 几乎无法使用机器学习解决.
4.1 机器学习问题定义的模式
做研究应该以问题为导向. 机器学习问题定义清楚了, 才能保证在解决它的过程中不出大的偏差.
多数机器学习问题可以按照如下约束满足问题 (Constraint Satisfaction Problem) 进行定义:
- 输入.
- 输出.
- 优化目标.
- 约束条件.
看上去平平无奇. 只有你自己去面对具体的问题, 才会知道是否思路清晰, 心如磐石.
4.2 例子1:最优决策树构建
- 输入: 结构化数据, 其中特征均为枚举型.
- 输出: 决策树.
- 优化目标: 最小化叶节点数量.
- 约束条件: 与训练集的所有数据相容, 即在训练数据上的分类准确率为 100%.
有些训练数据本身有冲突对象, 即特征相同 (检测指标相同), 但标签值不同 (有的患病, 有的不患病), 这涉及数据的不确定性. 这时可以把约束条件改为优化目标, 即最大化在训练数据上的分类准确率.
4.3 例子2:最优聚类
- 输入: 结构化数据, 其中特征均为实型;簇数 k k k.
- 输出: 每个实例的簇编号 (1 到 k k k).
- 优化目标: 每个实例到簇中心的距离和
说明: 优化目标也可以写成簇内每对实例的距离之和. 但这样计算量要大得多. 例如, 1,000 个实例分成 10 个簇, 每个簇刚好有 100 个实例. 则计算实例到中心的距离只需要进行 1,000 次距离计算, 而计算实例对的距离, 需要 10 * C(100, 2) = 500*99 次.
4.4 问题定义并不决定解决方案
在解决机器问题的时候, 我们很可能不按严格按照定义来设计算法, 因为这涉及模型的泛化性.
5 线性回归
将数据点串成一根糖葫芦.
5.1 一元线性回归
线性回归是直接从问题到解决方案, 而岭回归之类则让我们理解正则项.
在二维平面有一系列数据点, x x x坐标表示其数据, y y y 坐标表示其标签. 对于新的数据, 如何预测其标签? 为此, 我们可以建立一个线性函数 y = a x + b y=ax+b y=ax+b.
- 输入:数据点集合 { ( x i , y i ) } i = 1 n \{(x_i, y_i)\}_{i = 1}^n {(xi,yi)}i=1n.
- 输出: 线性函数的 a , b a, b a,b.
- 优化目标: min ∑ i = 1 n ( y i − y i ′ ) 2 \min \sum_{i = 1}^{n} (y_i - y_i')^2 min∑i=1n(yi−yi′)2, 其中 y i ′ = a x i + b y_i' = a x_i + b yi′=axi+b.
这个问题在高中学过, 称为最小二乘法. 从优化目标可以看出, 优化的是 l 2 l_2 l2模.
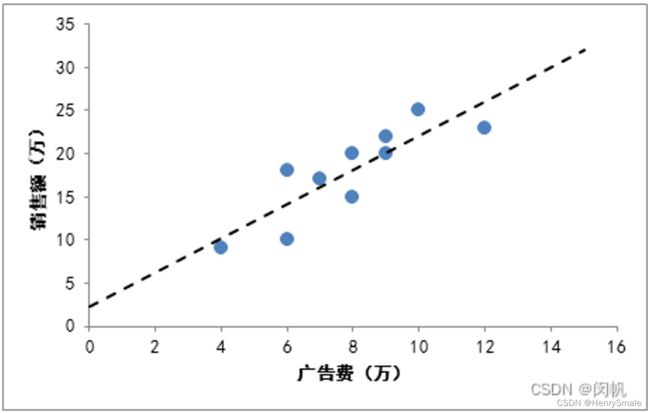
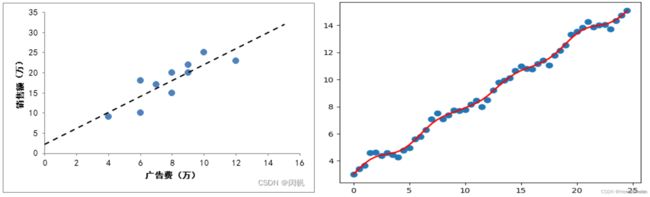
下图给出了广告费与销售额之间的关系. 虚线所示的 f ( x ) f(x) f(x) 试图对所给的数据点进行拟合. 由此可以预测广告费为 2 万元、14万元等所对应的销售额. 直观地看, a a a 是斜率, b b b 是偏移量.
5.2 多元线性回归
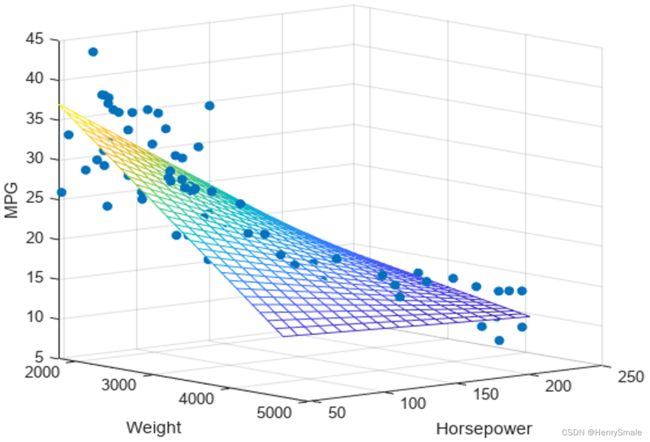
多元的情况, 只需要将 x x x 和 a a a 从标量改为向量即可. y y y 与 b b b仍然为标量. 这时, 拟合直线换成了超平面.
- 输入:数据点集合 { ( x i , y i ) } i = 1 n \{(x_i, y_i)\}_{i = 1}^n {(xi,yi)}i=1n, 其中 x i ∈ R m x_i \in \mathbb{R}^m xi∈Rm.
- 输出: 线性函数的 a , b \mathbf{a}, b a,b.
- 优化目标: min ∑ i = 1 n ( y i − f ( x i ) ) 2 \min \sum_{i = 1}^{n} (y_i - f(x_i))^2 min∑i=1n(yi−f(xi))2, 其中 f ( x i ) = a x i + b f(x_i) = \mathbf{a} \mathbf{x}_i + b f(xi)=axi+b.
为了解该问题, 可以将数据集合用矩阵表示, 标签集合则用向量表示, 即
Y = X θ + b . \mathbf{Y} = \mathbf{X} \theta + b. Y=Xθ+b.
在 $ \mathbf{X}$ 最左边加上一列全 1, 可以把 b b b 吸收进 θ \theta θ 里面去, 获得:
Y = X θ . \mathbf{Y} = \mathbf{X} \theta. Y=Xθ.
例如:
X = [ 1 0.2 0.4 0.3 1 0.3 0.5 0.4 1 0.3 0.7 0.5 1 0.4 0.6 0.6 1 0.2 0.8 0.6 ] , Y = [ 0.2 0.3 0.7 0.4 0.5 ] (2) \mathbf{X}=\left[\begin{array}{llll} 1 & 0.2 & 0.4 & 0.3 \\ 1 & 0.3 & 0.5 & 0.4 \\ 1 & 0.3 & 0.7 & 0.5 \\ 1 & 0.4 & 0.6 & 0.6 \\ 1 & 0.2 & 0.8 & 0.6 \end{array}\right], \mathbf{Y}=\left[\begin{array}{l} 0.2 \\ 0.3 \\ 0.7 \\ 0.4 \\ 0.5 \end{array}\right] \tag2 X= 111110.20.30.30.40.20.40.50.70.60.80.30.40.50.60.6 ,Y= 0.20.30.70.40.5 (2)
由于实例个数 (这里 n = 5 n = 5 n=5) 多于特征个数 (这里 m = 3 m = 3 m=3), (2) 式是一个超定方程组, 即一般情况下不存在这样的 θ \theta θ 使得 (2) 式成立.
为了理解这个事情, 可以回到一元线性回归, 当数据点 3 个或以上, 就不存在一条直线刚好穿过所有的点.
根据优化目标, 可以解得:
θ = ( X T X ) − 1 X T Y . \theta = (\mathbf{X}^\mathbf{T}\mathbf{X})^{-1}\mathbf{X}^\mathbf{T}\mathbf{Y}. θ=(XTX)−1XTY.
如果这里求矩阵的逆出了问题 (有些矩阵没有逆), 就可以用梯度下降法来求解.
5.3 岭回归
θ = ( X T X ) − 1 X T Y . \theta = (\mathbf{X}^\mathbf{T}\mathbf{X})^{-1}\mathbf{X}^\mathbf{T}\mathbf{Y}. θ=(XTX)−1XTY.
上面公式求逆矩阵的时候可能出问题, 为了解决它, 引入新的优化目标:
min ∑ i = 1 n ( y i − f ( x i ) ) 2 + λ ∑ j = 1 m θ j 2 . \min \sum_{i = 1}^{n} (y_i - f(x_i))^2 + \lambda \sum_{j = 1}^{m} \theta_j^2. mini=1∑n(yi−f(xi))2+λj=1∑mθj2.
由此推导出:
θ = ( X T X + λ I ) − 1 X T Y . \theta = (\mathbf{X}^\mathbf{T}\mathbf{X} + \lambda \mathbf{I})^{-1}\mathbf{X}^\mathbf{T}\mathbf{Y}. θ=(XTX+λI)−1XTY.
- λ I \lambda \mathbf{I} λI 的加入使得矩阵一定可逆.
- 除了解决矩阵求逆的问题, 新的优化目标还有个非常重要的作用: 对 θ j \theta_j θj的值进行惩罚. 也就是说, θ j \theta_j θj的绝对值越大, 这个方案越不好.
- λ ∑ j = 1 m θ j 2 \lambda \sum_{j = 1}^{m} \theta_j^2 λ∑j=1mθj2就是传说中的正则项, 它牺牲了模型在训练集中的拟合能力, 但提升了在新数据上的预测能力 (即泛化能力). 而模型的泛化能力是机器学习的核心.
- 这里的系数 λ \lambda λ 设置得越大, 对训练数据的拟合就越差. 但设置得太小, 就不能达到控制过拟合的目的.
- 很多机器学习的论文, 都致力于提升模型的泛化能力. 俗气一点, 就是使用不同的正则项, 然后再给出合理的解释, 并用良好的实验结果来证实. 系数 λ \lambda λ 的设置, 也通常是人为的.
5.4 欠拟合
左图所示的糖葫芦串得不错, 但在现实世界中, 用一根直接把数据串起来很困难. 这很容易导致欠拟合, 也就是说, 很多点都拟合得不好.
局部线性回归:数据往往体现一定的局部性, 即与自己相邻的数据, 影响更大 (回头想想 k k kNN). 所以我们可以更重视局部点的影响, 由此引入局部线性回归, 如右图所示.
5.5 离群点
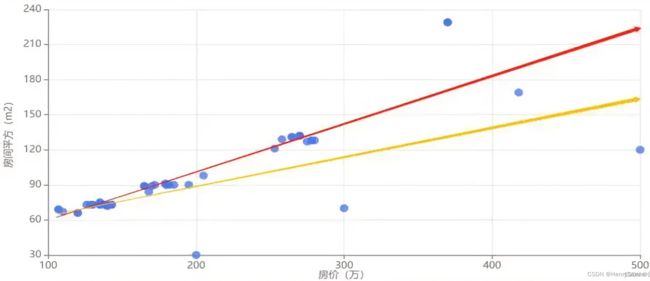
如图所示, 少量离群点导致拟合函数产生了较大的偏移 (下面这根线). 这些离群点可能是数据采集过程中错误导致.
一种解决方式如下: 生成拟合函数后, 可以把偏差最大的一部分 (如 1%) 训练数据去掉, 再进行拟合 (上面这根线). 这种简单的方式可以削弱离群点的影响.
5.6 线性回归在机器学习常识中的意义
是机器学习问题定义的一个典型案例.
线性模型及其变种在很多地方被采用. 也不是因为线性模型的拟合能力强 (其实它是最弱的), 而是因为它简单, 易于计算.
给出了一个典型的优化目标.
能从优化目标直接获得最优解, 如下式所示.
θ = ( X T X ) − 1 X T Y . \theta = (\mathbf{X}^\mathbf{T}\mathbf{X})^{-1}\mathbf{X}^\mathbf{T}\mathbf{Y}. θ=(XTX)−1XTY.
对于绝大多数机器学习问题, 这点无法做到.
给出了一个典型的正则项.
5.7 常见误区
- 可视化的时候, 标签本身需要占一个维度. 仅 1 个特征的时候,就需要在二维平面上表示. 例中有 3 个特征, 应该使用 4 维空间中的超平面表示. 这与后面的分类问题很容易弄混.
- X \mathbf{X} X 最左边一列为 1, 实际是为了把偏移量放入 θ \theta θ , 方便表达. 并不是数据多了一个特征.
- 超定方程组不存在解. 误差是难免的. 下面的公式理论上使得误差最小.
θ = ( X T X ) − 1 X T Y . \theta = (\mathbf{X}^\mathbf{T}\mathbf{X})^{-1}\mathbf{X}^\mathbf{T}\mathbf{Y}. θ=(XTX)−1XTY. - 系数 λ \lambda λ 的大小表示对过拟合的控制强度.
- 从一元线性回归来看, 误差不是点到拟合直线的距离, 而是 y i y_i yi与 f ( x i ) f(x_i) f(xi) 的差值.