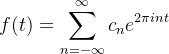Fourier变换极其应用(Brad G. Osgood)——第1章——Fourier级数(附录)
目录
1.8 附录：关于傅里叶级数收敛性的注解(Notes on the Convergence of Fourier Series)
1.8.1 借助Dirichlet核研究部分和:回到蜂鸣声问题(Sdudying partial sum via Dirichlet kernel:The buzz is back)
1.8.2 收敛速度和平滑度:Fourier系数有多大？(Rates of convergence and smoothness: How big are the Fourier coefficients?)
1.8.3 复指数真的是L2编辑 ([0,1])的一个正交基吗？(The complex exponentials really are an orthonormal basis for L2编辑 ([0,1] ?)
1.8.4 附录：逐点收敛对比一致收敛(Appendix: Pointwise convergence vs. uniform convergence)
1.9 附录：Cauchy-Schwarz 不等式(Appendix: The Cauchy-Schwarz Inequality)
1.9.1 L2编辑 ([0,1] 的Cauchy-Schwarz 不等式(Cauchy-Schwarz for L2编辑 ([0,1])
1.9.2 Fourier系数适用Cauchy-Schwarz不等式很好(The Fourier coefficients are fine)
1.9.3 卷积也适用Cauchy-Schwarz不等式(And convolution is also OK)
1.9.4 平方可积意味着可积(Square integrable implies integrable)
1.8 附录：关于傅里叶级数收敛性的注解(Notes on the Convergence of Fourier Series)
我的第一条评论是：“不要去那里。” 或者至少谨慎行事。自从Fourier因其发现的方法的普遍性而震惊了法国社会以来，关于Fourier级数收敛性的问题一直是数学分析中最棘手的问题之一(注：戏剧化的叙述会让你相信这种方式会导致疯狂。可怜的格Georg Cantor遭受了惨重的痛苦，但这并不是因为Fourier级数的收敛。真的，不是因为Fourier级数)。在这里我们将非常谨慎，而稍微谷歌一下就会很快找到你想知道的，或者找到比你相知道的还更丰富的资料。我们将给出一些解释，一些参考资料，但不会提供完整的证明，甚至不会提供完整的证明介绍。将本节视为您在其他地方可能会遇到的术语的介绍，并展示一些结论，如果有数学家偷偷接近(sneaks up)您，您可以使用这些结果进行自卫(译注：表示知道这些数学知识)。
无穷级数的收敛总是关于部分和的收敛。在 Fourier级数的背景下，就意味着对于函数 f ( t ),讨论其部分和
的收敛性,这个动作发生在 0 ≤ t ≤ 1 上。问题是，当 N ⟶ ∞ 时，在部分和上会发生什么。大致说来，有三种好事：
(1) 逐点收敛(Pointwise convergence) 。
插入一点 t , 我们有 
, 但是我们不会说太多，例如，关于从一点到下一点的收敛速度。
(2) 一致收敛(Uniform convergence) 。
这点比逐点收敛强烈。除了表述对于某个 t ∈[0,1] 有 ，还表述了当N ⟶ ∞ 时，有 
。换句话说，当 N 变大的时候，这个部分和 
在整个 0 ≤ t ≤ 1 上都保持贴近 f ( t )，从中，产生了这个描述子(descriptor)“一致(uniform)”,例如，“一致接近(uniform close)”，更多细节参见1.8.4节(译注：“一致”的直观体现是，在整个区间上，级数和函数都是贴近状态，不存在个别地方距离很大的情况)。
(3) 在 ![L^{2}[0,1]](http://img.e-com-net.com/image/info8/ffec041e2b454c5ab6e8677b0e55e03a.png){kind=small}
上收敛。
这就是我们上一节刚刚讲完的内容。条件是
。
更多完整的定义需要熟练地应用 ε和δ描述法，如果你选修数学分析课程，你就会受到这些方法和术语的打击。(注：但这可能是一次值得的打击。 我的同事Stephen Boyd曾是一名数学专业的学生，他希望他所有的博士生都进行分析，不是因为他们会使用具体的结果，而是因为这门课程所带来的清晰的思想。我对这个课程也抱有一些希望。)
在这三种模式中，一致收敛是最强的，因为它隐含了其他两种模式。逐点收敛是从 1.5.1 节中的定理获得的收敛类型，并且在跳跃不连续处，部分和实际上收敛到跳跃的平均值。 一致收敛需要比分段连续性更高的平滑性(该定理中的假设)。第 1.8.2 节中将有一个与此相关的定理。
看起来， 
收敛作为均值收敛的一种，与插入特定 t 值时部分和发生的情况无关。 然而，有一些定理确实解决了这种联系，而且它们是商业中最困难和最微妙的定理之一。
1.8.1 借助Dirichlet核研究部分和:回到蜂鸣声问题(Sdudying partial sum via Dirichlet kernel:The buzz is back)
回顾 1.6 节，分别讨论蜂鸣声信号和卷积。他们将以一种最有趣的方式出现在一起，尤其是对于电气工程师来说。
如果您有一些信号处理背景，您可能会认识到部分和
就是应用低通滤波器到完整Fourier级数
产生的结果。从–N到N的低频率部分保形“通过”，而低于–N 或高于 N 频率的部分被清零了。
这是怎么实现的？是通过与Dirichlet核
的卷积运算来实现的。
回顾一下，当两个周期信号进行卷积运算时，是它们的Fourier系数相乘。在这种情况下，对
于 
和 f ( t ),
。
但是，
。
因此，
的Fourier级数是
。
这便是低通滤波器。
我在数学专业的时候从未见过这样的描述。我们将再次看到低通滤波器，涉及Fourier变换。
作为一个积分(注：如果你已经在怀疑为什么 称为“核(kernel)”，其原因在于这个方程。就在此时此刻，
出现在积分中，对 f (τ)积分产生一个 t 的函数。在某些数学领域，t 的函数按积分表达式 
定义(卷积便是一个例子)，函数 k(t ,τ)称为一个核。我们将在第7章看到这一点。现在你知道了。在另一方面，我不知道这个专用词“kernel”出自何处。
。
针对 还有另一种写法，事实证明它对于分析 的收敛性更有帮助(注：我并不是说这些都是显而易见的事情，只是说“事实证明它会更有帮助”，正如我们将看到的。一起去兜风； 很快就会结束。)。因为 是偶数， 
，使用变量替换 u = τ – t 给到
---------------------------------
---------------------------------
。
最后这个等式成立，因为， 
是周期为1的周期函数，所以在任意长度为1的区间上积分都能得出同样的答案。
现在，请记住，我们不仅想知道当 N ⟶ ∞ 时 收敛，我们还想知道它收敛于 f (t)(或者在有跳跃点的不连续情况下，收敛于平均值)。为了帮助理解这一点，还有一个技巧。我们想到，
我们有
。
因此，
---------------------![=\int_{0}^{1}D_N(u)[f(t+u)-f(t)]du](http://img.e-com-net.com/image/info8/651a2a461c5f4345857597a456974a88.png){kind=small}
。
最后，回到 
作为一个正弦比的封闭形式的表达式，将变量 u换回τ ，因为它看起来更好，将积分限改为从-1/2到1/2(根据周期性是可行的),因为这样将使得后续的分析更容易：
![S_{N}(t)-f(t)=\int_{-1/2}^{1/2}\frac{sin[2\pi \tau(N+1/2)]}{sin(\pi \tau)}[f(t+\tau)-f(t)]d\tau](http://img.e-com-net.com/image/info8/10b17f1ee80f45b383e8bcc2e4a19027.png){kind=small}
。
正是这个表达式用于证明关于 
的结论。
非常简单，这就是原因。 收敛定理中的假设、1.5.1 节中的定理以及下一节中的定理都涉及 f ( t )的局部属性(local property)，例如一点的连续性、跳跃不连续性和一点的可微性。对于固定点 t，这意味着当 τ 很小时，查看 f ( t + τ ) - f ( t )。这种思想是取一个足够小的δ > 0 , 并将积分分段：
基于 f ( t ) 的合理假设，就像我们在逐段连续性和可微性上看到的那样，加上Dirichlet核的显式形式，使得当 N ⟶ ∞ 时估算积分并证明收敛成为可能。您对不同的积分使用不同的估算。根据假设，我们可以推导出逐点收敛或更强的一致收敛。
如果这是一门常规数学课程，我会给出完整的论据并做出估算，这是我一直喜欢的。但这不是一门常规数学课程，因此如果您想了解更多信息，我现在将让您查阅文献。除了许多专门讨论Fourier级数的书籍之外，许多介绍性数学分析的书籍都包含有关Fourier级数的一章，并将从我们上次停下的地方继续(注：如果您确实进行了查找，请注意不同的归一化(即不同的周期选择)将影响Dirichlet核。例如，如果作者使用周期为 2π 的周期函数，则相应的Dirichlet核为 
。Peter Duren 的 <
1.8.2 收敛速度和平滑度:Fourier系数有多大？(Rates of convergence and smoothness: How big are the Fourier coefficients?)
假如我们有一个平方可积的函数 f ( t )的Fourier级数
。
如前所述，根据 Bessel 不等式，当 n ⟶±∞ 时，
。
知道Fourier级数趋近于 0 ,我们能说出趋近速度有多快吗？
这是一种简单的方法，它给出了答案的一些意义，并展示了答案如何取决于函数或其导数的不连续性。所有这些讨论仅基于具有定积分的分部积分。
与往常一样，假设 f ( t ) 是周期 1 的周期性。在本次讨论中，我们假设函数不会在端点 0 和 1 处跳转，并且任何问题点都在区间内(注：这确实不是一个限制。 我只想处理一个不连续性，以便后面的论证)。也就是说，我们“ 重新想象一下，在 
在 
处可能会出现问题，因为也许 f ( t ) 会跳到那里，或者 f ( t ) 在 处是连续的，但有一个拐角，所以 f ( t )会跳 在 处是连续的，但有一个拐角，所以 f ( t )会跳在
。
为了分析 附近的状况，将其写成两个积分和的形式：
。
对以上每一个积分应用分部积分法。这样做时，我们假设函数至少在远离 的地方具有我们想要的任意数量的导数。然后，在第一次通过时，
![\int_{0}^{t_0}f(t)e^{-2\pi int}dt=[\frac{e^{-2\pi int}f(t)}{-2\pi in}]_{0}^{t_0}-\int_{0}^{t_0}\frac{e^{-2\pi int}f'(t)}{-2\pi in}dt](http://img.e-com-net.com/image/info8/cf0572be481c49a7b89cad1c8b5b3fee.png){kind=small}
![\int_{t_0}^{1}f(t)e^{-2\pi int}dt=[\frac{e^{-2\pi int}f(t)}{-2\pi in}]_{t_0}^{1}-\int_{t_0}^{1}\frac{e^{-2\pi int}f'(t)}{-2\pi in}dt](http://img.e-com-net.com/image/info8/e9e31cfcd2c84c878a6cac9fa474f6e5.png){kind=small}
，
将这些等式加起来。使用 f ( 0 ) = f (1 ) ，结果是
![\widehat{f}(n)=[\frac{e^{-2\pi int}f(t)}{-2\pi in}]_{t_{0}^{+}}^{t_{0}^{-}}-\int_{0}^{1}\frac{e^{-2\pi int}f'(t)}{-2\pi in}dt](http://img.e-com-net.com/image/info8/2ccdd5c30e544b7b844d4c698c76dada.png){kind=small}
，
其中，符号 
和 
表示，当我们在 点取左右极限的时候，我们正在考察 f ( t )的值。如果 f ( t ) 在 是连续的，则括号中的项消没，对于 
就仅剩下积分表达式。但如果 f ( t ) 在
点是不连续的(例如，存在跳跃点)，则这一项不会消没，则我们预计Fourier系数的大小为 1/ n 阶(注：如果我们有更多的跳跃不连续点，我们会将积分分解为几个子区间，并且我们会有多个 1/n 阶项。组合结果仍为 1/n 阶。如果函数在端点 0 和 1 处跳转，情况也是如此。)。
现在，假设 f ( t ) 在 点是连续的,并进行第二次分部积分。以和上面同样的方式，给出
![\widehat{f}(n)=[\frac{e^{-2\pi int}f'(t)}{(-2\pi in)^{2}}]_{t_{0}^{+}}^{t_{0}^{-}}-\int_{0}^{1}\frac{e^{-2\pi int}f''(t)}{(-2\pi in)^{2}}dt](http://img.e-com-net.com/image/info8/0bdec3bb997f4a3cb95c4660b6ba8e6d.png)
。
若 
(一阶导数)在 点是连续的,则括号中的部分消没。若 在 点是不连续的，例如，若在 点处存在拐角，则这一项不会消没，则我们预计 Fourier系数的大小为 
阶。
我们可以继续按这样的方式进行下去。大致的经验法则可以表述如下：
如果 f ( t ) 不连续，则Fourier系数应该具有一些类似 1/n 的项。
如果 f ( t ) 在除了拐角( f ( t )连续但其导数不存在)之外处处可微，则Fourier系数应该具有一些类似 的项。
如果 
存在但不连续，则Fourier系数应该具有一些类似 
的项。
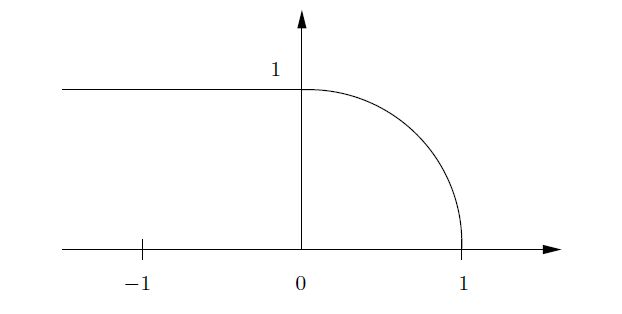
中的不连续性更难以可视化； 就图表而言，它通常是曲率的不连续性。 例如，想象一条曲线，由一段圆弧和一条在其端点与圆弧相切的线段组成。类似下面的图。
-------------------------图11. 不连续性示意图---------------------
曲线及其一阶导数在切点处连续，但二阶导数有跳跃。如果您以恒定速度沿着这条路径骑行，当您经过切点时，您会感到猛拉的感觉——加速度的不连续性。
显然，这种模式扩展到高阶导数的连续性/不连续性。它也与我们之前的一些例子相吻合。方波
具有跳跃不连续点，其Fourier 级数是
![\displaystyle \sum_{n=odd}^{}\frac{2}{\pi in} e^{2\pi int} = \frac{4}{\pi}\sum_{k=0}^{\infty}\frac{1}{2k+1}sin[2\pi (2k+1)t]](http://img.e-com-net.com/image/info8/db96ad670577435489d996669a81ffc2.png)
。
三角波
其本身是连续的但是其导数是不连续的。(事实上，这个导数是方波。) 其Fourier级数是
![\displaystyle \frac{1}{4} +\sum_{k=0}^{\infty}\frac{2}{\pi^{2}(2k+1)^{2}}cos[2\pi (2k+1)t]](http://img.e-com-net.com/image/info8/2dd2a4394928429681a7416bbdff6a99.png)
。
周期函数的平滑度(smoothness)(可微分程度)与收敛速度和Fourier系数的大小密切相关。在前面提到的<
定理 令 f ( t ) 为周期为 1 的周期函数。假设 f ( t ) 是 p 次连续可微的，其中，p 至少为1 。( 这包括在端点 0 和 1 处连续匹配的导数。) 则其部分和
在闭区间[0,1]上随着 N ⟶ ∞ 而逐点且一致地收敛于 f ( t ) 。此外，对于 0 ≤ t ≤1,
。
事实上，在 
的最大值上存在一个趋于 0 的界(随着 N 的增大)。正是这个随着 N 的增大而趋于 0 的界使得这个部分和一致收敛。
我们不证明这个定理；使用来自1.8.1节的 
的 Dirichlet核的表示证明。再一次地，这个结论的一个有趣的方面与函数的局部属性如何反映在其Fourier级数的全局属性中有关。在目前的背景下，函数的“局部属性”是指它的平滑程度，即它连续可导的次数。关于级数，人们可以问的唯一一种“全局问题”是它们收敛的速度有多快，这就是这里的估算值。要点是，近似误差以及间接系数减小的速度是由信号的平滑度(可微分程度)决定的。函数(“局部”表述)越平滑，近似效果就越好，这不仅是平均 L2
意义上的，而且在整个区间(“全局”表述)上都是一致的。此外，Fourier系数本身由积分定义，是函数的全局方面。
关于Fourier系数的可微性和大小的最后评述。平滑度的极端情况是 f ( t )连续可微到任意阶。记录这一点的记法是 f ( t ) 是 [0,1] 上的 
类函数。(这意味着所有导数也在端点处匹配，对于任意 k ≥ 0 ，
。) 在那种情况下，您可以证明，Fourier系数是急速递降的(rapidly decreasing)。这意味着，对于任意 k ≥ 0 ，当 n ⟶±∞ 时，
。
换句话说，比起 n 的任意非负幂，f
(n)更快地趋近于 0 。事实上，反之亦然：如果 Fourier系数是急速递降的,则 f ( t ) 是 [0,1] 上的 类函数。
您可能厌倦了所有这些预示(foreshadowing)，但我们还将看到局部与全局相互作用在Fourier变换的属性中发挥作用，特别是在平滑度(smoothness)和递降率(rate of decay)之间的关系中。这就是为什么我希望我们看到Fourier级数的原因之一。你难道不知道吗：我们还会再次遇到函数急速递降的情况。
1.8.3 复指数真的是L2 ([0,1])的一个正交基吗？(The complex exponentials really are an orthonormal basis for L2 ([0,1] ?)
Fourier级数 理论的热点展示(parade)中剩下的一点是复指数是一个基，即
。
我之前说过，我们不会尝试完整地证明这一点，我们也不会。但通过前面的讨论，我们可以更准确地说明证明是如何进行的，以及我们无法讨论的问题是什么。论证分三步进行。
令 f ( t ) 为一个平方可积函数，并令ε > 0 。
第1步：
中的任意函数都可以用 范数中的一个连续可微函数来逼近。以
的一个已知函数和ε > 0 开始，我们可以求得一个 [0,1] 上的连续可微函数 g(t),使其满足
| f - g| < ε 。
这一步正是我们不能完成的一步！正是在这里，在证明这一表述时，我们需要更一般的Lebesgue积分理论以及随之而来的约束过程(注：事实上， 中的任何函数都可以用无限可微函数来逼近。我们将在第 4 章中以卷积作为平滑运算的背景来讨论这一点)。
第2步：
从上一节的讨论中，我们现在知道连续可微函数(定理表述中的 p = 1)的部分和一致收敛于该函数。因此，对于步骤 1 中的 g(t)，我们可以选择足够大的 N，使得
。
则对于 范数 ，
。
因此，
。
第3步：
请记住，Fourier系数为函数提供了 中的最佳有限逼近。因为我们需要它：
。
则最后
------------------------------------------
------------------------------------------
。
这就证明了
通过取 N 最够大而变得任意小，这就是我们需要做的。
为了使整个图景更加完整，让我添加最后一点，这与我们所做的有点相反。我们不会使用它，但它可以很好地把事情联系起来。
若 
是满足
的任意复数序列，则函数
位于 中，意味着部分和极限收敛于 中的一个函数,并且 
。这通常称为 Riesz-Fischer 定理。
告别这一切。够了吗？有很多材料刚刚经过您的途径，我再说一遍，您可能会在其他场所遇到这些想法和术语。但老实说，这些结果更多的是数学问题，而不是日常实际问题。引用帮助发明快速Fourier变换算法(即将到来的吸引力！)的杰出应用数学家John Tukey的话：“我不想乘坐一架其设计取决于函数是Riemann可积还是Lebesgue可积的飞机。”
1.8.4 附录：逐点收敛对比一致收敛(Appendix: Pointwise convergence vs. uniform convergence)
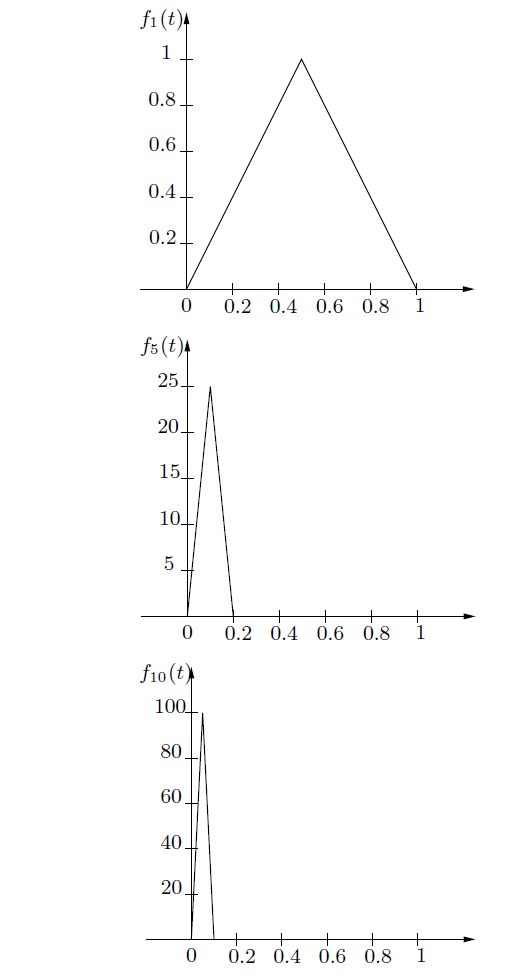
这是一个典型的例子，它表明逐点收敛与一致收敛不同，或者说是同一件事，我们可以拥有一系列函数 
具有这样的属性——当n ⟶ ∞ 时，对于 t 的每一个值，都有 
但是，最终的图像看起来与 f( t)的图像不像。让我们换一句来表述这样一个函数序列，绘一个图，然后让你出它对应的公式。
所有 函数都将定义在[0,1]上。对于每一个 n , 的图像从1/n 到1 都是 零，而对于 0 ≤ t ≤1/n ， 是一个高度为 
的等腰三角形(isosceles triangle)。以下是 
，
，和 
的图像。
-----------------------图 12. ，，和 的图像-----------------------------------
随着 n 的增加，峰值向左滑动并变得越来越高。很明显，对于每个 t，序列 趋于 0 。这是因为对于所有 n，
并且对于任何 t = 0，最终(即，对于足够大的 n)，峰值将逐渐滑到 t 的左侧，并且 从 n 开始将为零。 因此 逐点收敛于常数 0 。但是 的图形肯定不会一致地接近 0！
因为一致收敛非常值得重视，所以您可能会很高兴知道有一个相当灵活的结果可以保证它。它被称为 Weierstrass M检验(Weierstrass M-test)(注：以 K. Weierstrass 的名字命名。他的职业生涯很有趣，主要靠自学成才，并在(德语)高中任教多年。他以强调严谨著称，因此引起了许多数学专业学生和数学教授的无尽担忧)，如下所述。
Weierstrass M检验 令 
为 0 ≤ t ≤1 上的函数的一个序列，并假设存在数 
其具有下列的属性：
(1) 对于每一个固定的 n ,对任意 0 ≤ t ≤1 ，我们有 
。
(2) 数级数 
收敛 。
则，函数级数 
在 0 ≤ t ≤1 上一致收敛。
该定理没有说明级数收敛到什么。
回到第 1.4 节，我们只需要 Weierstrass M检验即可证明三角波的Fourier级数在 0 ≤ t ≤1 时一致收敛。为什么呢？但测试并不能让我们对方波得出任何结论。为什么？
1.9 附录：Cauchy-Schwarz 不等式(Appendix: The Cauchy-Schwarz Inequality)
这是一个著名且有用的不等式。它一定会在某个地方有用，所以就在这里了。Cauchy-Schwarz不等式是两个向量的内积与其范数之间的关系。它指出
。
这是一个真正的主力(workhorse)，你应该知道它。 你甚至会在书中散布的一些问题中看到它的实际应用。
对于几何向量，从内积的几何公式中可以看出这一点很简单，
，
因为 cos(θ) ≤ 1 。实际上，内积几何公式的基本原理(rationale)推导自Cauchy-Schwarz不等式。
如何从几何向量内积的代数定义导出不等式当然并不明显。用分量写出来，不等式表示(对于实数向量)
找个时间坐下来尝试一下。
Cauchy-Schwarz不等式的推导通常仅使用前面列出的内积的四个代数性质。因此，相同的论点适用于满足这些属性的任何乘积，例如 上的内积。这是一个如此优雅的论点(我相信是约John von Neumann提出的)，我想向您证明它。我们将在这里给出真正的内积，并附上对复杂情况的评述。
任何不等式最终都可以用这样的方式来表示：某个数量是正数，或者至少是非负数。 我们所知道的正数的例子有实数的平方、某物的面积和某物的长度。更微妙的不等有时依赖于凸性(convexity)，例如，质量系统的重心包含在质量的凸包 (convex hull)内。这个关于不等本质的小小即兴表演(riff)可以说是宇宙的一个小秘密。
为了证明Cauchy-Schwarz不等式，我们使用向量的范数是非负的，但我们引入一个参数。令 r 为任意实数。则 
。将其写为内积并使用代数性质进行扩展；由于同质性、对称性和可加性，这就像乘法一样——认识到这一点很重要：
。
这是 r 为未知数的二次方程，形如 
，其中 
，
，
。第一个不等式以及随后的一系列(the chain of)等式表明，这个二次方程始终是非负的。现在，始终为非负的二次方程必须具有非正判别式(discriminant):判别式 确定了这个二次方程的根的特征，如果判别式为正，则有两个实根，如果有两个实根，则二次方一定在某处为负。因此，
,转换成
或者 
。
不等式两边取平方根，得到
，
如预期结果。很惊奇，不是吗——二次公式的重要应用(注：作为这个论点的一个小替代，如果这个二次方程处处非负，则，特别地，其最小值是非负。最小值发生在 t = -b/(2a)，最终导出同样的不等式 
)。
回到几何，我们现在知道
。
因此，存在唯一的一个角 θ (0 ≤ θ ≤π)，使得
。
即 ， 
。
这也证明了Cauchy-Schwarz不等式中等式何时成立，即向量方向相同(或相反)的情况。
三角不等式
可以从Cauchy-Schwarz不等式直接导出。下面是论证。
---------------
---------------
---------------
(根据Cauchy-Schwarz不等式)
--------------
--------------
。
对上式两边取平方根，得到 。在坐标中，它表明
。
以下是如何从我们已经完成的工作中获得复数内积的Cauchy-Schwarz不等式。对于复数向量
和 
，不等式表明
。
在不等式的左边，我们有复数 
的大小。与我们在现实情况中所做的略有不同，令 
为一个复数(r是实数)，并考虑
-------------------------
-------------------------
。
现在，我们可以选择 θ 为我们想要的任何值，这样做是为了使
。
用 
乘以 将复数 顺时针方向旋转θ角,因此，选择 θ 以将 旋转到实数轴和正数。从这里开始，论证与现实情况中的论证是一样的。
1.9.1 L2 ([0,1] 的Cauchy-Schwarz 不等式(Cauchy-Schwarz for L2 ([0,1])
让我再次强调，Cauchy-Schwarz不等式的证明仅取决于内积的代数性质，因此对于 上的(复)内积成立。 它采用令人印象深刻的形式
。
我们现在还知道三角不等式成立：
|f + g| ≤ || f || + || g|| ，
即，
。
顺便说一句，内积确实有意义。 由于这是数学部分，我应该指出我跳过了数学部分。如果 f (t) 和 f (t) 是平方可积的，那么为了使Cauchy-Schwarz不等式成立，必须知道内积 (f, g) 有意义，即
。
不用恐惧，要推断出这一点，您可以使用
。
这是算术平均值和几何平均值之间的不等式——查一下(注：又是正的：
) 则
------------------------
。
因为我们以假设 f (t) 和 f (t) 是平方可积的开始。Cauchy-Schwarz不等式是有根据的，我们很高兴。
1.9.2 Fourier系数适用Cauchy-Schwarz不等式很好(The Fourier coefficients are fine)
现在我们知道Cauchy-Schwarz不等式确实没问题，一个结果是幸运的事实是中函数的Fourier系数存在。也就是说，我们可能想知道是否存在
。
我们不用考虑太多(注：您还可以通过使用算术几何平均不等式来推断 
有意义)：
。
1.9.3 卷积也适用Cauchy-Schwarz不等式(And convolution is also OK)
我们并没有提出确定两个周期函数 f (t)，g (t)的卷积 (f * g)( t) 是否确实被定义的问题，即积分
存在。
假设 f (t)，g (t) 是 函数，我们有
。
现在您可以通过调用周期性来完成右侧有限的论证：
。
1.9.4 平方可积意味着可积(Square integrable implies integrable)
Cauchy-Schwarz的另一个有时被低估的结论是，平方可积函数也是绝对可积的，这意味着如果
，
则，
。
为了理论这一点，应用 Cauchy-Schwarz 不等式到 | f (t)|.1 ，产生
，
因为 f (t) 和 常量函数 1 在闭区间 [0，1]上都是平方可积的。
忠告：
如果闭区间 [0, 1] 被整条实数轴替换，这个简单的、几乎是随手的论证就“无效了”。 常数函数 1 在 ℝ 上有一个无限积分。您可能认为我们可以解决这个小不便，但这“正是”在尝试将Fourier “级数”思想(其中函数在有限间隔上定义)应用到Fourier变换的想法(其中函数在所有 ℝ 上都有定义) 时有时会出现的麻烦。
内容来源：
<
参考资料：
<
<< Fourier Analysis for Beginners>> Larry N. Thibos
<