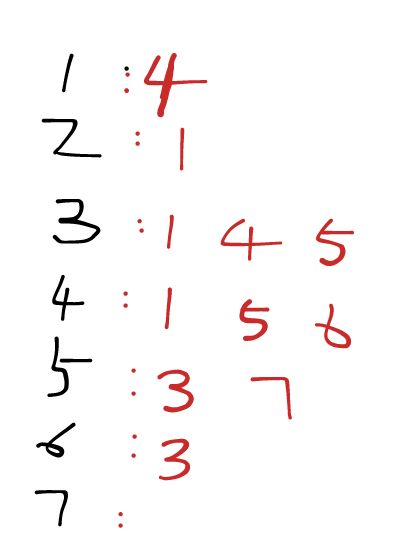bfs与dfs详解（经典例题 + 模板c-代码）

文章首发于：My Blog 欢迎大佬们前来逛逛

模板+解析

DFS（深度优先搜索）和BFS（广度优先搜索）是图论中两个重要的算法。

dfs

其中DFS是一种用于遍历或搜索树或图的算法，BFS则是一种用于搜索或遍历树或图的算法。两种算法都有其自身的优点和缺点，应用于不同的场景中。 DFS（深度优先搜索） 深度优先搜索是一种用于遍历或搜索树或图的算法，其基本思路是从起始节点开始，沿着一条路径一直走到底，直到无法再走下去为止，然后回溯到上一个节点，继续走到另外一个路径，重复上述过程，直到遍历完所有节点。

DFS的实现方式可以采用递归或者栈来实现。下面是一个采用递归方式实现的DFS代码示例（C++）：

void dfs(int cur, vector<int>& visited, vector<vector<int>>& graph) {
    visited[cur] = 1; // 标记当前节点已经被访问
    // 处理当前节点cur
    for (int i = 0; i < graph[cur].size(); i++) {
        int next = graph[cur][i];
        if (!visited[next]) { // 如果下一个节点未被访问
            dfs(next, visited, graph); // 继续访问下一个节点
        }
    }
}
void dfsTraversal(vector<vector<int>>& graph) {
    int n = graph.size();
    vector<int> visited(n, 0); // 初始化访问数组
    for (int i = 0; i < n; i++) {
        if (!visited[i]) { // 如果当前节点未被访问
            dfs(i, visited, graph); // 从当前节点开始进行深度优先遍历
        }
    }
}

bfs

BFS（广度优先搜索） 广度优先搜索是一种用于搜索或遍历树或图的算法，其基本思路是从起始节点开始，依次遍历当前节点的所有邻居节点，然后再依次遍历邻居节点的所有邻居节点，直到遍历到目标节点或者遍历完所有节点。 BFS的实现方式可以采用队列来实现。下面是一个采用队列方式实现的BFS代码示例（C++）：

void bfsTraversal(vector<vector<int>>& graph) {
    int n = graph.size();
    vector<int> visited(n, 0); // 初始化访问数组
    queue<int> q;
    for (int i = 0; i < n; i++) {
        if (!visited[i]) { // 如果当前节点未被访问
            q.push(i); // 将当前节点加入队列
            visited[i] = 1; // 标记当前节点已经被访问
            while (!q.empty()) { // 循环遍历队列中的节点
                int cur = q.front();
                q.pop();
                // 处理当前节点cur
                for (int j = 0; j < graph[cur].size(); j++) {
                    int next = graph[cur][j];
                    if (!visited[next]) { // 如果下一个节点未被访问
                        q.push(next); // 将下一个节点加入队列
                        visited[next] = 1; // 标记下一个节点已经被访问
                    }
                }
            }
        }
    }
}

总结 DFS和BFS都是图论中常用的搜索算法，其应用广泛，例如在寻路、迷宫问题、拓扑排序、连通性等问题中都有应用。两种算法的实现方式不同，DFS采用递归或者栈实现，而BFS采用队列实现。在应用场景中，需要根据实际情况选择合适的算法来解决问题。

---

1562. 微博转发

1562. 微博转发

题目要求：有n个人，每个人都有关注的人和粉丝，如果某一个人发了一条微博，则他的粉丝们都会进行转发，而他的粉丝又会被他的粉丝的粉丝转发，求出在 L层关注者的前提下，微博转发数量的最大值。

---

我们可以观察到每个明星都有粉丝，则这些粉丝就是他们的孩子们，我们把这个明星看作是树的根节点，因此题目要求就是让我们求 从根节点出发在k层以内的不同的孩子节点的个数。

注意到题目输入的是 **某一个人关注了这个明星。**是一个从孩子节点到根节点的路径

我们可以把这个路径反过来，写成：谁的粉丝有谁。

这样我们就可以转换成一个树结构，从根节点出发在k层内的孩子的个数。

转换的关系如下所示，表示 x节点的孩子是 n1,n2…

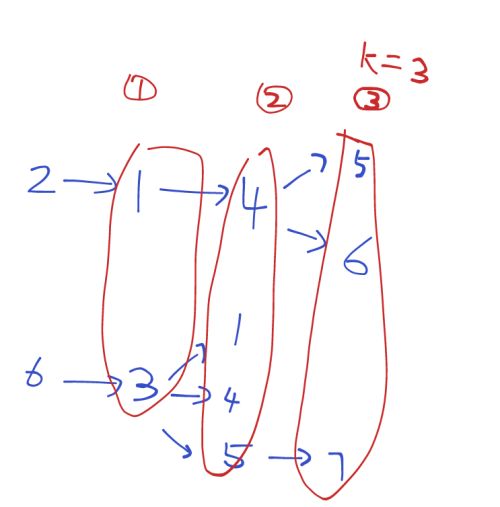
然后利用bfs求得在k层内的最大的数量，其中对于k层的约束我们可以使用一个步数来进行表示，如果步数超过了k步，则直接退出；否则记录孩子的数量，同时进入孩子节点，重新开始bfs。

最后经过了bfs后，我们得到的一定k层以内最全的孩子的数量。

我们可以使用邻接矩阵表示他们的关系，可以使用vector容器，也可以自己实现一个链式前向星存图，不过：

vector容器耗时： 1339 ms

链式前向星：388 ms

Ac代码如下：

#include 
using namespace std;
const int N=1010;
typedef pair<int,int> PI;
vector<int> vec[N];
int n,k;
set<int> st;
bool vis[N];
/* 链式前向星
struct Edge{
    int to,next;
}edge[N];
int head[N],cnt;
bool vis[N];
void add_edge(int u,int v){
    edge[++cnt].to=v;
    edge[cnt].next=head[u];
    head[u]=cnt;
}
*/
int bfs(int s){
    st.clear();
    queue<PI> q;
    q.push({0,s});
    vis[s]=true;
    bool fg=false;
    while (!q.empty()){
        auto p=q.front();
        q.pop();
        int u=p.second;//当前点
        for (auto& x:vec[u]){//x表示当前点的所有孩子
            if (!vis[x]){
                if (p.first+1>k){//超过了k层
                    fg=true;
                    break;
                }
                vis[x]=true;
                st.insert(x);
                q.push({p.first+1,x});
            }
        }
        if (fg) break;
    }
    return st.size();
}
int main(){
    cin>>n>>k;
    for (int i=1;i<=n;i++){
        int x;
        cin>>x;
        while( x--){
            //num的粉丝是i
            int num;
            cin>>num;
            vec[num].push_back(i);
        }
    }
    cin>>n;
    while (n--){
        memset(vis,0,sizeof(vis));
        int num;
        cin>>num;
        cout<<bfs(num)<<'\n';
    }
    return 0;
}

---

3502. 不同路径数

3502. 不同路径数

题目要求：在一个n*m的矩阵中，每走一步可以添加一个数字，最终走完k步，一共可以构成多少个不同的数字？

n和m的数据范围非常小，最大只有5，而且k也很小，因此我们随便造就完了

很明显我们使用深搜。直接暴力搜索所有的数字即可，然后存在一个set中，最后返回set的元素数量。

#include 
using namespace std;
const int N=10;
int n,m,k;
int nums[N][N];
set<int> st;
int dx[4]={-1,1,0,0},dy[4]={0,0,-1,1};
void dfs(int x,int y,int sum,int step){
    if (step>=k){
        //如果步数超限，则记录这个数字
        st.insert(sum);
        return;
    }
    for (int i=0;i<4;i++){
        int cx=x+dx[i],cy=y+dy[i];
        if (cx>=1 && cx<=n && cy>=1 && cy<=m){
            dfs(cx,cy,sum*10+nums[cx][cy],step+1);  //步数+1
            //更新当前的sum总和=sum*10+nums[cx][cy]）(秦九韶算法)
        }
    }
}
int main(){
    cin>>n>>m>>k;
    for (int i=1;i<=n;i++){
        for (int j=1;j<=m;j++){
            cin>>nums[i][j];
        }
    }
    for (int i=1;i<=n;i++){
        for (int j=1;j<=m;j++){
            //直接全部遍历不解释
            dfs(i,j,nums[i][j],0);
        }
    }
    cout<<st.size();
    return 0;
}

---

165. 小猫爬山

165. 小猫爬山

题目要求：有n个物品，每几个物品之间都可以放在一辆车上，前提是这几件物品的重量不能超过车的最大承受重量，每一辆车一美元，求得最少需要支付多少美元，才能运完这些全部的物品。

---

一看到这道题貌似就能看出可以用贪心来做。

即按照从大到小或者从小到大排序，然后如果超过了重量则新增一辆车。

但是！！贪心并不是最优的选择。为什么呢？

就像换硬币一样，我们贪心并不能得到最优的选择，动态规划才是最后的选择（我忘记哪道题了，有知道的大佬可以评论区回复我以下）

---

因此我们选择深搜，并且这道题也是非常经典的一类深搜问题。

遍历所有的物品：

• 如果当前物品可以放入这辆车，则放入这辆车，车辆总数不变，但是物品编号+1，表示开始下一个物品
• 如果当前物品不能放入这辆车，则需要新增加一辆车，而且物品编号也要+1.
• 每一个物品可以选择放入这辆车，也可以选择不放入，因此需要进行回溯
• 剪枝：如果当前车辆数量超过了答案，则一定不是最优解
• 当 最后一个物品也成功放入后，即 now-1==n ，则全部物品都放入，则记录答案。

#include 
using namespace std;
const int N=20;
int nums[N]; //每个物品的重量
int n,k;
int cnt;//车的总数量
int car[N]; //所有的车的载物情况
int ans=99999999;
void dfs(int now,int c){
    //now：当前物品
    //c：当前的车辆编号
    
    //剪枝
    if (c>=ans){
        //如果c超过了ans，则一定不是最优解
        return;
    }
    if (now-1==n){
        //所有的物品都遍历过了，则记录一个cnt数量
        ans=min(ans,c);
        return;
    }
    for (int i=1;i<=c;i++){//遍历所有的已经存在的车
        if (nums[now]+car[i]<=k){
            //now物品可以放在编号为i的这辆车上
            car[i]+=nums[now];
            dfs(now+1,c); //下一个物品，仍是当前车
            car[i]-=nums[now];//回溯
        }
    }
    //如果所有的物品都不能放在now这辆车上，则新增一辆车
    car[c+1]+=nums[now];
    dfs(now+1,c+1); //下一个物品，新增一辆车
    car[c+1]-=nums[now];//回溯
}
int main(){
    cin>>n>>k;//k是车最大承重 
    for (int i=1;i<=n;i++){
        cin>>nums[i];
    }
    dfs(1,0); 
    cout<<ans;
    
    return 0;
}