【Python机器学习】实验10 支持向量机

文章目录

支持向量机
- 实例1 线性可分的支持向量机
- - 1.1 数据读取
  - 1.2 准备训练数据
  - 1.3 实例化线性支持向量机
  - 1.4 可视化分析
- 实例2 核支持向量机
- - 2.1 读取数据集
  - 2.2 定义高斯核函数
  - 2.3 创建非线性的支持向量机
  - 2.4 可视化样本类别
- 实例3 如何选择最优的C和gamma
- - 3.1 读取数据
  - 3.2 利用数据集中的验证集做模型选择
- 实例4 基于鸢尾花数据集的决策边界绘制
- - 4.1 读取鸢尾花数据集（特征选择花萼长度和花萼宽度）
  - 4.2 随机绘制几条决策边界可视化
  - 4.3 随机绘制几条决策边界可视化
  - 4.4 最大间隔决策边界可视化
- 实例5 特征是否应该进行标准化？
- - 5.1 原始特征的决策边界可视化
  - 5.1 标准化特征的决策边界可视化
- 实例6
- 实例7 非线性可分的决策边界
- - 7.1 做一个新的数据
  - 7.2 绘制高高线表示预测结果
  - 7.3 绘制原始数据
  - 7.4 绘制不同gamma和C对应的
- 实例8* 手写SVM
- - 8.1 创建数据
  - 8.2 定义支持向量机
  - 8.3 初始化支持向量机并拟合
  - 8.4 支持向量机得到分数
- 实验1 采用以下数据作为数据集，分别基于线性和核支持向量机进行分类，对于线性核绘制决策边界
- - 1 获取数据
  - 2 可视化数据
  - 3 试试采用线性支持向量机来拟合
  - 4 试试采用核支持向量机
  - 5 绘制线性支持向量机的决策边界
  - 6 绘制非线性决策边界

支持向量机

在本练习中，我们将使用支持向量机（SVM）来构建垃圾邮件分类器。我们将从一些简单的2D数据集开始使用SVM来查看它们的工作原理。然后，我们将对一组原始电子邮件进行一些预处理工作，并使用SVM在处理的电子邮件上构建分类器，以确定它们是否为垃圾邮件。

我们要做的第一件事是看一个简单的二维数据集，看看线性SVM如何对数据集进行不同的C值（类似于线性/逻辑回归中的正则化项）。

实例1 线性可分的支持向量机

1.1 数据读取

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb

import warnings
warnings.simplefilter("ignore")

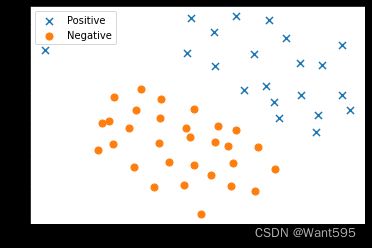
我们将其用散点图表示，其中类标签由符号表示（+表示正类，o表示负类）。

data1 = pd.read_csv('data/svmdata1.csv')

data1.head()

	X1	X2	y
0	1.9643	4.5957	1
1	2.2753	3.8589	1
2	2.9781	4.5651	1
3	2.9320	3.5519	1
4	3.5772	2.8560	1

positive=data1[data1["y"].isin([1])]
negative=data1[data1["y"].isin([0])]
negative

	X1	X2
20	1.58410	3.3575
21	2.01030	3.2039
22	1.95270	2.7843
23	2.27530	2.7127
24	2.30990	2.9584
25	2.82830	2.6309
26	3.04730	2.2931
27	2.48270	2.0373
28	2.50570	2.3853
29	1.87210	2.0577
30	2.01030	2.3546
31	1.22690	2.3239
32	1.89510	2.9174
33	1.56100	3.0709
34	1.54950	2.6923
35	1.68780	2.4057
36	1.49190	2.0271
37	0.96200	2.6820
38	1.16930	2.9276
39	0.81220	2.9992
40	0.97350	3.3881
41	1.25000	3.1937
42	1.31910	3.5109
43	2.22920	2.2010
44	2.44820	2.6411
45	2.79380	1.9656
46	2.09100	1.6177
47	2.54030	2.8867
48	0.90440	3.0198
49	0.76615	2.5899

positive = data1[data1['y'].isin([1])]
negative = data1[data1['y'].isin([0])]
fig, ax = plt.subplots(figsize=(6,4))
ax.scatter(positive['X1'], positive['X2'], s=50, marker='x', label='Positive')
ax.scatter(negative['X1'], negative['X2'], s=50, marker='o', label='Negative')
ax.legend()
plt.show()

请注意，还有一个异常的正例在其他样本之外。
这些类仍然是线性分离的，但它非常紧凑。我们要训练线性支持向量机来学习类边界。在这个练习中，我们没有从头开始执行SVM的任务，所以用scikit-learn。

1.2 准备训练数据

在这里，我们不准备测试数据，直接用所有数据训练，然后查看训练完成后，每个点属于这个类别的置信度

X_train=data1[["X1","X2"]].values

y_train=data1["y"].values

1.3 实例化线性支持向量机

#建立第一个支持向量机对象,C=1
from sklearn import svm
svc1=svm.LinearSVC(C=1,loss="hinge",max_iter=1000)
svc1.fit(X_train,y_train)
svc1.score(X_train,y_train)

0.9803921568627451

from sklearn.model_selection import cross_val_score
cross_val_score(svc1,X_train,y_train,cv=5).mean()

0.9800000000000001

让我们看看如果C的值越大，会发生什么

#建立第二个支持向量机对象C=100
svc2=svm.LinearSVC(C=100,loss="hinge",max_iter=1000)
svc2.fit(X_train,y_train)
svc2.score(X_train,y_train)

0.9411764705882353

from sklearn.model_selection import cross_val_score
cross_val_score(svc2,X_train,y_train,cv=5).mean()

0.96

X_train.shape

(51, 2)

svc1.decision_function(X_train).shape

(51,)

#建立两个支持向量机的决策函数
data1["SV1 decision function"]=svc1.decision_function(X_train)
data1["SV2 decision function"]=svc2.decision_function(X_train)

data1

	X1	X2	y	SV1 decision function	SV2 decision function
0	1.964300	4.5957	1	0.798413	4.490754
1	2.275300	3.8589	1	0.380809	2.544578
2	2.978100	4.5651	1	1.373025	5.668147
3	2.932000	3.5519	1	0.518562	2.396315
4	3.577200	2.8560	1	0.332007	1.000000
5	4.015000	3.1937	1	0.866642	2.621549
6	3.381400	3.4291	1	0.684095	2.571736
7	3.911300	4.1761	1	1.607362	5.607368
8	2.782200	4.0431	1	0.830991	3.766091
9	2.551800	4.6162	1	1.162616	5.294331
10	3.369800	3.9101	1	1.069933	4.082890
11	3.104800	3.0709	1	0.228063	1.087807
12	1.918200	4.0534	1	0.328403	2.712621
13	2.263800	4.3706	1	0.791771	4.153238
14	2.655500	3.5008	1	0.313312	1.886635
15	3.185500	4.2888	1	1.270111	5.052445
16	3.657900	3.8692	1	1.206933	4.315328
17	3.911300	3.4291	1	0.997496	3.237878
18	3.600200	3.1221	1	0.562860	1.872985
19	3.035700	3.3165	1	0.387708	1.779986
20	1.584100	3.3575	0	-0.437342	0.085220
21	2.010300	3.2039	0	-0.310676	0.133779
22	1.952700	2.7843	0	-0.687313	-1.269605
23	2.275300	2.7127	0	-0.554972	-1.091178
24	2.309900	2.9584	0	-0.333914	-0.268319
25	2.828300	2.6309	0	-0.294693	-0.655467
26	3.047300	2.2931	0	-0.440957	-1.451665
27	2.482700	2.0373	0	-0.983720	-2.972828
28	2.505700	2.3853	0	-0.686002	-1.840056
29	1.872100	2.0577	0	-1.328194	-3.675710
30	2.010300	2.3546	0	-1.004062	-2.560208
31	1.226900	2.3239	0	-1.492455	-3.642407
32	1.895100	2.9174	0	-0.612714	-0.919820
33	1.561000	3.0709	0	-0.684991	-0.852917
34	1.549500	2.6923	0	-1.000889	-2.068296
35	1.687800	2.4057	0	-1.153080	-2.803536
36	1.491900	2.0271	0	-1.578039	-4.250726
37	0.962000	2.6820	0	-1.356765	-2.839519
38	1.169300	2.9276	0	-1.033648	-1.799875
39	0.812200	2.9992	0	-1.186393	-2.021672
40	0.973500	3.3881	0	-0.773489	-0.585307
41	1.250000	3.1937	0	-0.768670	-0.854355
42	1.319100	3.5109	0	-0.468833	0.238673
43	2.229200	2.2010	0	-1.000000	-2.772247
44	2.448200	2.6411	0	-0.511169	-1.100940
45	2.793800	1.9656	0	-0.858263	-2.809175
46	2.091000	1.6177	0	-1.557954	-4.796212
47	2.540300	2.8867	0	-0.256185	-0.206115
48	0.904400	3.0198	0	-1.115044	-1.840424
49	0.766150	2.5899	0	-1.547789	-3.377865
50	0.086405	4.1045	1	-0.713261	0.571946

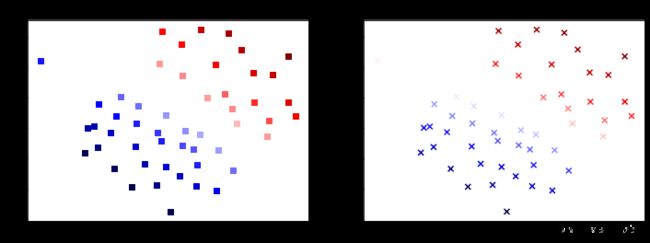
采用决策函数的值作为颜色来看看每个点的置信度，比较两个支持向量机产生的结果的差异

1.4 可视化分析

#绘制图片
plt.figure(figsize=(12,4))
plt.subplot(1,2,1)
plt.scatter(data1["X1"],data1["X2"],marker="s",c=data1["SV1 decision function"],cmap='seismic')
plt.title("SVC1")
plt.subplot(1,2,2)
plt.scatter(data1["X1"],data1["X2"],marker="x",c=data1["SV2 decision function"],cmap='seismic')
plt.title("SVC2")
plt.show()

实例2 核支持向量机

现在我们将从线性SVM转移到能够使用内核进行非线性分类的SVM。我们首先负责实现一个高斯核函数。虽然scikit-learn具有内置的高斯内核，但为了实现更清楚，我们将从头开始实现。

2.1 读取数据集

data2 = pd.read_csv('data/svmdata2.csv')
data2

	X1	X2	y
0	0.107143	0.603070	1
1	0.093318	0.649854	1
2	0.097926	0.705409	1
3	0.155530	0.784357	1
4	0.210829	0.866228	1
...	...	...	...
858	0.994240	0.516667	1
859	0.964286	0.472807	1
860	0.975806	0.439474	1
861	0.989631	0.425439	1
862	0.996544	0.414912	1

863 rows × 3 columns

#可视化数据点
positive = data2[data2['y'].isin([1])]
negative = data2[data2['y'].isin([0])]
fig, ax = plt.subplots(figsize=(6,4))
ax.scatter(positive['X1'], positive['X2'], s=50, marker='x', label='Positive')
ax.scatter(negative['X1'], negative['X2'], s=50, marker='o', label='Negative')
ax.legend()
plt.show()

2.2 定义高斯核函数

def gaussian(x1,x2,sigma):
    return np.exp(-np.sum((x1-x2)**2)/(2*(sigma**2)))

x1=np.arange(1,5)
x2=np.arange(6,10)
gaussian(x1,x2,2)

3.726653172078671e-06

x1 = np.array([1.0, 2.0, 1.0])
x2 = np.array([0.0, 4.0, -1.0])
sigma = 2
gaussian(x1,x2,2)

0.32465246735834974

X2_train=data2[["X1","X2"]].values
y2_train=data2["y"].values
X2_train,y2_train

(array([[0.107143 , 0.60307  ],
        [0.093318 , 0.649854 ],
        [0.0979263, 0.705409 ],
        ...,
        [0.975806 , 0.439474 ],
        [0.989631 , 0.425439 ],
        [0.996544 , 0.414912 ]]),
 array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1], dtype=int64))

该结果与练习中的预期值相符。接下来，我们将检查另一个数据集，这次用非线性决策边界。

对于该数据集，我们将使用内置的RBF内核构建支持向量机分类器，并检查其对训练数据的准确性。为了可视化决策边界，这一次我们将根据实例具有负类标签的预测概率来对点做阴影。从结果可以看出，它们大部分是正确的。

2.3 创建非线性的支持向量机

import sklearn.svm as svm
nl_svc=svm.SVC(C=100,gamma=10,probability=True)
nl_svc.fit(X2_train,y2_train)

SVC(C=100, gamma=10, probability=True)

nl_svc.score(X2_train,y2_train)

0.9698725376593279

2.4 可视化样本类别

#将样本属于正类的概率作为颜色来对两类样本进行可视化输出
plt.figure(figsize=(12,4))
plt.subplot(1,2,1)
positive = data2[data2['y'].isin([1])]
negative = data2[data2['y'].isin([0])]
plt.scatter(positive['X1'], positive['X2'], s=50, marker='x', label='Positive')
plt.scatter(negative['X1'], negative['X2'], s=50, marker='o', label='Negative')
plt.legend()
plt.subplot(1,2,2)
data2["probability"]=nl_svc.predict_proba(data2[["X1","X2"]])[:,1]
plt.scatter(data2["X1"],data2["X2"],s=30,c=data2["probability"],cmap="Reds")
plt.show()

对于第三个数据集，我们给出了训练和验证集，并且基于验证集性能为SVM模型找到最优超参数。虽然我们可以使用scikit-learn的内置网格搜索来做到这一点，但是本着遵循练习的目的，我们将从头开始实现一个简单的网格搜索。

实例3 如何选择最优的C和gamma

3.1 读取数据

#读取文件，获取数据集
data3=pd.read_csv('data/svmdata3.csv')
#读取文件，获取验证集
data3val=pd.read_csv('data/svmdata3val.csv')

data3

	X1	X2	y
0	-0.158986	0.423977	1
1	-0.347926	0.470760	1
2	-0.504608	0.353801	1
3	-0.596774	0.114035	1
4	-0.518433	-0.172515	1
...	...	...	...
206	-0.399885	-0.621930	1
207	-0.124078	-0.126608	1
208	-0.316935	-0.228947	1
209	-0.294124	-0.134795	0
210	-0.153111	0.184503	0

211 rows × 3 columns

data3val

	X1	X2	yval	y
0	-0.353062	-0.673902	0	0
1	-0.227126	0.447320	1	1
2	0.092898	-0.753524	0	0
3	0.148243	-0.718473	0	0
4	-0.001512	0.162928	0	0
...	...	...	...	...
195	0.005203	-0.544449	1	1
196	0.176352	-0.572454	0	0
197	0.127651	-0.340938	0	0
198	0.248682	-0.497502	0	0
199	-0.316899	-0.429413	0	0

200 rows × 4 columns

X = data3[['X1','X2']].values
Xval = data3val[['X1','X2']].values
y = data3['y'].values
yval = data3val['yval'].values

3.2 利用数据集中的验证集做模型选择

C_values = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]
gamma_values = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]

best_score = 0
best_params = {'C': None, 'gamma': None}

for C in C_values:
    for gamma in gamma_values:
        svc = svm.SVC(C=C, gamma=gamma)
        svc.fit(X, y)
        score = svc.score(Xval, yval)
        if score > best_score:
            best_score = score
            best_params['C'] = C
            best_params['gamma'] = gamma
best_score, best_params

(0.965, {'C': 0.3, 'gamma': 100})

from sklearn import svm, datasets
from sklearn.model_selection import GridSearchCV
parameters = {'gamma':[0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100], 'C': [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]}
svc = svm.SVC()
clf = GridSearchCV(svc, parameters)
clf.fit(X, y)
# sorted(clf.cv_results_.keys())
max_index=np.argmax(clf.cv_results_['mean_test_score'])

clf.cv_results_["params"][max_index]

{'C': 30, 'gamma': 3}

实例4 基于鸢尾花数据集的决策边界绘制

4.1 读取鸢尾花数据集（特征选择花萼长度和花萼宽度）

from sklearn.svm import SVC
from sklearn import datasets
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]  # petal length, petal width
y = iris["target"]

setosa_or_versicolor = (y == 0) | (y == 1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]

# SVM Classifier model
svm_clf = SVC(kernel="linear", C=5)
svm_clf.fit(X, y)

SVC(C=5, kernel='linear')

np.max(X[:,0])

5.1

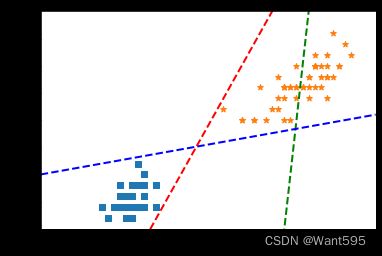
4.2 随机绘制几条决策边界可视化

# Bad models
x0 = np.linspace(0, 5.5, 200)
pred_1 = 5 * x0 - 20
pred_2 = x0 - 1.8
pred_3 = 0.1 * x0 + 0.5

#基于随机绘制的决策边界来叠加图
plt.figure(figsize=(6,4))
plt.plot(x0, pred_1, "g--", linewidth=2)
plt.plot(x0, pred_2, "r--", linewidth=2)
plt.plot(x0, pred_3, "b--", linewidth=2)
plt.scatter(X[:,0][y==0],X[:,1][y==0],marker="s")
plt.scatter(X[:,0][y==1],X[:,1][y==1],marker="*")
plt.axis([0, 5.5, 0, 2])
plt.show()
plt.show()

4.3 随机绘制几条决策边界可视化

svm_clf.coef_[0]

array([1.29411744, 0.82352928])

svm_clf.intercept_[0]

-3.7882347112962464

svm_clf.support_vectors_

array([[1.9, 0.4],
       [3. , 1.1]])

np.max(X[:,0]),np.min(X[:,0])

(5.1, 1.0)

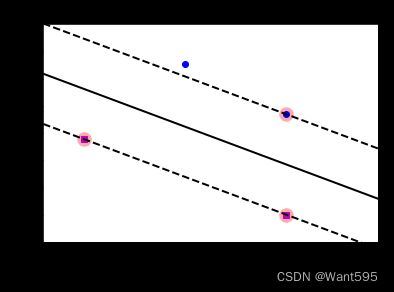
4.4 最大间隔决策边界可视化

def plot_svc_decision_boundary(svm_clf, xmin, xmax):
    
    w = svm_clf.coef_[0]
    b = svm_clf.intercept_[0]

    # At the decision boundary, w0*x0 + w1*x1 + b = 0
    # => x1 = -w0/w1 * x0 - b/w1
    x0 = np.linspace(xmin, xmax, 200)
    decision_boundary = -w[0]/w[1] * x0 - b/w[1]

    # margin = 1/np.sqrt(w[1]**2+w[0]**2)
    margin = 1/0.9
    
    margin = 1/w[1]
    
    gutter_up = decision_boundary + margin
    gutter_down = decision_boundary - margin

    svs = svm_clf.support_vectors_
    plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#FFAAAA')
    plt.plot(x0, decision_boundary, "k-", linewidth=2)
    plt.plot(x0, gutter_up, "k--", linewidth=2)
    plt.plot(x0, gutter_down, "k--", linewidth=2)

plt.figure(figsize=(6,4))
plot_svc_decision_boundary(svm_clf, 0, 5.5)
plt.plot(X[:, 0][y == 1], X[:, 1][y == 1], "bs")
plt.plot(X[:, 0][y == 0], X[:, 1][y == 0], "yo")
plt.xlabel("Petal length", fontsize=14)
plt.axis([0, 5.5, 0, 2])

plt.show()

实例5 特征是否应该进行标准化？

5.1 原始特征的决策边界可视化

#准备数据
Xs = np.array([[1, 50], [5, 20], [3, 80], [5, 60]]).astype(np.float64)
ys = np.array([0, 0, 1, 1])
#实例化模型
svm_clf = SVC(kernel="linear", C=100)
svm_clf.fit(Xs, ys)
#绘制图形
plt.figure(figsize=(6,4))
plt.plot(Xs[:, 0][ys == 1], Xs[:, 1][ys == 1], "bo")
plt.plot(Xs[:, 0][ys == 0], Xs[:, 1][ys == 0], "ms")
plot_svc_decision_boundary(svm_clf, 0, 6)
plt.xlabel("$x_0$", fontsize=20)
plt.ylabel("$x_1$  ", fontsize=20, rotation=0)
plt.title("Unscaled", fontsize=16)
plt.axis([0, 6, 0, 90])

(0.0, 6.0, 0.0, 90.0)

5.1 标准化特征的决策边界可视化

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(Xs)
svm_clf.fit(X_scaled, ys)
plt.plot(X_scaled[:, 0][ys == 1], X_scaled[:, 1][ys == 1], "bo")
plt.plot(X_scaled[:, 0][ys == 0], X_scaled[:, 1][ys == 0], "ms")
plot_svc_decision_boundary(svm_clf, -2, 2)
plt.xlabel("$x_0$", fontsize=20)
plt.title("Scaled", fontsize=16)
plt.axis([-2, 2, -2, 2])
plt.show()

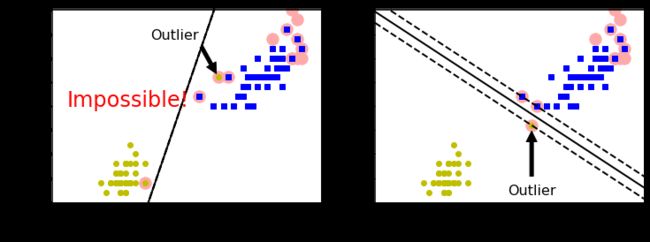
实例6

#回到鸢尾花数据集
X = iris["data"][:, (2, 3)]  # petal length, petal width
y = iris["target"]

X_outliers = np.array([[3.4, 1.3], [3.2, 0.8]])
y_outliers = np.array([0, 0])

Xo1 = np.concatenate([X, X_outliers[:1]], axis=0)
yo1 = np.concatenate([y, y_outliers[:1]], axis=0)
Xo2 = np.concatenate([X, X_outliers[1:]], axis=0)
yo2 = np.concatenate([y, y_outliers[1:]], axis=0)

svm_clf1= SVC(kernel="linear", C=10**9)
svm_clf1.fit(Xo1, yo1)


plt.figure(figsize=(12, 4))

plt.subplot(121)
plt.plot(Xo1[:, 0][yo1 == 1], Xo1[:, 1][yo1 == 1], "bs")
plt.plot(Xo1[:, 0][yo1 == 0], Xo1[:, 1][yo1 == 0], "yo")
plt.text(0.3, 1.0, "Impossible!", fontsize=24, color="red")
plot_svc_decision_boundary(svm_clf1, 0, 5.5)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.annotate(
    "Outlier",
    xy=(X_outliers[0][0], X_outliers[0][1]),
    xytext=(2.5, 1.7),
    ha="center",
    arrowprops=dict(facecolor='black', shrink=0.1),
    fontsize=16,
)
plt.axis([0, 5.5, 0, 2])


svm_clf2 = SVC(kernel="linear", C=10**9)
svm_clf2.fit(Xo2, yo2)

plt.subplot(122)
plt.plot(Xo2[:, 0][yo2 == 1], Xo2[:, 1][yo2 == 1], "bs")
plt.plot(Xo2[:, 0][yo2 == 0], Xo2[:, 1][yo2 == 0], "yo")
plot_svc_decision_boundary(svm_clf2, 0, 5.5)
plt.xlabel("Petal length", fontsize=14)
plt.annotate(
    "Outlier",
    xy=(X_outliers[1][0], X_outliers[1][1]),
    xytext=(3.2, 0.08),
    ha="center",
    arrowprops=dict(facecolor='black', shrink=0.1),
    fontsize=16,
)
plt.axis([0, 5.5, 0, 2])

plt.show()
plt.show()

实例7 非线性可分的决策边界

7.1 做一个新的数据

from sklearn.pipeline import Pipeline

from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)

np.min(X[:,0]),np.max(X[:,0])

(-1.2720155884887554, 2.4093807207967215)

np.min(X[:,1]),np.max(X[:,1])

(-0.6491427462708279, 1.2711135917248466)

x0s = np.linspace(2, 15, 2)
x1s = np.linspace(3,12,2)
x0, x1 = np.meshgrid(x0s, x1s)
x0s ,x1s ,x0, x1

(array([ 2., 15.]),
 array([ 3., 12.]),
 array([[ 2., 15.],
        [ 2., 15.]]),
 array([[ 3.,  3.],
        [12., 12.]]))

x1.ravel()

array([ 3.,  3., 12., 12.])

x0.ravel()

array([ 2., 15.,  2., 15.])

X = np.c_[x0.ravel(), x1.ravel()]
X.shape,X

((4, 2),
 array([[ 2.,  3.],
        [15.,  3.],
        [ 2., 12.],
        [15., 12.]]))

y_pred=np.array([[1,0],[0,1]])

 np.meshgrid(x0s, x1s)

[array([[ 2., 15.],
        [ 2., 15.]]),
 array([[ 3.,  3.],
        [12., 12.]])]

X = np.c_[x0.ravel(), x1.ravel()]
X.shape,x0.shape

((4, 2), (2, 2))

x0

array([[ 2., 15.],
       [ 2., 15.]])

7.2 绘制高高线表示预测结果

def plot_predictions(clf, axes):
    x0s = np.linspace(axes[0], axes[1], 100)
    x1s = np.linspace(axes[2], axes[3], 100)
    x0, x1 = np.meshgrid(x0s, x1s)
    X = np.c_[x0.ravel(), x1.ravel()]
    y_pred = clf.predict(X).reshape(x0.shape)
    y_decision = clf.decision_function(X).reshape(x0.shape)

    plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
    plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)

7.3 绘制原始数据

def plot_dataset(X, y, axes):
    plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
    plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
    plt.axis(axes)
    plt.grid(True, which='both')
    plt.xlabel(r"$x_1$", fontsize=20)
    plt.ylabel(r"$x_2$", fontsize=20, rotation=0)

7.4 绘制不同gamma和C对应的

from sklearn.svm import SVC

X, y = make_moons(n_samples=100, noise=0.15, random_state=42)
gamma1, gamma2 = 0.1, 5
C1, C2 = 0.001, 1000
hyperparams = (gamma1, C1), (gamma1, C2), (gamma2, C1), (gamma2, C2)

svm_clfs = []
for gamma, C in hyperparams:
    rbf_kernel_svm_clf = Pipeline([("scaler", StandardScaler()),
                                   ("svm_clf",SVC(kernel="rbf", gamma=gamma, C=C))])
    rbf_kernel_svm_clf.fit(X, y)
    svm_clfs.append(rbf_kernel_svm_clf)

plt.figure(figsize=(6,4))

for i, svm_clf in enumerate(svm_clfs):
    plt.subplot(221 + i)
    plot_predictions(svm_clf, [-1.5, 2.5, -1, 1.5])
    plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])

    gamma, C = hyperparams[i]
    plt.title(r"$\gamma = {}, C = {}$".format(gamma, C), fontsize=12)

plt.show()

实例8* 手写SVM

8.1 创建数据

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import  train_test_split
import matplotlib.pyplot as plt
%matplotlib inline

# data
def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, [0, 1, -1]])
    for i in range(len(data)):
        if data[i,-1] == 0:
            data[i,-1] = -1
    return data[:,:2], data[:,-1]

X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)

plt.scatter(X[:50,0],X[:50,1], label='0')
plt.scatter(X[50:,0],X[50:,1], label='1')
plt.legend()

8.2 定义支持向量机

class SVM:
    def __init__(self, max_iter=100, kernel='linear'):
        self.max_iter = max_iter
        self._kernel = kernel

    def init_args(self, features, labels):
        self.m, self.n = features.shape
        self.X = features
        self.Y = labels
        self.b = 0.0

        # 将Ei保存在一个列表里
        self.alpha = np.ones(self.m)
        self.E = [self._E(i) for i in range(self.m)]
        # 松弛变量
        self.C = 1.0

    def _KKT(self, i):
        y_g = self._g(i) * self.Y[i]
        if self.alpha[i] == 0:
            return y_g >= 1
        elif 0 < self.alpha[i] < self.C:
            return y_g == 1
        else:
            return y_g <= 1

    # g(x)预测值，输入xi（X[i]）
    def _g(self, i):
        r = self.b
        for j in range(self.m):
            r += self.alpha[j] * self.Y[j] * self.kernel(self.X[i], self.X[j])
        return r

    # 核函数
    def kernel(self, x1, x2):
        if self._kernel == 'linear':
            return sum([x1[k] * x2[k] for k in range(self.n)])
        elif self._kernel == 'poly':
            return (sum([x1[k] * x2[k] for k in range(self.n)]) + 1)**2

        return 0

    # E（x）为g(x)对输入x的预测值和y的差
    def _E(self, i):
        return self._g(i) - self.Y[i]

    def _init_alpha(self):
        # 外层循环首先遍历所有满足0
        index_list = [i for i in range(self.m) if 0 < self.alpha[i] < self.C]
        # 否则遍历整个训练集
        non_satisfy_list = [i for i in range(self.m) if i not in index_list]
        index_list.extend(non_satisfy_list)

        for i in index_list:
            if self._KKT(i):
                continue

            E1 = self.E[i]
            # 如果E2是+，选择最小的；如果E2是负的，选择最大的
            if E1 >= 0:
                j = min(range(self.m), key=lambda x: self.E[x])
            else:
                j = max(range(self.m), key=lambda x: self.E[x])
            return i, j

    def _compare(self, _alpha, L, H):
        if _alpha > H:
            return H
        elif _alpha < L:
            return L
        else:
            return _alpha

    def fit(self, features, labels):
        self.init_args(features, labels)

        for t in range(self.max_iter):
            # train
            i1, i2 = self._init_alpha()

            # 边界
            if self.Y[i1] == self.Y[i2]:
                L = max(0, self.alpha[i1] + self.alpha[i2] - self.C)
                H = min(self.C, self.alpha[i1] + self.alpha[i2])
            else:
                L = max(0, self.alpha[i2] - self.alpha[i1])
                H = min(self.C, self.C + self.alpha[i2] - self.alpha[i1])

            E1 = self.E[i1]
            E2 = self.E[i2]
            # eta=K11+K22-2K12
            eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(
                self.X[i2],
                self.X[i2]) - 2 * self.kernel(self.X[i1], self.X[i2])
            if eta <= 0:
                # print('eta <= 0')
                continue

            alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (
                E1 - E2) / eta  #此处有修改，根据书上应该是E1 - E2，书上130-131页
            alpha2_new = self._compare(alpha2_new_unc, L, H)

            alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (
                self.alpha[i2] - alpha2_new)

            b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (
                alpha1_new - self.alpha[i1]) - self.Y[i2] * self.kernel(
                    self.X[i2],
                    self.X[i1]) * (alpha2_new - self.alpha[i2]) + self.b
            b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (
                alpha1_new - self.alpha[i1]) - self.Y[i2] * self.kernel(
                    self.X[i2],
                    self.X[i2]) * (alpha2_new - self.alpha[i2]) + self.b

            if 0 < alpha1_new < self.C:
                b_new = b1_new
            elif 0 < alpha2_new < self.C:
                b_new = b2_new
            else:
                # 选择中点
                b_new = (b1_new + b2_new) / 2

            # 更新参数
            self.alpha[i1] = alpha1_new
            self.alpha[i2] = alpha2_new
            self.b = b_new

            self.E[i1] = self._E(i1)
            self.E[i2] = self._E(i2)
        return 'train done!'

    def predict(self, data):
        r = self.b
        for i in range(self.m):
            r += self.alpha[i] * self.Y[i] * self.kernel(data, self.X[i])

        return 1 if r > 0 else -1

    def score(self, X_test, y_test):
        right_count = 0
        for i in range(len(X_test)):
            result = self.predict(X_test[i])
            if result == y_test[i]:
                right_count += 1
        return right_count / len(X_test)

    def _weight(self):
        # linear model
        yx = self.Y.reshape(-1, 1) * self.X
        self.w = np.dot(yx.T, self.alpha)
        return self.w

8.3 初始化支持向量机并拟合

svm = SVM(max_iter=100)
svm.fit(X_train, y_train)

'train done!'

8.4 支持向量机得到分数

svm.score(X_test, y_test)

0.72

实验1 采用以下数据作为数据集，分别基于线性和核支持向量机进行分类，对于线性核绘制决策边界

1 获取数据

from sklearn.svm import SVC
from sklearn import datasets
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]  # petal length, petal width
y = iris["target"]
X,y

(array([[1.4, 0.2],
        [1.4, 0.2],
        [1.3, 0.2],
        [1.5, 0.2],
        [1.4, 0.2],
        [1.7, 0.4],
        [1.4, 0.3],
        [1.5, 0.2],
        [1.4, 0.2],
        [1.5, 0.1],
        [1.5, 0.2],
        [1.6, 0.2],
        [1.4, 0.1],
        [1.1, 0.1],
        [1.2, 0.2],
        [1.5, 0.4],
        [1.3, 0.4],
        [1.4, 0.3],
        [1.7, 0.3],
        [1.5, 0.3],
        [1.7, 0.2],
        [1.5, 0.4],
        [1. , 0.2],
        [1.7, 0.5],
        [1.9, 0.2],
        [1.6, 0.2],
        [1.6, 0.4],
        [1.5, 0.2],
        [1.4, 0.2],
        [1.6, 0.2],
        [1.6, 0.2],
        [1.5, 0.4],
        [1.5, 0.1],
        [1.4, 0.2],
        [1.5, 0.2],
        [1.2, 0.2],
        [1.3, 0.2],
        [1.4, 0.1],
        [1.3, 0.2],
        [1.5, 0.2],
        [1.3, 0.3],
        [1.3, 0.3],
        [1.3, 0.2],
        [1.6, 0.6],
        [1.9, 0.4],
        [1.4, 0.3],
        [1.6, 0.2],
        [1.4, 0.2],
        [1.5, 0.2],
        [1.4, 0.2],
        [4.7, 1.4],
        [4.5, 1.5],
        [4.9, 1.5],
        [4. , 1.3],
        [4.6, 1.5],
        [4.5, 1.3],
        [4.7, 1.6],
        [3.3, 1. ],
        [4.6, 1.3],
        [3.9, 1.4],
        [3.5, 1. ],
        [4.2, 1.5],
        [4. , 1. ],
        [4.7, 1.4],
        [3.6, 1.3],
        [4.4, 1.4],
        [4.5, 1.5],
        [4.1, 1. ],
        [4.5, 1.5],
        [3.9, 1.1],
        [4.8, 1.8],
        [4. , 1.3],
        [4.9, 1.5],
        [4.7, 1.2],
        [4.3, 1.3],
        [4.4, 1.4],
        [4.8, 1.4],
        [5. , 1.7],
        [4.5, 1.5],
        [3.5, 1. ],
        [3.8, 1.1],
        [3.7, 1. ],
        [3.9, 1.2],
        [5.1, 1.6],
        [4.5, 1.5],
        [4.5, 1.6],
        [4.7, 1.5],
        [4.4, 1.3],
        [4.1, 1.3],
        [4. , 1.3],
        [4.4, 1.2],
        [4.6, 1.4],
        [4. , 1.2],
        [3.3, 1. ],
        [4.2, 1.3],
        [4.2, 1.2],
        [4.2, 1.3],
        [4.3, 1.3],
        [3. , 1.1],
        [4.1, 1.3],
        [6. , 2.5],
        [5.1, 1.9],
        [5.9, 2.1],
        [5.6, 1.8],
        [5.8, 2.2],
        [6.6, 2.1],
        [4.5, 1.7],
        [6.3, 1.8],
        [5.8, 1.8],
        [6.1, 2.5],
        [5.1, 2. ],
        [5.3, 1.9],
        [5.5, 2.1],
        [5. , 2. ],
        [5.1, 2.4],
        [5.3, 2.3],
        [5.5, 1.8],
        [6.7, 2.2],
        [6.9, 2.3],
        [5. , 1.5],
        [5.7, 2.3],
        [4.9, 2. ],
        [6.7, 2. ],
        [4.9, 1.8],
        [5.7, 2.1],
        [6. , 1.8],
        [4.8, 1.8],
        [4.9, 1.8],
        [5.6, 2.1],
        [5.8, 1.6],
        [6.1, 1.9],
        [6.4, 2. ],
        [5.6, 2.2],
        [5.1, 1.5],
        [5.6, 1.4],
        [6.1, 2.3],
        [5.6, 2.4],
        [5.5, 1.8],
        [4.8, 1.8],
        [5.4, 2.1],
        [5.6, 2.4],
        [5.1, 2.3],
        [5.1, 1.9],
        [5.9, 2.3],
        [5.7, 2.5],
        [5.2, 2.3],
        [5. , 1.9],
        [5.2, 2. ],
        [5.4, 2.3],
        [5.1, 1.8]]),
 array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
        0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
        2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
        2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]))

X_train=X[(y==1) | (y==2)]
y_train=y[(y==1) | (y==2)]

y_train

array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

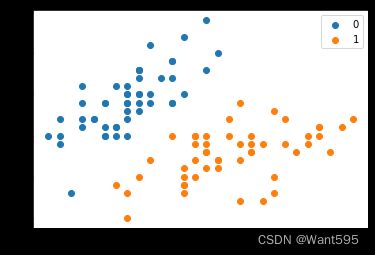
2 可视化数据

plt.scatter(X_train[:50,0],X_train[:50,1],marker='x',label='Positive')
plt.scatter(X_train[50:,0],X_train[50:,1],marker='o',label='Negative')
plt.legend()

3 试试采用线性支持向量机来拟合

from sklearn.svm import SVC
svm_clf = SVC(kernel="linear", C=10,max_iter=1000)
svm_clf.fit(X_train,y_train)

SVC(C=10, kernel='linear', max_iter=1000)

svm_clf.score(X_train,y_train)

0.95

4 试试采用核支持向量机

import sklearn.svm as svm
nl_svc=svm.SVC(C=1,gamma=1,probability=True)
nl_svc.fit(X_train,y_train)
nl_svc.score(X_train,y_train)

0.95

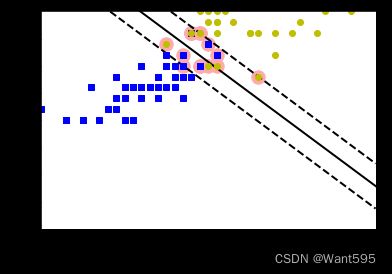
5 绘制线性支持向量机的决策边界

def plot_svc_decision_boundary(svm_clf, xmin, xmax):
    
    w = svm_clf.coef_[0]
    b = svm_clf.intercept_[0]

    # At the decision boundary, w0*x0 + w1*x1 + b = 0
    # => x1 = -w0/w1 * x0 - b/w1
    x0 = np.linspace(xmin, xmax, 200)
    decision_boundary = -w[0]/w[1] * x0 - b/w[1]

    # margin = 1/np.sqrt(w[1]**2+w[0]**2)
    margin = 1/0.9
    
    margin = 1/w[1]
    
    gutter_up = decision_boundary + margin
    gutter_down = decision_boundary - margin

    svs = svm_clf.support_vectors_
    plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#FFAAAA')
    plt.plot(x0, decision_boundary, "k-", linewidth=2)
    plt.plot(x0, gutter_up, "k--", linewidth=2)
    plt.plot(x0, gutter_down, "k--", linewidth=2)

np.min(X_train[:,0]),np.max(X_train[:,0])

(3.0, 6.9)

plt.figure(figsize=(6,4))
plot_svc_decision_boundary(svm_clf,3,7)
plt.plot(X[:, 0][y == 1], X[:, 1][y == 1], "bs")
plt.plot(X[:, 0][y == 2], X[:, 1][y == 2], "yo")
plt.xlabel("Petal length", fontsize=14)
plt.axis([3,7,0,2])
plt.show()

6 绘制非线性决策边界

def plot_predictions(clf, axes):
    x0s = np.linspace(axes[0], axes[1], 100)
    x1s = np.linspace(axes[2], axes[3], 100)
    x0, x1 = np.meshgrid(x0s, x1s)
    X = np.c_[x0.ravel(), x1.ravel()]
    y_pred = clf.predict(X).reshape(x0.shape)
    y_decision = clf.decision_function(X).reshape(x0.shape)

    plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
    plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)

def plot_dataset(X, y, axes):
    plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs")
    plt.plot(X[:, 0][y==2], X[:, 1][y==2], "g^")
    plt.axis(axes)
    plt.grid(True, which='both')
    plt.xlabel(r"$x_1$", fontsize=20)
    plt.ylabel(r"$x_2$", fontsize=20, rotation=0)

np.min(X_train[:,0]),np.max(X_train[:,0]),

(3.0, 6.9)

np.min(X_train[:,1]),np.max(X_train[:,1])

(1.0, 2.5)

plot_predictions(nl_svc, [2.5,7,1,3])
plot_dataset(X, y, [2.5,7,1,3])

你可能感兴趣的:(《,Python机器学习入门实验,》,机器学习,python,支持向量机)

【Python】一文详细介绍 py格式文件高斯小哥 Python基础【高质量合集】python 新手入门学习
【Python】一文详细介绍py格式文件个人主页：高斯小哥高质量专栏：Matplotlib之旅：零基础精通数据可视化、Python基础【高质量合集】、PyTorch零基础入门教程希望得到您的订阅和支持~创作高质量博文(平均质量分92+)，分享更多关于深度学习、PyTorch、Python领域的优质内容！（希望得到您的关注~）文章目录一、py格式文件简介二、如何创建和编辑py格式文件三、如何运行py
python抓包与解包_Python—网络抓包与解包（pcap、dpkt） weixin_39691055 python抓包与解包
pcap安装[root@localhost~]#pipinstallpypcap抓包与解包#-*-coding:utf-8-*-importpcap,dpktimportre,threading,requests__black_ip=['103.224.249.123','203.66.1.212']#抓包：param1eth_name网卡名，如：eth0,eth3。param2p_type日志捕
华为OD机试 - 单向链表中间节点（Java & JS & Python & C & C++）华为OD题库华为od 链表 java
须知哈喽，本题库完全免费，收费是为了防止被爬，大家订阅专栏后可以私信联系退款。感谢支持文章目录须知题目描述输出描述解析代码题目描述给定一个单链表L，请编写程序输出L中间结点保存的数据。如果有两个中间结点，则输出第二个中间结点保存的数据。例如：给定L为1→7→5，则输出应该为7；给定L为1→2→3→4，则输出应该为3；输入描述每个输入包含1个测试用例。每个测试用例：第一行给出链表首结点的地址、结点总
python 推导式(派生、衍生) sanduo112 人工智能 python windows 开发语言
python推导式一、推导式(派生、衍生)1.Python推导式是一种独特的数据处理方式，可以从一个数据序列构建另一个新的数据序列的结构体。2.列表(list)推导式3.字典(dict)推导式4.集合(set)推导式5.元组(tuple)推导式二、代码概述一、推导式(派生、衍生)1.Python推导式是一种独特的数据处理方式，可以从一个数据序列构建另一个新的数据序列的结构体。Python支持各种数
数据挖掘|数据预处理|基于Python的数据标准化方法皖山文武数据挖掘数据建模与分析 python 数据挖掘开发语言
基于Python的数据标准化方法1.z-score方法2.极差标准化方法3.最大绝对值标准化方法在数据分析之前，通常需要先将数据标准化（Standardization），利用标准化后的数据进行数据分析，以避免属性之间不同度量和取值范围差异造成数据对分析结果的影响。1.z-score方法Z-score方法是基于原始数据的均值和标准差来进行数据标准化的，处理后的数据均值为0，方差为1，符合标准正态分布
CSV指南：Python程序获取大型CSV文件行数孤独打铁匠Julian 笔记经验分享 python
本指南提供了几种使用Python来获取大型CSV文件行数的方法，并解释了每种方法的适用场景。方法1:使用csv.reader处理复杂CSV文件当你的CSV文件中包含多行字段（即某些字段的值中包含换行符）时，使用csv.reader是一个可靠的选择，因为它能够正确处理这些复杂情况。这个方法适用于大多数大小的CSV文件，但是对于非常大的文件，读取整个文件可能会占用较多的时间和内存。对于极大的文件，考虑
谷歌浏览器驱动Chromedriver（114-120版本）文件以及驱动下载教程 pigerr杨 Python python chrome drivers
ChromeDriver官方网站GitHub||GoogleChromeLabs/chrome-for-testingChromeDriver113-125_JSONChromeforTestingavailability123-125zip白月黑羽Python基础|进阶|Qt图形界面|Django|自动化测试|性能测试|JS语言|JS前端|原理与安装
大创项目推荐深度学习 opencv python 公式识别(图像识别机器视觉) laafeer python
文章目录0前言1课题说明2效果展示3具体实现4关键代码实现5算法综合效果6最后0前言优质竞赛项目系列，今天要分享的是基于深度学习的数学公式识别算法实现该项目较为新颖，适合作为竞赛课题方向，学长非常推荐！学长这里给一个题目综合评分(每项满分5分)难度系数：3分工作量：4分创新点：4分更多资料,项目分享：https://gitee.com/dancheng-senior/postgraduate1课题
不了解孩子，哪来的尊重孩子敏贰好学
著名的棉花糖实验创始人、美国心理学家沃尔特·米歇尔发现，如果父母支持孩子的选择和决定，鼓励孩子的自主性，孩子后期会展现更强的认知和控制注意力的能力。也就是说，父母越让孩子自由，孩子反而越能自控。这是为什么呢？道理很简
ES-LTR粗排模块 poins jenkins 运维
ES-LTR粗排模块官方资源：https://github.com/HeiBoWang/elasticsearch-learning-to-rankElasticsearch学习排名插件使用机器学习提高搜索相关性排名。它为维基媒体基金会和Snagajob等地方的搜索提供了动力！这个插件有什么功能此插件：允许您在Elasticsearch中存储特征（Elasticsearch查询模板）记录特征得分（
RabbitMQ 实验消费原始队列消息，拒绝（reject）投递死信交换机过程熊明才 rabbitmq 分布式
如果你想通过RabbitMQ的死信队列功能实现消费者拒绝消息投递到死信交换机的行为，你可以按照以下步骤操作：创建原始队列，并将其绑定到一个交换机上：exportRABBITMQ_SERVER=127.0.0.1exportRABBITMQ_PORT=5672exportRABBITMQ_USER=mingcaiexportRABBITMQ_PASSWORD=passwordrabbitmqadmi
python转码 Desamond python 开发语言
转码在许多场景中都有应用，以下是一些常见的场景：网页开发：当用户在网页上输入文本时，可能需要将特殊字符（如空格、引号、特殊符号等）进行转码，以防止这些字符对URL或HTML代码产生干扰。文件名处理：在处理文件名时，可能需要将特殊字符进行转码，以避免文件名被错误地解析或显示。数据传输：在数据传输过程中，为了确保数据的完整性和正确性，可能需要将数据中的特殊字符进行转码。数据存储：在数据库或数据存储中，
排序算法太多？常用排序都在这了，一篇文章总结和实现所有面试会考的排序算法（基于Python实现）宇宙之一粟不归路之Python #IT面试题收集与总结数据结构与算法算法数据结构排序算法 python java
文章目录排序算法1.常见的排序算法1.1选择排序1.1.1思想1.1.2实现**1.1.3选择排序分析**1.2冒泡排序**1.2.1思想****1.2.2实现****1.2.3冒泡排序分析**1.3插入排序**1.3.1思想****1.3.2实现****1.3.3插入排序分析**1.4归并排序☆☆★**1.4.1思想****1.4.2实现****1.4.3归并排序分析**1.5快速排序☆★★**
【数据结构】实验一实现顺序表各种基本运算的算法张鱼·小丸子数据结构实验 c++数据结构
题目：实现顺序表各种基本运算的算法要求：1、建立一个顺序表，输入n个元素并输出；2、查找线性表中的最大元素并输出；3、在线性表的第i个元素前插入一个正整数x；4、删除线性表中的第j个元素；5、将线性表中的元素按升序排列；6、将线性表中的元素就地逆序（只允许用一个暂存单元）；#include#defineSIZE1000usingnamespacestd;typedefstruct{int*a;//
27.Python从入门到精通—Python异常处理抛出异常用户自定义异常定义清理行为预定义的清理行为以山河作礼。 #Python基础入门—详解版 python java 服务器
27.从入门到精通：Python异常处理抛出异常用户自定义异常定义清理行为预定义的清理行为异常处理抛出异常用户自定义异常定义清理行为预定义的清理行为异常处理在Python中，异常处理是一种处理程序在执行期间可能遇到的错误的方法。当Python解释器遇到错误时，它会引发异常。异常是一种Python对象，它包含有关错误的信息，例如错误类型和错误位置。为了处理异常，您可以使用try-except语句。在
python清华大学出版社答案_Python机器学习及实践 weixin_39805119 python清华大学出版社答案
第1章机器学习的基础知识1.1何谓机器学习1.1.1传感器和海量数据1.1.2机器学习的重要性1.1.3机器学习的表现1.1.4机器学习的主要任务1.1.5选择合适的算法1.1.6机器学习程序的步骤1.2综合分类1.3推荐系统和深度学习1.3.1推荐系统1.3.2深度学习1.4何为Python1.4.1使用Python软件的由来1.4.2为什么使用Python1.4.3Python设计定位1.4.
Python | Redis工具类 -拟墨画扇- Python redis 数据库缓存 python
一、需求自动连接Redis数据库，通过连接池处理数据对输出结果进行Log打印并保存到文件二、代码Utils.redisUtils.py#!/usr/bin/envpython#-*-coding:utf-8-*-importredisfromUtils.loggerimportlog"""Redis数据格式(1)字符串|存储形式:key-value:str-存储二进制数据:可以存储任意类型的数据，
Python dict字符串转json对象，小数精度丢失问题朝如青丝暮成雪 json python
一前言JSON(JavaScriptObjectNotation)是一种轻量级的数据交换格式，dict是Python的一种数据格式。本篇介绍一个float数据转换时精度丢失的案例。二问题描述importjsontest_str1='{"π":3.1415926535897932384626433832795028841971}'test_str2='{"value":10.00000}'print
C语言pthread互斥锁(mutex)和可重入锁(递归锁recursive)的演示嫦娥妹妹等等我开发语言 c语言
实验理论参考:1一旦共享资源被互斥锁锁定,则其余线程想访问共享资源必须等待，直到锁被释放2使用normal属性的互斥锁,一旦发生重入逻辑,则阻塞,成为死锁需要将属性改为recursive成为可重入的,递归的代码功能:1命令行传参1model=1演示异步未上锁之乱序演示count在数据竞态（RaceCondition）下的错误值2命令行传参2model=2演示使用互斥锁后线程的执行顺序演示count
UNDERSTANDING HTML WITH LARGE LANGUAGE MODELS liferecords LLM 语言模型人工智能自然语言处理
UNDERSTANDINGHTMLWITHLARGELANGUAGEMODELS相关链接：arXiv关键字：大型语言模型、HTML理解、Web自动化、自然语言处理、机器学习摘要大型语言模型（LLMs）在各种自然语言任务上表现出色。然而，它们在HTML理解方面的能力——即解析网页的原始HTML，对于自动化基于Web的任务、爬取和浏览器辅助检索等应用——尚未被充分探索。我们为HTML理解模型（经过微调
Python+Requests模拟发送GET请求爱学习的执念自动化测试软件测试技术分享 python 开发语言
模拟发送GET请求前置条件：导入requests库一、发送不带参数的get请求代码如下：以百度首页为例importrequests#发送get请求response=requests.get(url="http://www.baidu.com")print(response.content.decode("utf-8"))#以utf-8的编码输出内容二、发送带参数的get请求发送带参数的get请求有
Python极速入门：五分钟开启实战之旅！知白守黑V Python 编程语言系统运维 python 编程语言 python开发 python学习 python入门 python数据分析
1.Python基础语法和结构：了解Python的基本语法，包括变量、数据类型、运算符、注释等。控制流：掌握条件语句（if-elif-else）、循环（for和while）及其控制（break和continue）。函数：学习如何定义和使用函数，包括参数传递、返回值、作用域和闭包。模块和包：理解如何导入和使用模块，以及如何创建和使用自己的包。2.数据处理列表、元组和集合：学习这些序列类型的操作和方法
Python Flask 使用数据库安果移不动 python flask 开发语言
pipinstallflask_sqlalchemy官方文档：Flask-SQLAlchemy—Flask-SQLAlchemyDocumentation(3.1.x)为了不报错也需要导入另外两个库#pipinstallflask_sqlalchemy#pipinstallmysqlclient完整代码importosfromflaskimportFlaskfromflask_sqlalchemy
PaperWeekly sapienst Papers PaperwithCode General ML
1.Python软件包解决DL在未见过的数据分布下性能差的问题：（1）神经网络和损失分离的模块化设计（2）强大便捷的基准测试能力（3）易于使用但难以修改（4）github:https://github.com/marrlab/domainlabTrainer和Models之间是什么关系Trainer和Models是DomainLab中的两个核心概念。Trainer是一个用于指导数据流向模型并计算S
使用Python读取Excel文件并计算平均分嘻嘻爱编码 Python从入门到放弃 python excel 开发语言
在这篇博客中，我们将探讨如何使用Python的pandas库来读取Excel文件，并计算其中数据的平均分。pandas是一个强大的数据分析工具，它允许我们以简单直观的方式处理表格数据。安装必要的库在开始之前，确保你的环境中安装了pandas和openpyxl库。可以使用以下命令进行安装：pipinstallpandasopenpyxl读取Excel文件首先，我们需要读取Excel文件。假设我们有一
python项目练习——7.网站访问日志分析器 F—— python项目练习 python 信息可视化数据分析数据挖掘开发语言学习
项目功能分析：这个项目可以读取网站的访问日志文件，统计访问量、独立访客数、访问来源等信息，并以图表或表格的形式展示出来。这个项目涉及到文件操作、数据处理、数据可视化等方面的技术。示例代码：importrefromcollectionsimportCounterimportmatplotlib.pyplotaspltdefparse_log_file(log_file):#读取日志文件内容witho
python的while双重循环九九乘法表 Jinm_R python 开发语言
a=1whilea<=9:b=1#乘数每次需要从1开始whileb<=a:print(f"{a}*{b}={a*b}\t",end='')#\t为制表符使乘法表整齐end=''代表用空格代替换行b+=1a+=1print()#乘数每加一换行
【Python】成功解决ModuleNotFoundError: No module named ‘torchinfo‘ 高斯小哥 BUG解决方案合集 python pytorch 新手入门学习 debug
【Python】成功解决ModuleNotFoundError:Nomodulenamed‘torchinfo’个人主页：高斯小哥高质量专栏：Matplotlib之旅：零基础精通数据可视化、Python基础【高质量合集】、PyTorch零基础入门教程希望得到您的订阅和支持~创作高质量博文(平均质量分92+)，分享更多关于深度学习、PyTorch、Python领域的优质内容！（希望得到您的关注~）文
OpenCV（一个C++人工智能领域重要开源基础库）简介愚梦者 OpenCV 人工智能人工智能 opencv c++图像处理计算机视觉开源
返回：OpenCV系列文章目录（持续更新中......）上一篇：OpenCV4.9.0配置选项参考下一篇：OpenCV4.9.0开源计算机视觉库安装概述引言：OpenCV（全称OpenSourceComputerVisionLibrary）是一个基于开放源代码发行的跨平台计算机视觉库，可以用来进行图像处理、计算机视觉和机器学习等领域的开发。该库由英特尔公司于1999年开始开发，最初是为了加速处理器
Python自动化测试web常见框架汇总自动化测试薰儿软件测试技术分享 python 前端开发语言
1、前言目前，有非常多的Python框架，用来帮助你更轻松的创建web应用。这些框架把相应的模块组织起来，使得构建应用的时候可以更快捷，也不用去关注一些细节（例如socket和协议），所以需要的都在框架里了。接下来我们会介绍不同的选项。经过初期的不起眼，Python已经成为互联网最流行的服务端编程语言之一。根据W3Techs的统计，它被用于很多的大流量的站点很多的大流量的站点很多的大流量的站点，超
jdk tomcat 环境变量配置 Array_06 java jdk tomcat
Win7 下如何配置java环境变量 1。准备jdk包，win7系统，tomcat安装包（均上网下载即可） 2。进行对jdk的安装，尽量为默认路径（但要记住啊！！以防以后配置用。。。） 3。分别配置高级环境变量。电脑-->右击属性-->高级环境变量-->环境变量。分别配置 : path &nbs
Spring调SDK包报java.lang.NoSuchFieldError错误 bijian1013 java spring
在工作中调另一个系统的SDK包，出现如下java.lang.NoSuchFieldError错误。 org.springframework.web.util.NestedServletException: Handler processing failed; nested exception is java.l
LeetCode[位运算] - #136 数组中的单一数 Cwind java 题解位运算 LeetCode Algorithm
原题链接：#136 Single Number 要求：给定一个整型数组，其中除了一个元素之外，每个元素都出现两次。找出这个元素注意：算法的时间复杂度应为O(n)，最好不使用额外的内存空间难度：中等分析：题目限定了线性的时间复杂度，同时不使用额外的空间，即要求只遍历数组一遍得出结果。由于异或运算 n XOR n = 0, n XOR 0 = n，故将数组中的每个元素进
qq登陆界面开发 15700786134 qq
今天我们来开发一个qq登陆界面，首先写一个界面程序，一个界面首先是一个Frame对象，即是一个窗体。然后在这个窗体上放置其他组件。代码如下： public class First { public void initul(){ jf=ne
Linux的程序包管理器RPM 被触发 linux
在早期我们使用源代码的方式来安装软件时，都需要先把源程序代码编译成可执行的二进制安装程序，然后进行安装。这就意味着每次安装软件都需要经过预处理-->编译-->汇编-->链接-->生成安装文件--> 安装，这个复杂而艰辛的过程。为简化安装步骤，便于广大用户的安装部署程序，程序提供商就在特定的系统上面编译好相关程序的安装文件并进行打包，提供给大家下载，我们只需要根据自己的
socket通信遇到EOFException 肆无忌惮_ EOFException
java.io.EOFException at java.io.ObjectInputStream$PeekInputStream.readFully(ObjectInputStream.java:2281) at java.io.ObjectInputStream$BlockDataInputStream.readShort(ObjectInputStream.java:
基于spring的web项目定时操作知了ing java Web
废话不多说，直接上代码，很简单配置一下项目启动就行 1，web.xml <?xml version="1.0" encoding="UTF-8"?> <web-app xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance" xmlns="h
树形结构的数据库表Schema设计矮蛋蛋 schema
原文地址： http://blog.csdn.net/MONKEY_D_MENG/article/details/6647488 程序设计过程中，我们常常用树形结构来表征某些数据的关联关系，如企业上下级部门、栏目结构、商品分类等等，通常而言，这些树状结构需要借助于数据库完成持久化。然而目前的各种基于关系的数据库，都是以二维表的形式记录存储数据信息，
maven将jar包和源码一起打包到本地仓库 alleni123 maven
http://stackoverflow.com/questions/4031987/how-to-upload-sources-to-local-maven-repository <project> ... <build> <plugins> <plugin> <groupI
java IO操作与 File 获取文件或文件夹的大小，可读，等属性！！！百合不是茶
类 File File是指文件和目录路径名的抽象表示形式。 1，何为文件：标准文件（txt doc mp3...）目录文件（文件夹）虚拟内存文件 2，File类中有可以创建文件的 createNewFile（）方法,在创建新文件的时候需要try{} catch(）{}因为可能会抛出异常；也有可以判断文件是否是一个标准文件的方法isFile();这些防抖都
Spring注入有继承关系的类（2） bijian1013 java spring
被注入类的父类有相应的属性，Spring可以直接注入相应的属性，如下所例：1.AClass类 package com.bijian.spring.test4; public class AClass { private String a; private String b; public String getA() { retu
30岁转型期你能否成为成功人士 bijian1013 成长励志
很多人由于年轻时走了弯路，到了30岁一事无成，这样的例子大有人在。但同样也有一些人，整个职业生涯都发展得很优秀，到了30岁已经成为职场的精英阶层。由于做猎头的原因，我们接触很多30岁左右的经理人，发现他们在职业发展道路上往往有很多致命的问题。在30岁之前，他们的职业生涯表现很优秀，但从30岁到40岁这一段，很多人
【Velocity四】Velocity与Java互操作 bit1129 velocity
Velocity出现的目的用于简化基于MVC的web应用开发，用于替代JSP标签技术，那么Velocity如何访问Java代码.本篇继续以Velocity三http://bit1129.iteye.com/blog/2106142中的例子为基础， POJO package com.tom.servlets; public
【Hive十一】Hive数据倾斜优化 bit1129 hive
什么是Hive数据倾斜问题操作：join,group by,count distinct 现象：任务进度长时间维持在99%（或100%），查看任务监控页面，发现只有少量（1个或几个）reduce子任务未完成；查看未完成的子任务，可以看到本地读写数据量积累非常大，通常超过10GB可以认定为发生数据倾斜。原因：key分布不均匀倾斜度衡量：平均记录数超过50w且
在nginx中集成lua脚本：添加自定义Http头，封IP等 ronin47 nginx lua csrf
Lua是一个可以嵌入到Nginx配置文件中的动态脚本语言，从而可以在Nginx请求处理的任何阶段执行各种Lua代码。刚开始我们只是用Lua 把请求路由到后端服务器，但是它对我们架构的作用超出了我们的预期。下面就讲讲我们所做的工作。强制搜索引擎只索引mixlr.com Google把子域名当作完全独立的网站，我们不希望爬虫抓取子域名的页面，降低我们的Page rank。 location /{
java-3.求子数组的最大和 bylijinnan java
package beautyOfCoding; public class MaxSubArraySum { /** * 3.求子数组的最大和题目描述：输入一个整形数组，数组里有正数也有负数。数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。求所有子数组的和的最大值。要求时间复杂度为O(n)。例如输入的数组为1, -2, 3, 10, -4,
Netty源码学习-FileRegion bylijinnan java netty
今天看org.jboss.netty.example.http.file.HttpStaticFileServerHandler.java 可以直接往channel里面写入一个FileRegion对象，而不需要相应的encoder： //pipeline（没有诸如“FileRegionEncoder”的handler）： public ChannelPipeline ge
使用ZeroClipboard解决跨浏览器复制到剪贴板的问题 cngolon 跨浏览器复制到粘贴板 Zero Clipboard
Zero Clipboard的实现原理 Zero Clipboard 利用透明的Flash让其漂浮在复制按钮之上，这样其实点击的不是按钮而是 Flash ，这样将需要的内容传入Flash，再通过Flash的复制功能把传入的内容复制到剪贴板。 Zero Clipboard的安装方法首先需要下载 Zero Clipboard的压缩包，解压后把文件夹中两个文件：ZeroClipboard.js
单例模式 cuishikuan 单例模式
第一种（懒汉，线程不安全）： public class Singleton { 2 private static Singleton instance; 3 pri
spring+websocket的使用 dalan_123
一、spring配置文件 <?xml version="1.0" encoding="UTF-8"?><beans xmlns="http://www.springframework.org/schema/beans" xmlns:xsi="http://www.w3.or
细节问题：ZEROFILL的用法范围。 dcj3sjt126com mysql
1、zerofill把月份中的一位数字比如1，2，3等加前导0 mysql> CREATE TABLE t1 (year YEAR(4), month INT(2) UNSIGNED ZEROFILL, -> day
Android开发10——Activity的跳转与传值 dcj3sjt126com Android开发
Activity跳转与传值，主要是通过Intent类，Intent的作用是激活组件和附带数据。一、Activity跳转方法一Intent intent = new Intent(A.this, B.class); startActivity(intent) 方法二Intent intent = new Intent();intent.setCla
jdbc 得到表结构、主键 eksliang jdbc 得到表结构、主键
转自博客：http://blog.csdn.net/ocean1010/article/details/7266042 假设有个con DatabaseMetaData dbmd = con.getMetaData(); rs = dbmd.getColumns(con.getCatalog(), schema, tableName, null); rs.getSt
Android 应用程序开关GPS gqdy365 android
要在应用程序中操作GPS开关需要权限： <uses-permission android:name="android.permission.WRITE_SECURE_SETTINGS" /> 但在配置文件中添加此权限之后会报错，无法再eclipse里面正常编译，怎么办？ 1、方法一：将项目放到Android源码中编译； 2、方法二：网上有人说cl
Windows上调试MapReduce zhiquanliu mapreduce
1.下载hadoop2x-eclipse-plugin https://github.com/winghc/hadoop2x-eclipse-plugin.git 把 hadoop2.6.0-eclipse-plugin.jar 放到eclipse plugin 目录中。 2.下载 hadoop2.6_x64_.zip http://dl.iteye.com/topics/download/d2b
如何看待一些知名博客推广软文的行为？ justjavac 博客
本文来自我在知乎上的一个回答：http://www.zhihu.com/question/23431810/answer/24588621 互联网上的两种典型心态：当初求种像条狗，如今撸完嫌人丑当初搜贴像条犬，如今读完嫌人软你为啥感觉不舒服呢？难道非得要作者把自己的劳动成果免费给你用，你才舒服？就如同 Google 关闭了 Gooled Reader，那是
sql优化总结 macroli sql
为了是自己对sql优化有更好的原则性，在这里做一下总结，个人原则如有不对请多多指教。谢谢！要知道一个简单的sql语句执行效率，就要有查看方式，一遍更好的进行优化。一、简单的统计语句执行时间 declare @d datetime ---定义一个datetime的变量set @d=getdate() ---获取查询语句开始前的时间select user_id
Linux Oracle中常遇到的一些问题及命令总结超声波 oracle linux
1.linux更改主机名 (1)#hostname oracledb　　　　临时修改主机名 (2) vi /etc/sysconfig/network 　　修改hostname (3) vi /etc/hosts　　　　　　　　修改IP对应的主机名 2.linux重启oracle实例及监听的各种方法（注意操作的顺序应该是先监听，后数据库实例） &nbs
hive函数大全及使用示例 superlxw1234 hadoop hive函数
具体说明及示例参见附件文档。文档目录：目录一、关系运算： 4 1. 等值比较: = 4 2. 不等值比较: <> 4 3. 小于比较: < 4 4. 小于等于比较: <= 4 5. 大于比较: > 5 6. 大于等于比较: >= 5 7. 空值判断: IS NULL 5
Spring 4.2新特性-使用@Order调整配置类加载顺序 wiselyman spring 4
4.1 @Order Spring 4.2 利用@Order控制配置类的加载顺序 4.2 演示两个演示bean package com.wisely.spring4_2.order; public class Demo1Service { } package com.wisely.spring4_2.order; public class