C语言笔试训练【第九天】

1、下列程序的输出是（ ）

#include
int main()
{
	int a[12] = { 1,2,3,4,5,6,7,8,9,10,11,12 }， * p[4], i;
	for (i = 0; i < 4; i++)
		p[i] = &a[i * 3];
	printf("%d\n"，p[3][2]);
	return 0;
}

A: 上述程序有错误 B: 6 C: 8 D: 12

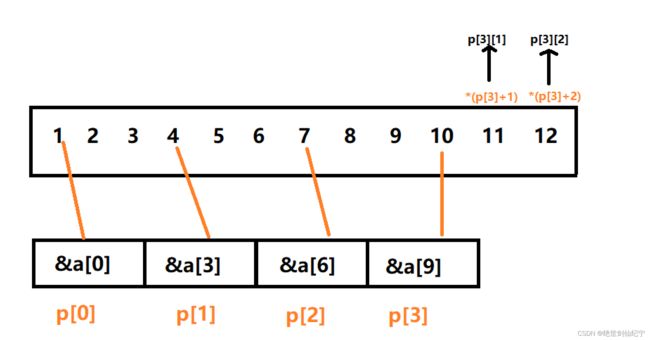
这道题中的数组p里的数据类型为 int* 类型，p是一个指针数组，p[i] = &a[i*3]相当于是把数组a每3个一组分开并把每组的首地址存在p数组，此时p类似一个4行3列的二维数组，p[3][2]就是4行第3个元素12，但二维数组的本质也是一维数组，如图，所以选 D

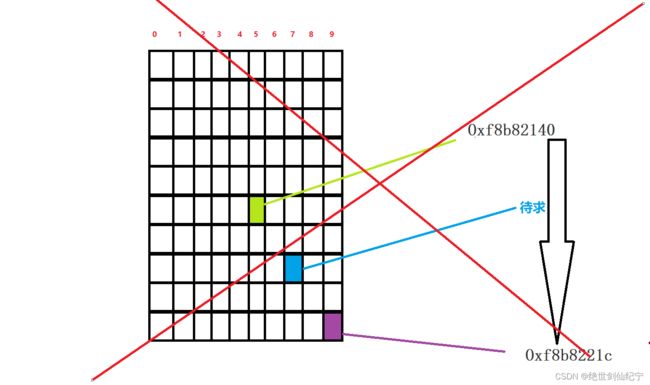
2、二维数组X按行顺序存储，其中每个元素占1个存储单元。若 X[4][4] 的存储地址为 Oxf8b82140 , X[9][9] 的存储地址为 Oxf8b8221c ,则 X[7][7] 的存储地址为（ ）

A: Oxf8b821c4 B: Oxf8b821a6 C: Oxf8b82198 D: Oxf8b821c0**

并不知数组有几行几列，所以不能用普通的数组

假设每行有n个元素：那x[9][9]元素的地址 - x[4][4]元素的地址 = 0x21c-0x140=5n+5(21c和140是地址末三位的十六进制数)，这里n是43，假设x[7][7]的地址是z,x[7][7]元素的地址 - x[4][4]元素的地址 = z-0x140 = 3n+3，z = 3n+3+140 =
3*43+3+0x140 = 0x84+0x140 = 0x1c4，看地址的尾数，选择A

3、以下哪个选项可以正确描述 sizeof(double) （ ）

A: 一个整型表达式 B: 一个双精度型表达式 C: 一个不合法的表达式 D: 一种函数调用

sizeof是C语言中的一个操作符，不是函数调用，简单的说其作用就是返回一个对象或者类型所占的内存字节数，结果是无符
号整数，因此可以把它看作是整型表达式。所以选择 A

4、下列代码运行后的结果是什么（ ）

int main(){
	char a = 'a', b;
	printf("%c,", ++a);
	printf("%c\n", b = a++);
	return 0;
}

A: b,b B: b,c C: a,b D: a,c

变量a里边存的是字符’a’，第一次输出先加加再输出，输出的是’b’;第二次输出的时候，a先赋值再加加，赋值给b的就是a原来
的值，输出b的时候的还是’b’，所以选 A

5、以下逗号表达式的值为（ ）

(x= 4 * 5 , x * 5) , x + 5;

A: 25 B: 20 C: 100 D: 45

逗号表达式是从前到后依次计算子表达式，而其结果是最后一项的值，此题去掉括号后的表达式，和原表达式是等价的，先
计算45并赋值给x，x变为20，中间x5并没有改变x的值，最后一项x+5值是25，也就是整个表达式的值，所以选 A

自除数

自除数
自除数 是指可以被它包含的每一位数整除的数。

例如，128 是一个 自除数 ，因为 128 % 1 = 0，128 % 2 = 0，128 % 8 =0。自除数 不允许包含 0 。

给定两个整数 left 和 right ，返回一个列表，列表的元素是范围 [left, right] 内所有的 自除数 。

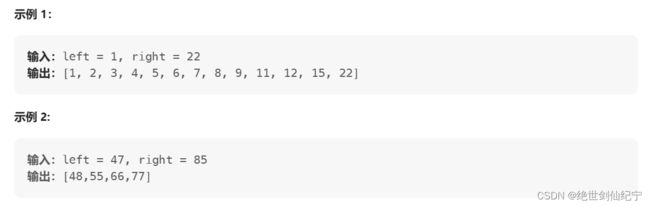
此题只需要将这个数的每一位找出，再用这个数进行取模，看是否等于0即可。但要注意一点，如果这个数中含有0，那他不可能是自除数，因为0不能做除数。

int* selfDividingNumbers(int left, int right, int* returnSize){
    int len=right-left+1;
    int *arr=(int*)malloc(sizeof(int)*len);
    int j=0;
    for(int i=left;i<=right;i++){
        int ret=i;
        while(ret){
            int z=ret%10;
            if(z==0)
                break;
            if(i%z !=0)
                break;
            ret/=10;
        }
        if(ret==0){
            arr[j]=i;
            j++;
        }
    }
    *returnSize=j;
    return arr;
}

除自身以外数组的乘积

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请不要使用除法，且在 O(n) 时间复杂度内完成此题。

题目明确说明不能用除法。当然，使用除法也不一定行的同，因为数组中如果哪个位置为0的话，就不能正常运算，会出错。
这里我看了官方题解的做法，叫左右乘积列表

我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案，而是利用索引左侧所有数字的乘积和右侧所有数字的乘积（即前缀与后缀）相乘得到答案。

对于给定索引 i，我们将使用它左边所有数字的乘积乘以右边所有数字的乘积。下面让我们更加具体的描述这个算法
算法的具体实现步骤（leetcode）

这里就用官方的例子来画图举例

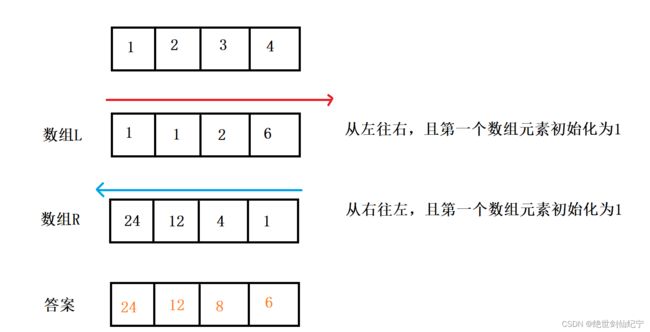
答案对应的位置就是两个数组对应位置的乘积。

int* productExceptSelf(int* nums, int numsSize, int* returnSize){
    int i=0,ret=1;
    int* arr1=(int*)malloc(sizeof(int)*numsSize);
    arr1[0]=1;
    int* arr2=(int*)malloc(sizeof(int)*numsSize);
    arr2[numsSize-1]=1;
    int* arr3=(int*)malloc(sizeof(int)*numsSize);
    for(i=0;i<numsSize-1;i++){
        ret*=nums[i];
        arr1[i+1]=ret;
    }
    ret=1;
    for(i=numsSize-1;i>0;i--){
        ret*=nums[i];
        arr2[i-1]=ret;
    }
    for(i=0;i<numsSize;i++){
        arr3[i]=arr1[i]*arr2[i];
    }
    *returnSize=numsSize;
    return arr3;
}