并查集——你一看就明白就会用

本文分成两个部分，第一部分是基础知识，这一块这篇文章就讲得非常好了，生动有趣又简单易懂，是我见过的最好的算法解说博文。既然它已经做到最好，我就没必要做重复的事情了，就在这里给大家点一个方向。

我要做的是第二部分，就是给出题型模板与刷题。我们不能光会理论，不知道怎么应用。

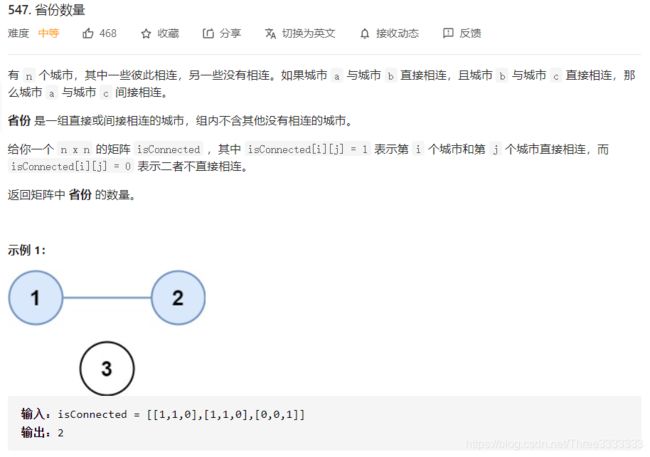
针对于并查集，我选的是力扣547——省份数量。这里先给大家一个截图：

 

针对于这种相连与否的问题，应该想到并查集的方法。

相信这个时候的你已经看完我给你的CSDN博文链接，这样的话，看下面的模板应该会很顺畅：

// 并查集模板
class DisjointSet {
    private:
        int[maxNum] father; // maxNum根据题目要求来设定，比如LC547省份数量，maxNum设置为210即可。
    public:
        void init(int n) { // initialize disjoint set
            for (int i = 0; i < n; i++) {
                father[i] = i;
            }
        }
        // find函数有两种写法
        // 写法一
        int find(int x) {
            int root = x;
            while (root != father[root]) { // 寻根
                root = father[root];
            }
            int originalFather;
            while (x != root) {  // 路径压缩
                originalFather = father[x];
                father[x] = root;
                x = originalFather;
            }
        }
        // 写法二
        int find(int x) {
            return x == father[x] ? x : father[x] = find(father[x]);  // 代码简洁，并且已经有路径压缩包含其中。
        }
        // union的写法
        void union2(int x, int y) { // 这里取名为union2的原因是，union是C++中的一个关键字，以示不同。也可以取名为merge或者join
            int rootX = find(x);
            int rootY = find(y);
            if (rootX != rootY) {
                father[rootX] = rootY; // 合并
            }
        }
        bool same(int x, int y) {
            return find(x) == find(y); // 判断两个元素是不是来自于同一个集合
        }
};
int main() {
    DisjointSet UnionFind;
    int n = ... // 根据题目要求得到
    UnionFind.init(n); // n的来源是题目的内容，对并查集进行初始化
    // 之后根据题目要求进行相应处理即可
}

这里有几点要注意：

1.关于并查集的英文，我在维基百科上面搜到这样的解释：In computer science, a disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that stores a collection of disjoint (non-overlapping) sets. 这就代表并查集的英文也可以叫做disjoint set，虽然大多数人叫union find set。我之所以用disjoint set是因为我第一次接触到的英文是disjoint set，是在Coursera上面的一门课上，我把传送门给大家：巴啦啦能量，传送！（其实不是很推荐这门课，感觉对于新手偏难了。）

2.大家在写并查集的时候，union函数会用别的名称，比如merge或者join，这是因为union是C++中的一个关键字，我们命名的时候要小心，此处我命名为union2，以示区分。

3.在模板中，并查集的初始化是father[x]的每个元素等于其位置，比如father[i] = i。这是一种初始化的方案。可以这么理解：在一开始，大家都没有成立帮派，谁也不服谁，那就都自立门户，自封“太祖”，所以就father[i] = i啦。那么，除了这种初始化还有别的吗？肯定是有的。比如把father定义成一个哈希表，然后用一个特殊的value（比如-1）表明初始化的节点或者新加入的节点。这种做法可以参考力扣中的一个题解。

4.显然，并查集最重要的就是find和union的过程。union的时候，我们要找到各自节点的根节点之后union，不能：

void union2(int x, int y) {
    if (find(x) != find(y)) {
        father[x] = y;
    }
}

这个错误现在看来有点愚蠢，但实际写代码的时候可能会疏忽，不容易发觉。

find的过程比union更复杂一些，为了达到更好的效果，我们希望进行路径压缩。那什么是路径压缩呢？如果你在这里有这样的问题，那就说明你没有好好看我开头给的链接，这会儿赶快去看看：如果你觉得翻到上面比较麻烦，这里我可以用飞雷神之术带你去那里。

在上面的模板中，我提供了两种find函数的写法。第一种比较中规中矩，先找到根，再进行路径压缩；第二种方法有递归的思想在其中，如何理解比较简单？你可以把find(father[x])当做是找到并查集的根源，我们可以生动一点，叫做“太祖”。带上了find()函数的头衔，经过递归的过程，就可以找到太祖。所以第二种方法的意思就是：如果你是太祖（x == father[x]，至于为什么这样就是太祖，那是因为并查集的初始化过程中我们给了每个节点“自立门户”的机会，在一顿合并之后，还能当老大的就是“真·太祖”了。），那就可以离开函数；如果不是，那么我们需要找到你的太祖，根据路径压缩的要求，我们希望找到的太祖就在你父节点的位置，那就是father[x] = find(father[x])啦，find(father[x])的find(·)就是一个黑匣子，把father[x]放进去，你就可以得到太祖，然后请他做你的父节点。这样一来，我们通过return的结果可以find到根节点也顺便进行路径压缩。是不是感觉这样的方法很简洁？如果不能很好地理解，那么还是用方法一，更加稳健。

至此，我们就分析完模板了，下面是力扣题。不过，在此之前，我还想再谈谈从并查集的设计思路上，我得到了什么样的启发？

并查集的使用其实是利用了father数组，设index为数组中的索引，那么就相当于构建了一个映射：father[·]，这样一个映射可以将index映射到index对应的根节点中。我们对于数组，传统的想法就是把一堆数字存在里面，然后通过索引把它们调出来使用，但在并查集这里，数组起到的作用更像是一个一元函数，具备映射的功能。如果可以从映射的角度理解并查集，应该能更容易明白其原理。

力扣547解答：

class DisjointSet {  // 本题使用并查集做
private:
    int father[200];  // 根据题目要求，n在1到200之间，可取200。
public:
    void init(int n) {
        for (int i = 0; i < n; i++) {  // 初始化
            father[i] = i;
        }
    }
    // int find(int x) { // 这个find可用
    //     int root = x;
    //     while (root != father[root]) {  // 寻根
    //         root = father[root];
    //     }
    //     int originalFather;
    //     while (x != root) {  // 路径压缩
    //         originalFather = father[x];
    //         father[x] = root;
    //         x = originalFather;
    //     }
    //     return root;
    // }
    
    int find(int x) { // 这个find也可用
        return x == father[x] ? x : father[x] = find(father[x]); // 已包含路径压缩和寻根
    }
    
    void union2(int x, int y) { // 合并。注意，在写合并的时候，分清根节点和当前节点的关系，容易错。
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            father[rootX] = rootY;
        }
    }
    bool same(int x, int y) { // 判断两个节点是不是同一个集合的
        return find(x) == find(y);
    }
    int getNums(int n) { // 得到省份数量。这里和模板不同，是根据这道题目增加的
        unordered_set res; // 一般来说，经常用set来计算并查集中集合的数量，也就是不交集（此处为省份）的数量
        for (int i = 0; i < n; i++) {
            res.insert(find(i)); // set中insert为插入方法。这里要插入节点的根，以此看有多少不同的集合
        }
        return res.size();
    }
};

class Solution {
public:
    int findCircleNum(vector>& isConnected) {
        int n = isConnected.size(); // n是矩阵大小。注意，这里矩阵肯定是对称矩阵，这有助于下面的优化
        DisjointSet UnionFind; // 并查集
        UnionFind.init(n); // 初始化
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (isConnected[i][j]) UnionFind.union2(i, j); // i城市和j城市有相连，那么就union起来 
            }
        }
        return UnionFind.getNums(n); // 得到结果
    }
};

这里插播一条广告：上面的代码可以在我的GitHub中查看。我的GitHub中还有很多别的力扣题目解答，如果你有兴趣，可以持续关注，我也将持续更新。如果你觉得不错，麻烦给我个Star~ღ( ´･ᴗ･` )比心。

我的力扣主页，GitHub主页，领英主页，知乎主页，欢迎大家有问题的时候进行交流。

这里写一点本题的注意事项：

1.bool same这个函数在这里用不到。

2.UnionFind.union2(i, j) 这里可能对于一些同学来说有些抽象，因为i和j就是两个数字，合起来代表的是矩阵中的一个位置，可能有点难理解两个数字union在一起是怎么回事。其实你可以这么看待这个问题：把i和j当成两个城市，比如i代表厦门，j代表西安，isConnected[i][j]就代表这两个城市是不是相连的。如果从具体事例了解，我相信有助于使用并查集的概念。

3.根据题目定义，这道题的矩阵肯定是一个对称矩阵，所以在第二层for循环上，可以进行些许优化；

4.最终得到结果用的是getNums函数，这个函数里面用了set（集合），这样的一个结构可以去重。当你把所有节点都处理过后，得到不同点对应的根节点。我们对根节点数量进行去重，可以得到省份数量。用set去重的题目在力扣里面挺多的，有的时候是一个不错的方法，比如力扣217和力扣287，在我的GitHub中也有对应题解：力扣217，力扣287。（是不是很神奇，一下子多解决两道题O(∩_∩)O哈哈~）这里也要注意一下，set是用insert方法添加元素，不像是vector用push_back，不同容器之间的不同用法应该及时整理区分，关于什么是容器，也可见我的GitHub，有相关内容。

至此，这道题目就算是做完了。怎么样？不难吧。

如果想要持续刷力扣，看题解，可以关注我的GitHub，我会持续更新。因为我也算是个新手，所以可能提出的很多值得注意的东西会与更多的新手有共鸣，欢迎大家指正与讨论！

在未来的日子里，希望与各位共同进步。这是我写的第一篇关于算法的博文，希望对你有一些帮助！

如果你觉得不错，烦请点赞或者GitHub加星（Star），不胜感谢！

最后是鸣谢环节：

1. 模板制作主要参考以下两个链接：

1.https://leetcode-cn.com/problems/number-of-provinces/solution/547-sheng-fen-shu-liang-bing-cha-ji-ji-c-qcj6/

2.https://leetcode-cn.com/problems/number-of-provinces/solution/python-duo-tu-xiang-jie-bing-cha-ji-by-m-vjdr/

2.感谢微信公众号“代码随想录”，这个公众号每天更新，对于力扣的题解和思路非常清晰，值得关注！

我们下次见~

结尾：

一些预告：

可能接下来有时间会写关于摩尔投票法的CSDN博文，这是一个非常有趣的内容。如果你按奈不住激动的心情，想要先行了解，那么可以直接在我的GitHub中查看，GitHub的更新肯定比CSDN要快得多~

至于未来还要做什么，写什么，现在还没有规划，应该会写自己感兴趣的，有意思的东西。如果想要成体系地看归类的题目，可以在我的GitHub中查看。