day7 8-牛客67道剑指offer-JZ74、57、58、73、61、62、64、65、把字符串转换成整数、数组中重复的数字
文章目录
- 1. JZ74 和为S的连续正数序列
-
- 暴力解法
- 滑动窗口(双指针)
- 2. JZ57 和为S的两个数字
- 3. JZ58 左旋转字符串
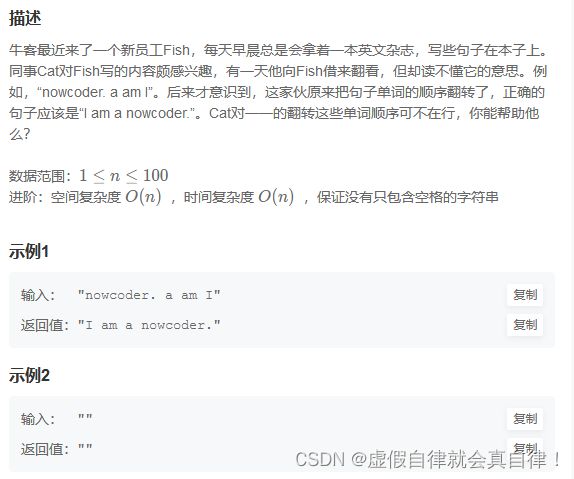
- 4. JZ73 翻转单词序列
- 5. JZ61 扑克牌顺子
- 6. JZ62 孩子们的游戏(圆圈中最后剩下的数)
-
- 迭代 模拟
- 递归 约瑟夫环问题 找规律
- 7. JZ64 求1+2+3+...+n
- 8. JZ65 不用加减乘除做加法
- 9. 把字符串转换成整数
- 10. 数组中重复的数字
-
- 哈希表
- 原地解法
1. JZ74 和为S的连续正数序列
暴力解法
class Solution {
public:
vector<vector<int> > FindContinuousSequence(int sum) {
if(sum == 0) return vector<vector<int>>{};
for(int i=1; i<sum; i++)
{
int temp = 0;
path.clear();
for(int j=i; j<sum; j++)
{
path.push_back(j);
temp += j;
if(temp == sum) result.push_back(path);
if(temp > sum) break;
}
//result.push_back(path);
}
return result;
}
vector<int> path;
vector<vector<int> > result;
};
class Solution {
public:
vector<vector<int> > FindContinuousSequence(int sum) {
//暴力解法 写法2
for (int n = sqrt(2 * sum); n >= 2; --n)
{
if (((n & 1) == 1 && sum % n == 0) || (sum % n * 2 == n))
{
vector<int> res;
//j用于计数,k用于遍历求值
for (int j = 0, k = sum / n - (n - 1) / 2; j < n; j++, k++)//注意看k的求法
res.push_back(k);
result.push_back(res);
}
}
return result;
}
vector<int> path;
vector<vector<int> > result;
};
滑动窗口(双指针)
class Solution {
public:
vector<vector<int> > FindContinuousSequence(int sum) {
//滑动窗口
int left = 1, right = 2, tempsum = 3;
while(left < right)
{
if(tempsum == sum)//保存结果
{
path.clear();
for(int i=left; i<=right; i++)
path.push_back(i);
result.push_back(path);
}
if(tempsum < sum)//窗口右边界外扩 右移
{
right++;tempsum += right;
}
else //tempsum > sum 窗口左边界右移;tempsum = sum 窗口左边界右移 开始下一轮子结果
{
tempsum -= left;//新的边界值
left++;
}
}
return result;
}
vector<int> path;
vector<vector<int> > result;
};
2. JZ57 和为S的两个数字
class Solution {
public:
vector<int> FindNumbersWithSum(vector<int> array,int sum) {
if(array.size() == 0) return vector<int>{};
// 滑动窗口 双指针 写法1
/*
int left = 0, right = array.size()-1;
while(left < right)
{
if(sum - array[left] == array[right])
{
result.push_back(array[left]);
result.push_back(array[right]);
break;
}
if(sum - array[left] < array[right]) right--;
else left++;
}
*/
// 滑动窗口 双指针 写法2
int left = 0, right = array.size()-1, tempsum = 0;
while(left < right)
{
tempsum = array[left] + array[right];
if(tempsum == sum)
{
result.push_back(array[left]);
result.push_back(array[right]);
return result;
}
else if(tempsum > sum) right--;
else left++;
}
return result;
}
vector<int> result;
};
3. JZ58 左旋转字符串
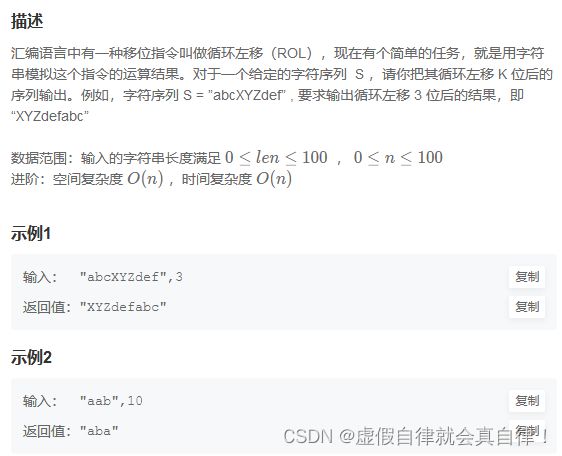
先局部反转 cbafedZYX,然后整体反转XYZdefabc
#include 4. JZ73 翻转单词序列
class Solution {
public:
string ReverseSentence(string str) {
if(str.size() <= 1) return str;
string result = "", temp = "";
for(int i=0; i<str.size(); ++i)
{
if(str[i] == ' ')//遇到空格 把temp和之前的结果拼接
{
result = ' ' + temp + result;//倒序拼接
temp = "";//更新 存下一个单词
}
else temp += str[i];//没有遇到空格 把整个字符串都存在temp中
}
if(temp.size()) // 如果temp还剩有单词 没有这一步的话示例1会返回" am a nowcoder."
result = temp + result;
return result;
}
};
5. JZ61 扑克牌顺子
- 排序,统计0的个数,统计所有相邻数字间隔总数。
- 如果0的个数 = 相邻数字间隔总数,就是顺子;如果出现对子,则不是顺子。
- 统计所有相邻数字间隔总数时,如果两个数字间隔为1,不计数。
class Solution {
public:
bool IsContinuous(vector<int>& numbers) {
if(numbers.size() < 5) return false;
sort(numbers.begin(), numbers.end());
int numOfZero = 0, numOfInner = 0;
//如果是连续的数 排序后 两两之间间隔为1
//比较0的个数 是否等于 统计的间隔长度 若相邻/间隔为1 视间隔长度为0
for(int i=0; i<numbers.size() - 1; i++)
{
if(numbers[i] == 0) numOfZero++;
else if(numbers[i] == numbers[i+1]) return false;//对子 不可能是顺子
else
{
numOfInner += numbers[i+1] - numbers[i] - 1;//相邻数的间隔长度为0 间隔长度累加
//numOfInner += numbers[i+1] - numbers[i] -1;//这里千万注意要减去1
}
}
if(numOfZero >= numOfInner) return true;
return false;
}
};
6. JZ62 孩子们的游戏(圆圈中最后剩下的数)
迭代 模拟
class Solution {
public:
int LastRemaining_Solution(int n, int m) {
if(n < 1 || m < 1) return -1;
vector<int> numbers(n,0);//标记哪个小朋友拿过礼物
int index = -1,step = 0, count = n;
while (count > 0)
{
index++;
if(index >= n) index = 0;//模拟环 从第一个小朋友开始
if(numbers[index] == -1) continue;
step++;//报数
if(step == m)
{
numbers[index] = -1;
step = 0;//下一个小朋友从头开始报数
count--;//已经有一个小朋友拿过礼物了 环中小朋友数量-1
}
}
return index;
}
};
递归 约瑟夫环问题 找规律

也就是说,从f(n-1, m)当前位置来看,f(n, m)在f(n-1, m)的后m个位置。n个数字中最后剩下的数字,即去掉的数字为(m-1)%n,下一次报数是从第 m%n 个数字开始。因此,f(n-1) 和 f(n)的关系如下:
| f(n-1) | f(n) |
|---|---|
| 0 | m%n |
| 1 | (m+1)%n |
| … | … |
| n-2 | (m-2)%n |
两种写法
#include 7. JZ64 求1+2+3+…+n

不能用if、switch、?:等操作时,利用逻辑与的短路特性实现递归终止,也就是通过判断n是否为0来控制递归是否终止。
n递减,并且通过递归实现倒序累加和。当n = 0时,递归结束;n > 0时,递归,倒序累加求和。因此判断条件是 (n > 0) && ((result += Sum_Solution(n-1)) > 0);
class Solution {
public:
int Sum_Solution(int n) {
int result = n;
(n > 0) && ((result += Sum_Solution(n-1)) > 0);
return result;
}
};
8. JZ65 不用加减乘除做加法


两个数异或:相当于每一位相加,而不考虑进位,产生非进位的加和结果;
两个数相与,并左移一位:相当于求得进位;
将上述两步的结果相加,什么时候进位制为0也就说明两个数相加到了最终点,也就计算结束了。
5-101,7-111
第一步:相加各位的值,不算进位,得到010,二进制每位相加就相当于各位做异或操作,101^111。
第二步:计算进位值,得到1010,相当于各位做与操作得到101,再向左移一位得到1010,(101&111)<<1。
第三步重复上述两步, 各位相加 010^1010=1000,进位值为100=(010&1010)<<1。
继续重复上述两步:1000^100 = 1100,进位值为0,跳出循环,1100为最终结果。
class Solution {
public:
int Add(int num1, int num2) {
//位运算 迭代
int add = num2;// add表示进位值
int sum = num1; // sum表示总和
while(add != 0)
{
int temp = sum ^ add;// 将每轮的无进位和与进位值做异或求和
add = (sum & add) << 1;// 进位值是用与运算产生的
sum = temp;// 更新sum为新的和
}
return sum;
}
};
9. 把字符串转换成整数

要注意的两点,1.越界处理,2.正负号个数处理,越界处理用下面这种写法的时候,怎么改都只能通过95.5%的用例,最后还有两组用例没过。换成练习模式才知道原来是过不了“±5”这种例子,真的无语,加了一个统计正负号个数的判断。
#include
index++;
}
return result;
}
};
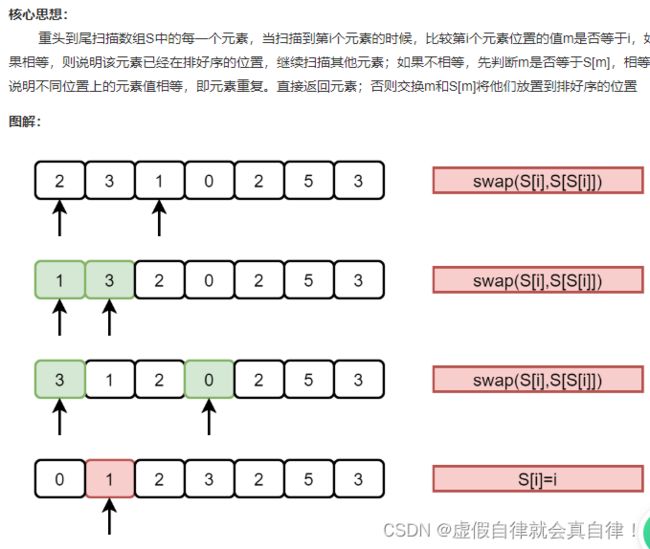
10. 数组中重复的数字
哈希表
使用了循环,循环次数为数组大小,时间复杂度为O(N)。引入额外的集合空间,空间复杂度为O(N),最坏的情况是数组中的元素都不重复。
- 用map
#include - 用vector,降低内存复杂度
#include 原地解法
- 如果numbers[index] = index,第index个位置的元素也可以用numbers[numbers[index]]来表示
- 使用了循环,循环次数为数组大小,时间复杂度为O(N)。没有引入额外的集合空间,空间复杂度为O(1)
#include