【Neural Style Transfer】 Fast Neural Style
上周写了深度学习与艺术——画风迁移 Neural Style的文章,这周就来聊一聊Fast Neural Style,从名字可以看出,Fast Neural Style的最大的特色就是快,也就是说如果再优化网络配置ok的话完全可以达到落地应用的地步了。
0 回顾Neural Style
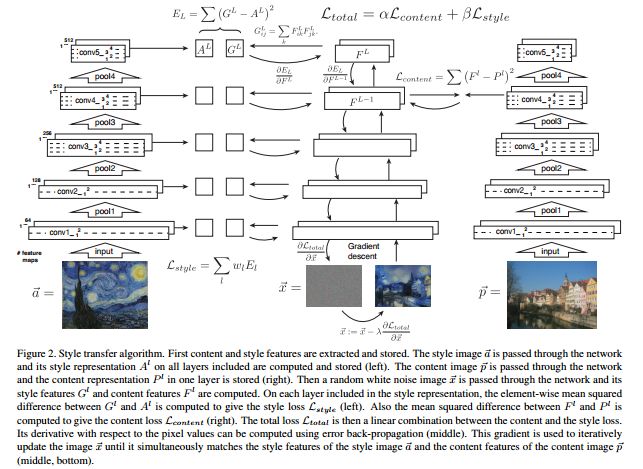
在聊Fast Neural Style之前,我们先来回顾一下Neural Style,其实用Gatys的一张图就可以解释Neural Style在做什么(如下图)。Neural Style是Gatys提出的不同于传统风格迁移的一种新方式,它利用卷积神经网络可以完成不同图像之间的风格迁移,使人们产生一种视觉上的“错觉”。
1 Fast Neural Style
Fast Neural Style论文:Perceptual Losses for Real-Time Style Transfer and Super-Resolution
论文链接:https://arxiv.org/abs/1603.08155
1.1 Fast Neural Style的两个任务
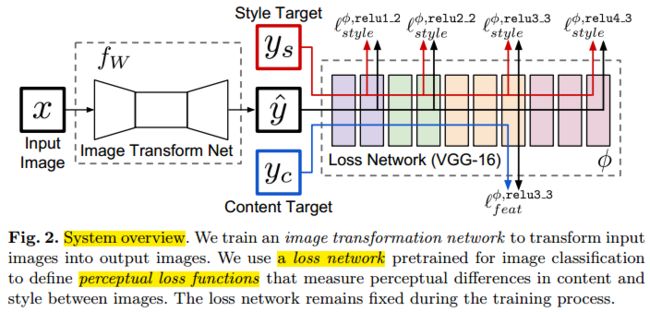
Fast Neural Style主要是有两个任务:风格迁移任务和单张图像的超分辨率任务。 风格迁移任务同Neural Style相同,将图像A的风格前已在图像B的内容上,生成具有图像A风格且与图像B内容相同的图像C;单张超分辨率任务指的是从输入的低分辨率图像生成一张高分辨率的图像。Fast Neural Style的体系含有两部分,分别是图像迁移网络(image transformation network , f W f_W fW) 和损失网络(a loss network , ϕ \phi ϕ) ,如下图所示;
1.2 Image Transform Net
基本的结构是用了五个残差模块;没有池化层,用的是卷积步长>1和卷积步长<1的卷积来进行下采样和上采样;激活函数用的书Relu激活函数;卷积核的大小是9x9和3x3;
【不同的任务输入图像输出图像的尺寸是不同的】
对于风格迁移任务:input——256x256x3;output——256x256x3;
对于超分辨率任务:input——(288/f)x(288/f)x3;output——288x288x3;
【Downsampling下采样和Upsampleing上采样】
对于风格迁移任务,网络先使用的是步长为2的卷积残差块去下采样,再使用2层卷积层使用步长为0.5的上采样。虽然输入和输出具有相同的大小,但先下采样后再上采样对网络仍有益处:一是可以减少计算量,二是可以有益于可接受的感受野。
1.3 Loss Network
在我们要了解loss network之间,我们先来看一下损失函数(要保证损失函数可微可导可回传)。其实我们可以这样理解损失函数:之所以有损失函数,是因为我们生成的和真实存在的或者是ground truth之间存在着差异,我们要找到一种数学上的方式来描述这种差异,并且可以在迭代和优化中不断缩小这种差异,所以损失函数在一个网络中是十分重要的。网络用两个感知损失函数定义了不同图像之间的高水平感知和语义差距;并且用了在ImageNet数据集上预训练的VGG16的网络。
【特征重构损失函数】Feature Reconstructions Loss
特征重构的意义不在于逐个像素点的match,而是想要得到特征的相似,也就是说我们要在Feature Map上有一种关系,假设我们在j层上的输出Feature Map的大小是: C j ∗ H j ∗ W j C_j * H_j *W_j Cj∗Hj∗Wj,那么,我们用欧氏距离来衡量这种特征相似性,如下式:
l f e a t ϕ , j ( y ^ , y ) = 1 C j H j W j ∣ ∣ ϕ j ( y ^ ) − ϕ j ( y ) ∣ ∣ 2 2 (2) l^{\phi , j}_{feat}(\hat{y},y) = \frac{1}{C_jH_jW_j} || \phi_j(\hat{y})-\phi_j({y}) ||_2^2 \tag2 lfeatϕ,j(y^,y)=CjHjWj1∣∣ϕj(y^)−ϕj(y)∣∣22(2)
(个人理解) 在特征图上的相似性可以看做找到了像素相似性和语义相关性的平衡,是我们训练的模型不会看起来非常像(像素值非常接近),不会看起来一点儿也不像(基本特征都没有学习到)。
【风格重构损失函数】Style Reconstruction Loss
我们希望训练的模型除了关注特征上的相似性以外,还要关注颜色、纹理、普通模式等等风格上的相似性,所以提出了Style Reconstruction Loss(Gatys)。我们在j层上的Feature map用Gram矩阵来描述这种差距,如下式(3);那么我们就可以得到所有层的风格重构损失了,如下式(4);
G j ϕ ( x ) c , c ′ = 1 C j H j W j ∑ h = 1 H j ∑ w = 1 W j ϕ j ( x ) h , w , c ϕ j ( x ) h , w , c ′ (3) G_j^{\phi}(x)_{c,c'} = \frac{1}{C_jH_jW_j} \sum_{h=1}^{H_j} \sum_{w=1}^{W_j} \phi_j(x)_{h,w,c} \phi_j(x)_{h,w,c'} \tag3 Gjϕ(x)c,c′=CjHjWj1h=1∑Hjw=1∑Wjϕj(x)h,w,cϕj(x)h,w,c′(3)
l s t y l e ϕ , j ( y ^ , y ) = ∣ ∣ G j ϕ ( y ^ ) − G j ϕ ( y ) ∣ ∣ 2 2 (4) l^{\phi,j}_{style}(\hat{y},y) = ||G_j^{\phi}(\hat{y})-G_j^{\phi}({y})||^2_2 \tag4 lstyleϕ,j(y^,y)=∣∣Gjϕ(y^)−Gjϕ(y)∣∣22(4)
1.4 Simple Loss Functions
除了定义了感知函数,我们还定义了两个简单的只取决于低层次像素信息的损失函数,分别是像素损失(Pixel Loss) 和 全变正则化(Total Variation Regularization, l T V ( y ^ ) l_{TV} ( \hat{y} ) lTV(y^))。
2 实验 Experiments
如上所知,Fast Neural Style主要是有两个任务:风格迁移任务和单张图像的超分辨率任务,我们来看一下都进行了些什么样的实验。
2.1 风格迁移任务 Style Transform
我们要得到一张具有A图像内容(下称图像 y c y_c yc)具有B图像风格(下称图像 y s y_s ys)的图像C(也就是我们的生成目标 y ^ \hat{y} y^),这就要求我们的图像C有了两个目标targets—— y c y_c yc和 y s y_s ys;基于两个目标要求我们的损失函数要在特征重构 l f e a t l_{feat} lfeat和风格重构 l s t y l e l_{style} lstyle上都要有所涉及,作者还巧妙的加了一个正则项 l T V l_{TV} lTV,如下式:
y ^ = arg min y λ c l f e a t ϕ , j ( y , y c ) + λ s l s t y l e ϕ , J ( y , y s ) + λ T V l T V ( y ) (5) \hat{y}= \mathop {\arg\min}_{y} \ \ \lambda_cl_{feat}^{\phi,j}(y,y_c)+\lambda_sl_{style}^{\phi,J}(y,y_s)+\lambda_{TV}l_{TV}(y) \tag5 y^=argminy λclfeatϕ,j(y,yc)+λslstyleϕ,J(y,ys)+λTVlTV(y)(5)
其中, λ c \lambda_c λc, λ s \lambda_s λs和 λ T V \lambda_{TV} λTV是超参数。具体训练细节参见论文。在结果(下图)中我们可以看到,训练过的风格迁移网络有一种对于图像语义内容的意识。比如说图中背景部分比较杂乱没有办法辨认出来而前景物体效果较好——作者也因此做了及时:作者认为预训练的VGGNet-16网络对于人类或者动物具有选择性的特征。
在速度方面Fast Neural Style也有一定的优势,处理512x512的图像可以达到20FPS,这也是图像风格迁移有机会应用到实际应用和视频中。
2.2 单张图像的高分辨率任务 Single-Image Super-Resolution
在单张图像的高分辨率中,我们的任务就是从一张输入的低分辨率的图像生成一张高分辨率的图像。这并不是有统一解的问题,因为使用的生成方法不同,生成的高分辨率的图像是不同的。
我们只关注与x4倍和x8倍的分辨率问题,因为更大的分辨率要有更多的语义推理。为了克服低分辨率转高分辨率的问题,我们不再使用逐像素的损失,而使用特征重构损失 l f e a t l_{feat} lfeat。用于评价超分辨率问题的传统评估度量是——PSNR和SSIM,虽然我们的网络并不旨在这两个评估度量都取得优异效果,但这也从侧面反映了我们训练像素损失和重构损失的可靠性。
在超分辨率的任务里,我们用了SRCNN的三层卷积层网络,用于在ILSVRC 2013检测数据集的33×33块上最小化每个像素的损失。SRCNN没有训练×8倍的超分辨率,所以我们只能在×4倍上对其进行评估。和其他方法相比,我们训练的特征重构模型在重构尖锐的边缘和具体的细节表现了良好的性能,虽然有可能会在PSNR和SSIM上有一定的影响。