学习总结7/17-19

目录

动态规划算法思路

1、确定状态

2、状态转移方程

3、初始条件和边界情况

4、计算顺序（for循环）

frog_stone D题

frog_stone+k C题

二分子序列_ A题

基因片段_M题

暑假最大快乐值_B题

01背包/完全背包

 cut_ribbon E题

memset函数用法

---

动态规划算法思路

1、确定状态

        解动态规划问题的时候需要开一个数组，数组的每一个元素a【i】或者a【i】【j】代表什么

        确定状态需要的两个意识

                一、最后一步

                二、子问题

                子问题是由原问题化简而来，意思与原问题相同，规模相较原问题变小

2、状态转移方程

        根据题意写递归方程

        虽然写递归方程但是不建议用递归，因为

                递归解法做了很多重复计算，时间复杂度直接指数级，效率低下

                如何避免？1、将计算结果保存 2、改变计算顺序

        如果用方法1，保存计算结果，可以用哈希表来保存

        方法2，改变计算顺序，也就是这次动态规划的核心内容（详细情况我会边做题边分析

3、初始条件和边界情况

        初始条件：用转移方程算不出来的需要手工定义

        边界情况：数组不要越界

4、计算顺序（for循环）

        大部分动态规划问题都是从小到大计算，二维数组就是从上到下从左到右计算

        因为最后需要得到的值需要前面值的相加得到，如果不从小到大，将会取不到值

光看这个会比较抽象，做题时我会在根据题意代入相关步骤来解题

frog_stone D题

这个题呢可以说是很规范的dp入门题了

理一下思路哈 如图，如果用递归，要重复计算好多数，时间复杂度度贼拉高

 要是用动态规划的话，改变计算顺序，从小到大计算青蛙在第i个台阶跳的最优方法

ans【i】存储该是由两种方式的较小值

ans[i]=max(ans[i-1]+abs(a[i-1]-a[i-2]),ans[i-2]+abs(a[i-1]-a[i-3]));

改变计算顺序，从小到大计算青蛙在第i个台阶跳的最优方法，这样就能避免重复计算

 这一题需要注意n的范围  2≤N≤105

ac核心代码（注释是为了让我写出正确的角标

注意搞清楚题意，要求求最小消耗，用min函数

int bp()
{
    ans[0]=0;
    ans[1]=0;
    ans[2]=abs(a[1]-a[0]);
    //ans[3]=max(ans[2]+a[2]-a[1],a[2]-a[0]);
    //ans[4]=max(ans[3]+a[3]-a[2],ans[2]+a[3]-a[1]);
    for(int i=3;i

frog_stone+k C题

 在上一题的基础上多了一个条件，加一个循环即可，但是要注意的蛮多

1、得考虑k=1的情况

        直接每两步的差值之和

2、在循环里得考虑i-j>0

        因为如果k比n大，循环k的时候要是一直循环，很费时间并且数组都不存在了还搁那循环，会TLE哦

3、mmin尽量开大一点

ac核心代码

int dp()
{
    ans[0]=0;
    ans[1]=0;
	ans[2]=abs(h[1]-h[0]);
    int mmin;
    for(int i=3;i<=n;i++){
    	mmin=INF;
    	for(int j=1;j<=k && i-j>0;j++){
    		int temp=ans[i-j]+abs(h[i-1]-h[i-j-1]);
    		if(temp

下次弄这样的我输入一定要从1开始，看花眼了我真的

二分子序列_ A题

 二分类相关的题无非就是两点

一个是二分区间

这个题第一次二分区间，r是这段序列的最大值，l是这段序列的和

一个是check函数应该怎么写

因为一般都是，二分的格式写在主函数，check函数作为判断二分区间的条件

就像这样

while(r>l){
        //二分
            if(check(mid))
                r=mid;
            else
                l=mid+1;
            mid=(r+l)/2;
        }

这一题的check函数，因为题意得子序列一定是相互连接的，而且主要是要m个子序列的最大最小值（？表达好奇怪）

反正就是要使得每个子序列和均不超过某个值X，求X的最小值

ac代码

bool check(int mid)
{
    int cnt=1,sum=0;
    for(int i=0;i

基因片段_M题

 这一题也是个动态规划，按照动态规划的步骤来像吧

1、确定状态

a 和b是两个序列，将 a 和 b 的最长公共子序列记为ans(a.b)

a={a1,a2,....an};

b={b1,b2,....bm};

我们需要找到a 和b中最长的公共子序列。而要找a和b的ans，首先考虑a的最后一个元素和b的最后一个元素

1）如果 an=bm，即a的最后一个元素与b的最后一个元素相同，这说明该元素一定位于公共子序列中。因此，现在只需要找：ans(an-1，bm-1)

ans(an-1，bm-1)就是原问题的一个子问题。

2）如果an != bm，即a的最后一个元素与b的最后一个元素不相同，这说明该元素（a中最后一个或者b中最后一个）不位于公共子序列中，所以

它产生了两个子问题：ans(an-1，bm) 和 ans(an，am-1)

2、状态转移方程

由上面的分析可得，我们将原问题化为了3个子问题，现在这个状态就可以用状态转移方程

ans(an-1，bm-1)

ans(an-1，bm)

ans(an，am-1)

3、初始条件和边界条件

边界条件就在输入的字符串范围内就好了，这题没什么特别要求

4、改变顺序

但是嘞，之前也提过，用递归会重复计算导致这个题目的时间复杂度为指数级，巨慢

那么我们就可以通过改变顺序，从a1开始计算

这道题目需要用到一个ans【】【】二维数组存储ai，bj的最长公共子序列

                             ans【i-1】【j-1】 ，a【i-1】==b【j-1】

ans【i】【j】={   

                            max（ ans【i】【j-1】，ans【i-1】【j】）    ，a【i-1】！=b【j-1】

ac核心代码

int bp()
{
    memset(ans,0,sizeof(ans));
    for(int i=1;i<=strlen(a);i++)
        for(int j=1;j<=strlen(b);j++){
            if(a[i-1]==b[j-1]){
                ans[i][j]=ans[i-1][j-1]+1;
            }
            else{
                ans[i][j]=max(ans[i-1][j],ans[i][j-1]);
            }
        }
    return ans[strlen(a)][strlen(b)];
}

暑假最大快乐值_B题

好，这题又是个动态规划，我一开始的思路是写了个结构体变量存储事件，用一个flag来标记牛子爷选择干嘛，但是代码很长很花眼睛不说，还总是有bug，并且我不晓得我的bug在哪，怎么看怎么对，好，bug没解决，我又发现我思路错了

好，换个思路，我发现，可以，用二维数组！

一开始输入就存二维数组里，就不用结构体变量了，然后和上面那题有点相似吧，具体的慢慢再分析，搞！

 用二维数组真的很简单内

for(int i=0;i<3;i++)
		ans[0][i]=hap[0][i];
		
	for(int i=1;i

 用下面这组数（右）举个例子，那么最后存在ans数组（左）里的会是

3

10 40 70                                10                                        40                                         70

20 50 80                      20+max(40,70)=90      50+max(10,70)=120         80+max(10,40)=120

30 60 90                     30+max(110,120)=150     60+max(90,120)=180      90+max(120,90)=210

 最后再比较ans数组最后一行的三个数，输出最大的那个数，得到最大快乐值

做E题，我反正是没思路，一C，说可以用完全背包来写

然后我就去看了看01背包，完全背包的思路，也都是dp动态规划算法

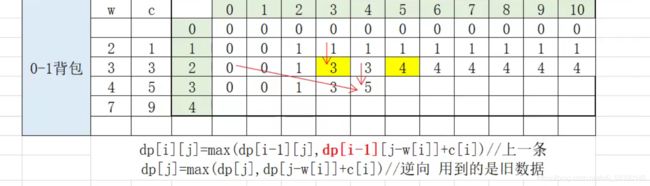
01背包/完全背包

一般是做背包问题，背包问题首先想到的是用贪心来写，但是其实用动态规划也可以写，贪心不一定会得到最优解

 定义一个bp【i】【j】二维数组，行存储物品，列存储容量，bp【i】【j】的值为价值

物品重量用w【i】表示，价格用c【i】表示

可以这样表示（b站up主 睿爸信奥 那截的，我懒得自己做了） 

 还能优化空间，就是直接dp【j】弄一个一维数组，压缩空间

不过这样的话，就得从后往前，逆序

完全背包的话

 cut_ribbon E题

这一题就是可以用的完全背包来解决

把价值看做是1，也就是切出的丝带加一条

背包容量就可以看做丝带长度

物品价值看做丝带可允许被切的长度

有个点呢是bp数组需要初始值赋值为一个很小的负数（我自己敲的时候全都赋为0，答案错了）

因为一直一直错误我就去搜了题解，题解也就一句“要是不这么赋的话可能背包没装满”，我看不懂并且大为震撼（现在也不懂有大佬的话求指点！！）

然后嘞我就直接一个

const int INF=-99999999；

memset（dp，INF，sizeof（dp））；

错了，一直错，

我还以为是我核心代码的问题，一直在和题解的答案对比，检查了好久也没什么错的，然后，试了一下memset改成for循环赋值，妹想到问题就会是出在这

我去c了一下memset，找到了原因

memset函数用法

作用是将数字以单个字节逐个拷贝的方式放到指定的内存中去

因为char是1字节，memset是按照字节赋值的，相当于把每个字节都设为那个数，所以char型的数组可赋任意值

也就是说memset一般用来赋值函数为0或者-1，

我们可以用memset(a,127,sizeof(a));  实现将数组里的全部元素初始化为一个很大的数，在最短路径问题以及其他很多算法中都是需要用到的。初始化int类型的数组也可以使用127这个数值

可以用memset(a,128,sizeof(a));  将数组初始化为一个很小的数

ac代码

#include
#include
#include
#include
#include
using namespace std;
const int INF = -9999;

int main()
{
    int n,a[3];
    cin>>n;
    for(int i=0;i<3;i++)
        cin>>a[i];
    int dp[4005];
    memset(dp,INF,sizeof(dp));
    dp[0]=0;
    for(int i=0;i<3;i++){
        for(int j=a[i];j<=n;j++){
            dp[j]=max(dp[j],dp[j-a[i]]+1);
        }
    }
    cout<