pytorch 基本操作(五)——激活函数和梯度
激活函数和梯度
- 激活函数
-
- Sigmod激活函数
- Tanh
- ReLu
- softmax
- Loss Function
-
- loss
- L2-norm
- 梯度
-
- autograd
- 向后传播 backward
- Softmax举例
激活函数
激活函数(Activation Function),就是在人工神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。引入激活函数是为了增加神函数模型的非线性。如果不用激活函数,单纯利用线性去做预测的话,这样损失函数的现实意义是不明显也是不合理的。
Sigmod激活函数
其中一个函数就是Sigmod函数。
f ( x ) = σ ( x ) = 1 1 + e − x f(x) = \sigma(x) = \frac{1}{1+e^{-x}} f(x)=σ(x)=1+e−x1
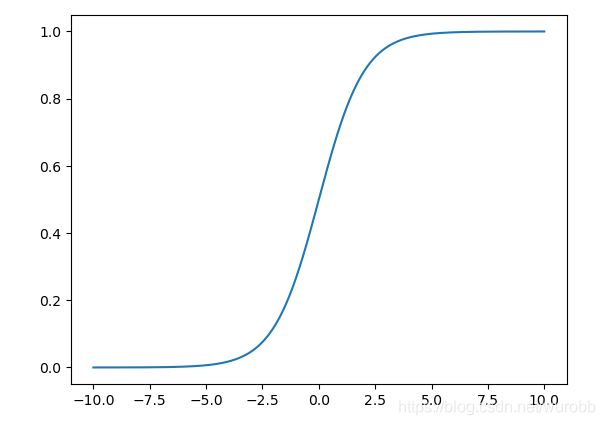
绘制一下Sigmod函数的图像,可以看出它是一条比较平滑的曲线,f(x)的取值范围在0到1之间。
import matplotlib.pyplot as plt
import torch
sigmod_x = torch.linspace(-10,10,1000)
sigmod_y = 1/(1+torch.exp(-sigmod_x))
plt.plot(sigmod_x,sigmod_y)
plt.show()
Tanh
Tanh是另一个激活函数,表达式如下。
f ( x ) = t a n h ( x ) = e x − e − x e x + e − x f(x) = tanh(x) = \frac{e^x -e^{-x}}{e^x +e^{-x}} f(x)=tanh(x)=ex+e−xex−e−x
其实他是Sigmod函数的一个变形。
f ( x ) = t a n h ( x ) = 2 S i g m o d ( 2 x ) − 1 f(x) = tanh(x) = 2Sigmod(2x)-1 f(x)=tanh(x)=2Sigmod(2x)−1
同样我们可以看一下tanh函数的长什么样子,可以看出它是一条比较平滑的曲线,与sigmod函数变化趋势比较相似,f(x)的取值范围在-1到1之间。
tan_x = torch.linspace(-10,10,1000)
tanh_y = (torch.exp(tan_x)-torch.exp(-tan_x))/(torch.exp(tan_x)+torch.exp(-tan_x))
ReLu
ReLu函数也是一个比较常用的激活函数,有利于解决梯度爆炸的问题,表达式如下。
f ( x ) = { 0 , f o r x < 0 x , o t h e r s f(x) = \begin{cases}0,\ for\ x<0\\x,\ others\end{cases} f(x)={0, for x<0x, others
函数很简单,就不画了,自己想象吧。
softmax
数学表达式如下所示:
S ( x i ) = e x i ∑ e x i S(x_i) = \frac{e^{x_i}}{\sum e^{x_i}} S(xi)=∑exiexi
这是一个以 x i x_i xi取值来赋予其不同概率权重的函数。
Loss Function
损失函数就是来记录你的模型损失了多少信息的函数,这里分为几种。
最大的分类就是MSE,MSE中文名是均方误差,是指模型预测值和真实值之间差的衡量函数,在这里用 y y y代表真实值,有时也称为label值。用 y ^ \hat y y^代表模型预测值,那么MSE其中一个形式loss表示如下:
loss
l o s s = ∑ [ y − ( y ^ ) ] 2 loss = \sum[y-(\hat y)]^2 loss=∑[y−(y^)]2
在这里我们的mse函数为:
m s e = ( 1 − w ∗ 1 ) 2 w h e n w = 3 , m s e = 4 mse = (1 - w*1)^2 \\ when\ w = 3, mse = 4 mse=(1−w∗1)2when w=3,mse=4
x = torch.ones(1)
w = torch.full([1],3.)
mse = torch.nn.MSELoss(reduction='mean')
mse(torch.ones(1),x*w)
# 输出:tensor(4.)
另一种表达方式如下:
L2-norm
L 2 − n o r m = ∣ ∣ y − y ^ ∣ ∣ 2 L2-norm = ||y-\hat y||_2 L2−norm=∣∣y−y^∣∣2
梯度
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
这里插入一个概念,在机器学习和深度学习中,我们的目标是将损失函数最小化,这时候我们要获得的就是 m i n L o s s min\ Loss min Loss 的值和其对应参数,这时候常用的方法就是梯度下降法,可以参考一下我的上一篇《梯度下降——R语言》文档,python代码可以点击该链接python代码的20-23文档。
autograd
pytorch 可以进行求导操作,这里我们以mse-loss函数举例。
在这里我们的mse函数为:
m s e = ( 1 − w ∗ 1 ) 2 ∴ d m s e d w = 2 ( 1 − w ) ( − 1 ) w h e n w = 3 , d m s e d w = 4 mse = (1 - w*1)^2 \\\therefore \frac{\pmb dmse}{\pmb d w} = 2(1-w)(-1) \\ when\ w = 3, \frac{\pmb dmse}{\pmb d w} = 4 mse=(1−w∗1)2∴dddwdddmse=2(1−w)(−1)when w=3,dddwdddmse=4
在pytorch中需要求导的函数需要对其进行设置,在张量里用requires_grad = True设置,也可以使用.requires_grad_().
w = torch.full([1],3.,requires_grad = True)
mse = torch.nn.MSELoss(reduction='mean')
mse1 = mse(torch.ones(1),x*w)
torch.autograd.grad(mse1,w)
# 输出::(tensor([4.]),)
这和我们求得的梯度一模一样了。
向后传播 backward
.backward 会自动计算所有的标记有需要梯度的tensor的梯度信息。
w = torch.full([1],3.,requires_grad = True)
mse = torch.nn.MSELoss(reduction='mean')
mse1 = mse(torch.ones(1),x*w)
mse1.backward()
w.grad
# 输出::(tensor([4.]),)
与autograd的计算结果一样。
这样就大致介绍了pytorch中的导数和梯度的一些概念。
Softmax举例
import torch
import torch.nn.functional as F
a = torch.rand(3)
a.requires_grad_()
p = F.softmax(a, dim = 0)
torch.autograd.grad(p[1],[a],retain_graph = True)
# (tensor([-0.1392, 0.2247, -0.0855]),)
p[1].backward(retain_graph = True)
a.grad
# tensor([-0.1392, 0.2247, -0.0855])