代码随想录算法训练营第十八天| 513.找树左下角的值,112.路径总和 ,113.路径总和 II,106.从中序与后序遍历序列构造二叉树(值得二刷),105.从前序与中序遍历序列构造二叉树
513.找树左下角的值
递归法+回溯
寻找最大深度,当遇到叶子节点,要判断一下是否需要更新最大深度
//递归法,找最大深度
private int Deep=-1;
private int value=0;
public int findBottomLeftValue(TreeNode root) {
value=root.val;
findLeftValue(root,0);
return value;
}
public void findLeftValue(TreeNode root,int deep){
if(root==null){return;}//终止条件
if(root.left==null&&root.right==null){//当遇到叶子节点的时候,就需要统计一下最大的深度了,所以需要遇到叶子节点来更新最大深度。
if(deep>Deep){
value=root.val;
Deep=deep;
}
}
if(root.left!=null){
deep++;//深度+1;
findLeftValue(root.left,deep);
deep--;//回溯
}
if(root.right!=null){
deep++;
findLeftValue(root.right,deep);
deep--;}
}迭代法,也叫BFS,返回每一层最左边的元素(也是第一个元素即i=0时)
class Solution {
//迭代法,返回最后一层最左边的元素
public int findBottomLeftValue(TreeNode root) {
Queue queue=new LinkedList<>();
queue.offer(root);//向队尾压入元素
int res=0;
while(!queue.isEmpty()){
int size=queue.size();
for(int i=0;i 112.路径总和
112. 路径总和
思路:
递归法,一条路径一条路径走,如果某一条路径走完了发现不符合要求就需要从当前节点不断回溯
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
//递归方法判断有没有哪一条路径对于目标和
if (root == null){return false;}
return traversal(root, targetSum - root.val);
}
boolean traversal(TreeNode root, int count) {
if(root.left==null&&root.right==null&&count==0){return true;}
if(root.left==null&&root.right==null){return false;}
if(root.left!=null){
count-=root.left.val;
if(traversal(root.left,count)){return true;}//递归当前节点的左节点
count+=root.left.val;//如果没有走上面的if语句,那么就会执行到这里。我们就需要把root.left.val加回来
}
if(root.right!=null){
count-=root.right.val;
if(traversal(root.right,count)){return true;}//递归到叶子节点然后找到了count为0的路径
count+=root.right.val;
}
return false;
}
}113.路径总和II
113. 路径总和 II
思路:递归+回溯,和112.路径总和 思路一致,
1.确定递归函数dfs的参数和返回值
2.确定终止条件:当前节点的左右孩子为空且计数器count为0
3.递归逻辑:遍历当前节点的左子树和右子树
class Solution {
//递归法+回溯
//需要搜索整棵树,找到符合条件的路径
List> res=new ArrayList<>();
List path = new LinkedList<>();
public List> pathSum(TreeNode root, int targetSum) {
int count=targetSum;
if(root==null){return res;}
path.add(root.val);
dfs(root,count-root.val);
return res;
}
void dfs(TreeNode root,int count){
if(root.left==null&&root.right==null&&count==0){
res.add(new ArrayList<>(path));//找到了符合要求的路径,加入到结果集res中
return;
}
if(root.left!=null){
path.add(root.left.val);
count-=root.left.val;
dfs(root.left,count);
count+=root.left.val;//回溯
path.remove(path.size()-1);//回溯
}
if(root.right!=null){
path.add(root.right.val);
count-=root.right.val;
dfs(root.right,count);
count+=root.right.val;
path.remove(path.size()-1);
}
}
} 106.从中序与后序遍历序列构造二叉树(值得二刷)
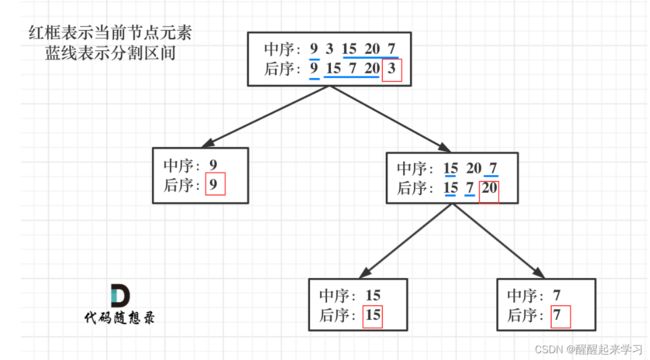
如何根据两个顺序构造一个唯一的二叉树,就是以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来再切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。流程如图
代码思路:
这里在找rootValue的时候写成postorder.length-1导致栈溢出,
1.先找到后序遍历数组的最后一个元素(就是根节点)
2.将根节点作为中序数组的分割点以此将其划分为左中序和右中序
3.切割完中序数组和后序数组后划分区间,再对划分的区间dfs,区间都是左闭右开(可根据题目示例进行分析一下)
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
if (inorder.length == 0 || postorder.length == 0) return null;
// 叶子节点
return dfs(inorder, postorder,0,inorder.length,0,postorder.length);
}
public TreeNode dfs(int[] inorder, int[] postorder, int inorderStart, int inorderEnd,int postorderStart, int postorderEnd){
if(postorderStart == postorderEnd){
return null;
}
//1.找到后序遍历数组最后一个元素(就是树的根节点),作为中序数组的分割点
int rootValue = postorder[postorderEnd - 1];//这里写成postorder.length-1导致栈溢出
TreeNode root = new TreeNode(rootValue);
// 找到中序遍历的切割点
int delimiterIndex;
for(delimiterIndex=inorderStart;delimiterIndex105.从前序与中序遍历序列构造二叉树
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder.length==0||inorder.length==0){return null;}
return dfs(preorder,inorder,0,preorder.length,0,inorder.length);
}
public TreeNode dfs(int[] preorder, int[] inorder,int preorderBegin,int preorderEnd,int inorderBegin,int inorderEnd){
if(preorderBegin==preorderEnd){return null;}
int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0
TreeNode root = new TreeNode(rootValue);
if (preorderEnd - preorderBegin == 1) return root;
//在中序数组找到中序数组的分割点
int delimiterIndex;
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// 切割中序数组
// 中序左区间,左闭右开[leftInorderBegin, leftInorderEnd)
int leftInorderBegin=inorderBegin;
int leftInorderEnd=delimiterIndex;
int rightInorderBegin=delimiterIndex+1;
int rightInorderEnd=inorderEnd;
//切割前序数组
int leftPreorderBegin=preorderBegin+1;
int leftPreorderEnd=preorderBegin+1+delimiterIndex-leftInorderBegin;
int rightPreorderBegin=leftPreorderEnd;
int rightPreorderEnd=preorderEnd;
root.left=dfs(preorder,inorder,leftPreorderBegin,leftPreorderEnd,leftInorderBegin,leftInorderEnd);
root.right=dfs(preorder,inorder,rightPreorderBegin,rightPreorderEnd,rightInorderBegin,rightInorderEnd);
return root;
}
}