HoudiniVex笔记_P20_SolverBascis解算基础

原视频：https://www.youtube.com/playlist?list=PLzRzqTjuGIDhiXsP0hN3qBxAZ6lkVfGDI
Bili：Houdini最强VEX算法教程 - VEX for Algorithmic Design_哔哩哔哩_bilibili

Houdini版本：19.5

1、什么是解算器

Houdini的解算器的作用是计算物体（刚体、线缆、布料表面、流体等）的模拟行为。

下面是来自用户@qq_39239990的理解，

解算器是基于帧的反馈处理，将当前帧的结果用于下一帧计算，以此循环，

解算器节点，双击节点后如下所示，节点第一个输入将用于解算的初始值， 
因此解算器的结果不能连接新求解器的第一个输入，可连其它输入，

eg.下面用解算器对点进行移动。
①如下图创建节点，其中的圆circle节点方向设置为X-Z平面或随意，

②在类型为Points的move节点写入代码：@P.y += 0.01;
③结果：图略，点击播放按钮，点将向Y轴移动。

2、基础变换

用解算器对点进行旋转与位移，

eg.①继续使用【1、什么是解算器】的案例，
②代码节点move内代码修改为，

@P.y += 0.01;

matrix mat = ident();
rotate(mat, radians(3), set(0, 1, 0));
@P *= mat;

③结果：点旋转向上位移，也可以加个“Trail”节点，看看运动轨迹。

3、Basci Growth

例子很简单，随时间变长的螺旋线。简单介绍与组Group节点的结合使用。

eg.①按下图添加节点，及进行设置，及写入代码，

②解算器内的PointWrangle节点代码为，

int npt = addpoint(0, @P);  //当前点位置创建点
addvertex(0, 0, npt);       //将点添加到折线

@P.y += 0.05;               //点位移

matrix mat = ident();
rotate(mat, radians(10), set(0, 1, 0));     //点旋转
@P *= mat;

③结果：点击播放按钮，随时间推移，一条逐渐变成的螺旋线，大概是像下面这个样子(横排版)，

4、对象上的矢量流动

本次做一个基于物体表面的矢量流动。大概像下面这个样子，

 理论：
①把垂直的法线旋转，使法线与模型表面对齐，（下图可结合后面的代码进行理解），

②把对齐与表面的法线复制到【由模型生成的Scatter(点)】，
③在解算器里面对Scatter(点)进行移动等操作，
④设置颜色及对Scatter(点)生成线，方便观察。
操作：
①完整节点及设置如下，完整代码稍后奉上，

②Solver解算器内节点及设置如下，

③完整代码如下，

//filed节点
vector pos = @P * chf('scale');

//根据猪头上的点
vector dir = curlnoise2d(pos + @Time * chf('time'));    //生成的矢量都位于X-Y平面上  
matrix3 mat = dihedral(set(0,0,1), @N);                 //Z轴到法线的旋转矩阵
dir *= mat;                                            //位于X-Y平面上的矢量进行旋转

v@N = dir;                                              //旋转后，法线与猪头表面对齐

//rand_life节点
//给点设置一个随机值，用作生命周期
i@life = floor(rand(@P + chf('seed')) * chi('maxlife'));

//move节点
@P += @N * chf('speed');    //法线方向作为移动方向
i@life--;

//点生命值为0时，移除点，同时又随机生成点
if(i@life < 0){
    vector ruv = rand(@P);
    vector pos = uvsample(1, 'P', 'uv', ruv);
    int pt = addpoint(0, pos);
    int life = floor(rand(@P + chf('seed')) * chi('maxlife'));
    setpointattrib(0, 'life', pt, life);

    removepoint(0, @ptnum);
}

//ncount节点
//当前点附近一定距离内的点，对其上色，即按密度区分上色
int npts[] = nearpoints(0, @P, chf('dist'));

i@count = len(npts);

//flow_line节点
int pt = addpoint(0, @P - @N * chf('len'));
int line = addprim(0, 'polyline', @ptnum, pt);
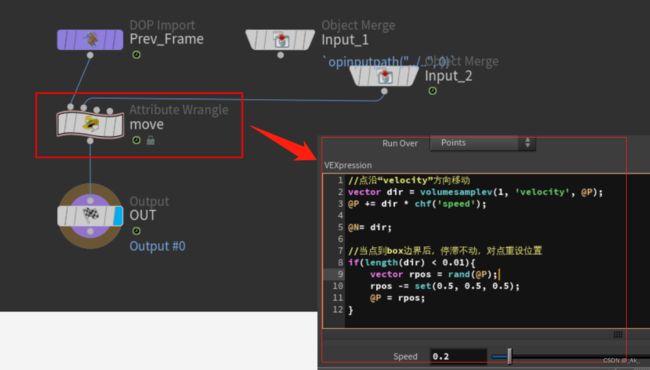
setpointattrib(0, 'Cd', pt, v@Cd);

5、体积上的矢量流动

本次案例跟上一节差不多，只不过对象是Volume。结果大概如下，

eg.①完整节点及设置如下，完整代码稍后奉上，

② Solver解算器内节点及设置如下，

③完整代码如下， 

//volume_flow节点，对体素设置随机向量
vector4 pos = @P * chf('size');
pos.w = @Time * chf('speed');
vector dir = curlnoise(pos);

v@velocity = dir;   //v@velocity值是一个噪波值，噪波的邻值之间过渡平滑

//move 节点
//点沿“velocity”方向移动
vector dir = volumesamplev(1, 'velocity', @P);
@P += dir * chf('speed');

@N= dir;
 
//当点到box边界后，停滞不动，对点重设位置
if(length(dir) < 0.01){
    vector rpos = rand(@P);
    rpos -= set(0.5, 0.5, 0.5);
    @P = rpos;
}

6、几何体修改

在小球表面做“雕刻”。打该结果如下，

主要是使用了sample_sphere_uniform(vector)函数 ，
该函数随机生成一个长度0~1的向量。拓展：参数X、Y可控制旋转，Z控制长度（0~1）。

eg.①完整节点及设置如下，

②solver解算器内的PointWrangle节点代码如下， 

float x = (@Time * chf('speed')) % 1.0;     //X值随时间递增，最大值为1
float y = fit(sin(@Time * chf('speed')), -1.0, 1.0, 0.0, 1.0);  //Y值随时间规律变化

vector dir = sample_sphere_uniform(set(x, y , 1.0));    //一个向量值，长度为1，方向根据X、Y值决定

float rad = chf('rad');                 
float dist = distance(@P, dir);         //雕刻的半径/凸起的范围
dist = min(dist, rad);                  //限制凸起的范围
dist = fit(dist, 0.0, rad, 1.0, 0.0);   
//当前点位置与dir值的位置接近(距离值为0时)，映射为1，即凸起；反之映射为0，不凸起/不作变化
//处于区间的值，按比例凸起

@P += @N * dist * chf('move');      //沿法线方向，move值才是真正的“凸”参数

7、Basic Fractal分形基础

老规矩，先上结果，（也可以用递归。最后一节讲讲），

eg.①完整节点及设置如下，

②solver解算器节点内的两个{PointWrangle节点代码为，

// move节点
vector pos = @P + v@vel;        //vel已设置值（0，0.1,0）
int pt = addpoint(0, pos);
int line = addprim(0, 'polyline', @ptnum, pt);


setpointgroup(0, 'last', @ptnum, 0);    //当前点被组last开除
setpointgroup(0, 'last', pt, 1);        //新的点添加到组last
setpointattrib(0, 'vel', pt, v@vel);

// branch节点
if(@Frame % chi('frame') == 0){
    for(int i=-1; i<=1; i+=2){    //每个点分裂为两个点，两个不同方向
        matrix mat = ident();
        rotate(mat, chf('ang') * $PI * i, set(cos(@Time),0,sin(@Time)));
        
        vector vel = v@vel * mat;
        int pt = addpoint(0, @P + vel);
        int line = addprim(0, 'polyline', @ptnum, pt);
        
       setpointgroup(0, 'last', pt, 1);        //新的点添加到组last
       setpointattrib(0, 'vel', pt, vel);
    }
    setpointgroup(0, 'last', @ptnum, 0);    //当前点被组last开除
}

8、链式解算器

这次做一个小球在盒子里面弹来弹去的嵌套案例，

1）半透明的球在box内弹来弹去，检测中心点是否超出边界
2）小球们在半透明的球里面弹来弹去，检测整个小球(点+球半径)是否超出边界

主要用下面的方法判断小球是否在盒子box内：
①利用小球在box面上的投影（点积值>0，在盒子内）；
②或者使用xyzdist()函数（查找从点到曲面几何图形上最近位置的距离）。
（也可以使用minpos()函数判断）
③对碰到边界的点，进行反弹，原理如下，（看不懂这个旋转的，回去看四元数及矩阵部分），

//使用四元数旋转
velocity *= -1;
vector4 quat = quaternion($PI,@N);
qrotate(quat,velocity);

//使用矩阵旋转
velocity *= -1;
matrix mat = ident();
roatate(mat,$PI,@N);
velocity *= mat;

//与水平面碰撞，仅需将速度的Y值取反值即可
velocity.y *= -1.0;

eg.①总体节点如下，设置并无特别需要注意的地方，

②两个解算节点内节点如下 ，

③各节点完整代码如下，（ primuv函数不理解可以看最后的解释），

//int_vel节点，生成一个随机位置的点

vector vel = rand(chf('seed'));         //值介于0~1之间
vel -= set(0.5, 0.5, 0.5);              //让点集中在中心点附近      
v@N = normalize(vel) * chf('speed');    //vel值作为法线方向

//refelct1节点，单个点在box内反弹，利用点积判断其是否在box内

@P += @N;

int prim;
vector uv;
float dist = xyzdist(1, @P, prim, uv);  //【当前点】距离box的最近面及最近点的uv坐标
vector norm = primuv(1, 'N', prim, uv); //最近面的法线
vector pos = primuv(1, 'P', prim, uv);  //最近点的位置

vector dir = normalize(pos - @P);       //box面上最近点位置 到 点位置 的差值为方向

//根据方向dir值在最近面的投影判断（点积），点是否在box内
//接触到box的面，改变点的运动方向(N)，让它继续在box内继续弹来弹去
if(dot(dir, norm) < 0){
    v@N = -v@N;                 //点/小球法线取反值
    matrix mat = ident();
    rotate(mat, $PI, norm);     //旋转矩阵  面的法线N做旋转轴，旋转180°
    v@N *= mat;                 //点的负法线方向旋转180°
    
    @P = pos + v@N;
}

//int_points，对这些点们生成随机运动方向+自定义运动速度值
vector vel = rand(@P + chf('seed'));
vel -= set(0.5, 0.5, 0.5);

v@N = normalize(vel) * chf('speed');
f@pscale = chf('rad');      //自定义小球半径

f@col = rand(@P) * 1000;

//refelct节点，球与球之间的碰撞反弹
@P += @N;       //小球沿法线移动

//距离当前点位置最近的两个点，索搜索距离为小球直径，第一个最近点为当前小球
int npts[] = nearpoints(0, @P, f@pscale * 2.0, 2);  

if(len(npts) == 2){     //两球发生接触，反弹回去
    int npt = npts[1];
    vector npos = point(0, 'P', npt);   
    
    //不懂可以结合前面的原理图去理解
    vector dir = normalize(npos - @P);
    matrix mat = ident();
    rotate(mat, $PI, dir);
    v@N = -v@N * mat;       //这个法线为反弹后的方向/向量
    
    @P = npos - dir * f@pscale * 2.0 + v@N;     //小球位置更新
    
    f@col = rand(@P + chf('seed')) * 1000;      //碰后换色
}

//move节点，与上面的代码类似，这次是判断运动的小球(+半径)是否在box内
@P += @N;

int prim;
vector uv;
float dist = xyzdist(1, @P, prim, uv);  //【当前点】距离box的最近面及最近点的uv坐标
vector norm = primuv(1, 'N', prim, uv); //最近面的法线
vector pos = primuv(1, 'P', prim, uv);  //最近点的位置


vector ppos = @P + normalize(pos-@P) * f@pscale;    //引入半径
vector dir = normalize(pos - ppos);       //box面上最近点位置 到 点位置 的差值为方向

//根据方向dir值在最近面的投影判断（点积），点是否在box内
if(dot(dir, norm) < 0){
    v@N = -v@N;                 //点/小球法线取反值
    matrix mat = ident();
    rotate(mat, $PI, norm);     //旋转矩阵  面的法线N做旋转轴，旋转180°
    v@N *= mat;                 //点的负法线方向旋转180°
    
    @P = pos + dir * f@pscale + v@N;
}

//Alpha节点，对大球设置透明度
f@Alpha = 0.2;

④结果：
颜色color 节点记得选择col属性，其它自定义参数看着调。

9、拓展—primuv函数、xyzdist函数

primuv 是根据给出的uv 坐标 和 面序号,读取任意属性,和这个函数类似的是uvsample()函数.
详细可以看这篇文章知乎@刘鹏云。