算法与数据结构（五）--二叉树入门

符号表的增删查操作，随着元素个数N的增多，其耗时也是线性增多的，时间复杂度都是O(n)，为了提高运算效率，我们学习树这种数据结构。

目录

一.树的基本定义

二.树的相关术语

三.二叉树的基本定义

四.二叉树的链表实现

1.二叉树结点类：

结点类API设计:​编辑

代码实现：

2.二叉树API设计：​编辑

3.二叉树实现思想

五.二叉树的基础遍历

前序遍历

中序遍历

后序遍历

六.二叉树的层序遍历

七.二叉树的最大深度问题

总结

---

一.树的基本定义

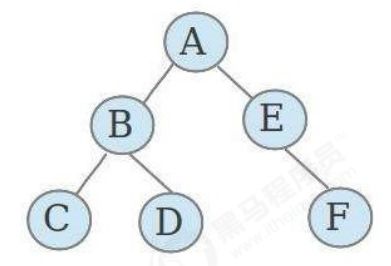
树是由n（n>=1）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一颗倒挂的树，也就是说它是根朝上，而叶朝下的。

 树具有以下特点：
1.每个结点有零个或多个子结点；
2.没有父结点的结点为根节点；
3.每一个非根结点只有一个父结点；
4.每个结点及其后代结点整体上可以看做是一棵树，成为当前结点的父结点的一个子树；

二.树的相关术语

结点的度：
一个结点含有的子树的个数称为该结点的度
叶结点：
度为0的结点称为叶结点，也可以叫做终端结点；
分支结点：
度不为0的结点称为分支结点，也可以叫做非终端结点
结点的层次：
从根结点开始，根结点的层次为1，根的直接后继层次为2，以此类推
结点的层序编号：
从树中的结点，按照从上层到下层，同层从左到右的次序排成一个线性序列，把他们编成连续的自然数。
树的度：
树中所有结点的度的最大值
树的高度(深度)：
树中结点的最大层次
森林：
m（m>=0）个互不相交的树的集合，将一个非空树的根结点删去，树就变成了一个森林；给森林增加一个统一的根结点，森林就变成了一棵树。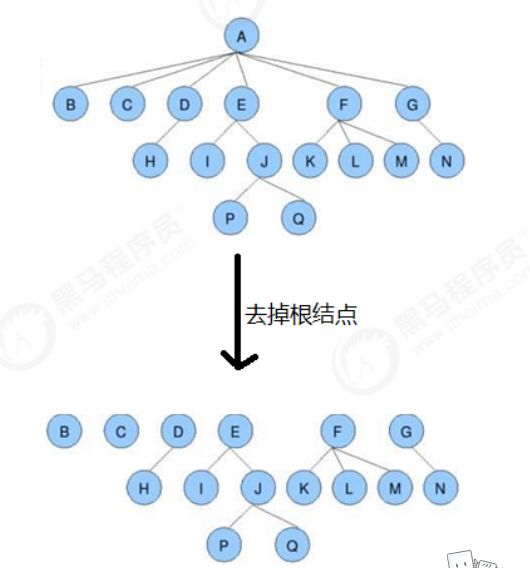

孩子结点：
一个结点的直接后继结点称为该结点的孩子结点
双亲结点（父节点）：
一个结点的直接前驱称为该结点的双亲结点
兄弟结点：
同一双亲结点的孩子结点间互称兄弟结点

三.二叉树的基本定义

二叉树就是度不超过2的树（每个结点最多有两个子结点）

满二叉树：
一个二叉树，如果每一个层的结点树都达到最大值，则这个二叉树就是满二叉树。

完全二叉树：
叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在盖层最左边的若干位置的二叉树。

四.二叉树的链表实现

1.二叉树结点类：

按照面向对象的思想，我们设计一个结点类来描述结点这个事物。

结点类API设计:

代码实现：

public class Node {
    //存储键
    public Key key;
    //存储值
    public Value vaule;
    //记录左子结点
    public Node left;
    //记录右子结点
    public Node right;
    public Node(Key key, Value value, Node left, Node right){
        this.key=key;
        this.vaule=value;
        this.left=left;
        this.right=right;
    }
}

2.二叉树API设计：

其他补充api：
private Node min(Node x)        找出指定树x中，最小键所在的结点
private Node max(Node x)        找出指定树x中，最大键所在的结点

3.二叉树实现思想

插入方法put实现思想：
1.如果当前树中没有任何一个结点，则直接把新结点当做根结点使用
2.如果当前树不为空，则从根结点开始：
2.1 如果新结点的key小于当前结点的key，则继续找当前结点的左子结点
2.2 如果新结点的key大于当前结点的key，则继续找当前结点的右子结点
2.3 如果新结点等于当前结点的key，则树中已经存在这样的结点，替换该结点的value值即可。

查询方法get实现思想：

从根节点开始：
1.如果要查询的key小于当前结点的key，则继续找当前结点的左子结点；
2.如果要查询的key大于当前结点的key，则继续找当前结点的右子结点；
3.如果要查询的key等于当前结点的key，则树中返回当前结点的value。

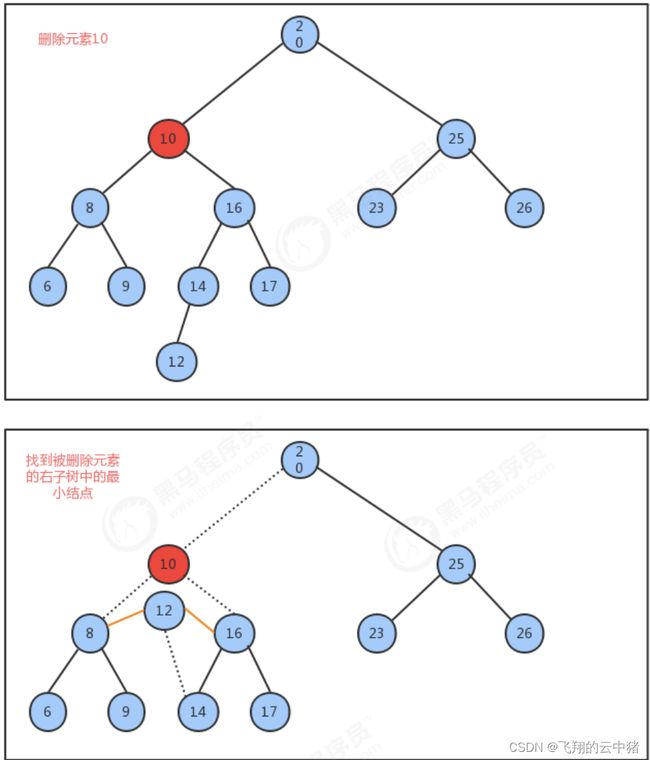
删除方法delete实现思想：

1.找到被删除结点
2.找到被删除结点右子树中的最小结点minNode
3.删除右子树中的最小结点
4.让被删除结点的左子树称为最小结点minNode的左子树，让被删除结点的右子树称为最小结点minNode的右子树
5.让被删除结点的父节点指向最小结点minNode

 

五.二叉树的基础遍历

树的结构和线性表结构不一样，没有办法从头开始依次向后遍历，所以存在按照什么样的搜索路径进行遍历的问题。

我们可以把二叉树的遍历分为以下三种（简单说就是按什么时候访问根节点进而分为前中后）：
1.前序遍历：先访问根节点，然后访问左子树，最后访问右子树。
2.中序遍历：先访问左子树，中间访问根节点，最后访问右子树。
3.后序遍历：先访问左子树，再访问右子数，最后访问根节点。

可以看到其实就是三种操作变换顺序罢了。

前序遍历

实现步骤：
1.把当前结点的key放入到队列中；
2.找到当前结点的左子树，如果不为空，递归遍历左子树；
3.找到当前结点的右子树，如果不为空，递归遍历右子树。

相关题目链接：

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

中序遍历

实现步骤：
1.找到当前结点的左子树，如果不为空，递归遍历左子树；
2.把当前结点的key放入到队列中；
3.找到当前结点的右子树，如果不为空，递归遍历右子树。

相关题目链接：

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

后序遍历

实现步骤：
1.找到当前结点的左子树，如果不为空，递归遍历左子树；
2.把当前结点的key放入到队列中；
3.找到当前结点的右子树，如果不为空，递归遍历右子树。

相关题目链接：
力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

六.二叉树的层序遍历

所谓层序遍历，就是从根节点（第一层开始），依次向下，获取每一层所有节点的值，
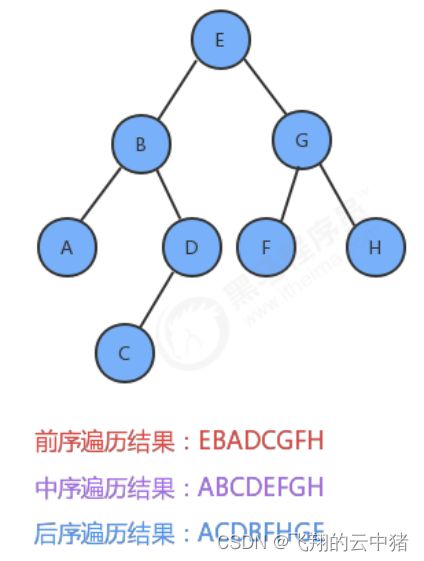
有二叉树如下：

那么层序遍历的结果是：EBGADFHC。

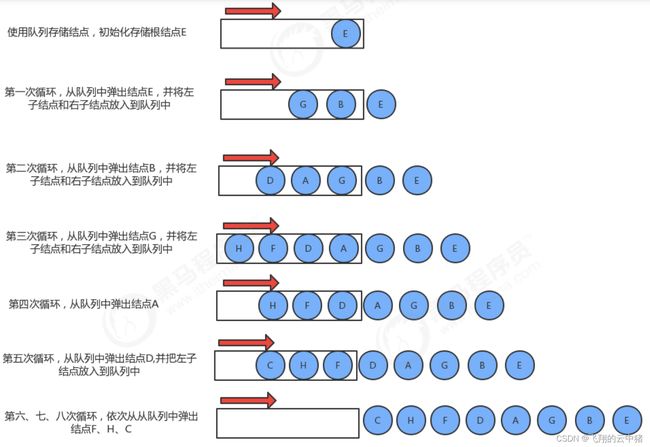
实现步骤：
1.创建队列，存储每一层的结点；
2.使用循环从队列中弹出一个结点；
2.1获取当前结点的key；
2.2如果当前结点的左子结点不为空，则把左子结点放入到队列中；
2.3如果当前结点的右子结点不为空，则把右子结点放入到队列中。

题目链接：
力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

七.二叉树的最大深度问题

需求：给定一颗树，计算树的最大深度（树的根节点到最远叶子结点的最长路径上的结点数）。

实现步骤：
1.如果根结点为空，则最大深度为0；
2.计算左子树的最大深度；
3.计算右子树的最大深度；
4.当前树的最大深度=左子树的最大深度和右子树的最大深度中的较大者+1

题目链接：
力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

总结

可以看到关于树的很多操作都要用到递归。