利用matlab实现一维搜索算法

         通过五种方法实现全局极小值点的求解。其中，“成功-失败法”是试探法；区间收缩法，包括二分法、0.618法；函数逼近法，包括Newton法、二次插值法。

1.“成功-失败”法，又称进退法

function [k,interval] = forward_back(fx,x0,h0,t)
% 输入目标函数fx、初始点x0、初始步长h0和加倍系数t
% 退出条件：当k不等于1且f(x1) >= f(x0)时，程序结束
% 采用"进退法"确定并输出得到的最小搜索区间[m,n]

f = inline(fx);        % 将 fx字符串 转换为 函数f(x)
k = 0;                 % 迭代次数（如果第1次目标函数就没有下降，将作为反向搜索)
a = x0;                % 初始化最值区间的左端点
h = h0;                % 初始化迭代的步长

while true              
    x1 = x0 + h; 
    k = k + 1;
    if f(x1) < f(x0)   % 判断搜索方向，保证是下降方向
        h = t * h;      % 加大步长，一般情况下选择加倍系数t = 2
        a = x0;         % 更新最值区间的左端
        x0 = x1;        % 更新初始点
    elseif f(x1) >= f(x0)
       if k == 1        % 判断初始方向是否错误
          h = -h;       % 方向错误，选择反方向
          x0 = x1;      % 更新初始点
       else                
           break;
       end
    end
end

 m = min(a,x1);
 n = max(a,x1);
interval = sprintf('[%.4f,%.4f]',m,n);  % 格式化输出区间
end

  

注意：关于变量没有定义的问题：要在MATLAB中将函数存入.m文件再在命令窗口调用（文件与函数同名）；调用函数前，在命令行窗口定义变量syms x，即如下图：

2.黄金分割法，又称0.618法

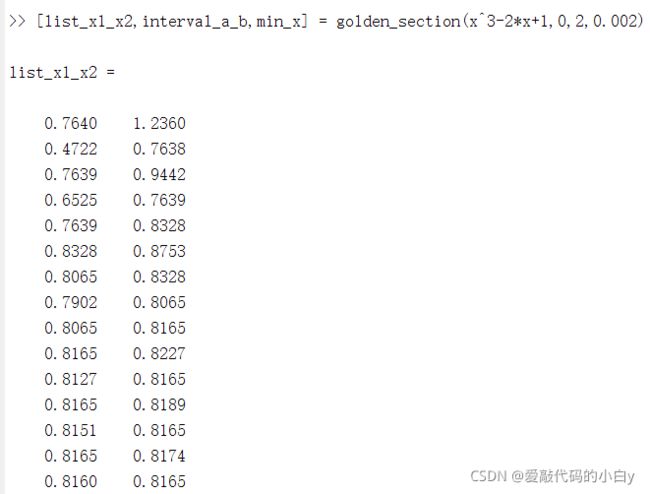
function [list_x1_x2,interval_a_b,min_x] = golden_section(fx,a,b,accuracy)
% 输入目标函数fx、初始区间的端点a、b和精确度accuracy
% 0.618法则，又称黄金分割法，是一种区间缩减的方法
% 缩减区间的原则：去坏留好
% 迭代时，遵循对称原则 (x1-a=b-x2) ，并保持缩减比t不变
% 当最终区间长度b-a小于或者等于accuracy时，迭代退出

format short             % 输出为小数

t = 0.618;               % 缩减比
x1 = a + (1-t)*(b-a);    
x2 = a + t*(b-a);  
f = inline(fx);          % 将 fx字符串 转换为 函数法f(x)

list_x1 = []; 
list_x2 = []; 
list_x1_x2 = []; 
interval_a = [];
interval_b = [];
interval_a_b = [];

while (b-a) > accuracy
    list_x1(end+1) = x1;                         % 每次迭代中使用的x1
    list_x2(end+1) = x2;                         % 每次迭代中使用的x2

    if f(x1) > f(x2)
        a = x1;
        x1 = a + (1-t)*(b-a);    
        x2 = a + t*(b-a);  
    else
        b = x2;
        x1 = a + (1-t)*(b-a);    
        x2 = a + t*(b-a);    
    end
    interval_a(end+1) = a;
    interval_b(end+1) = b;
end

min_x = (a+b)/2;
list_x1_x2 = [list_x1;list_x2]';
interval_a_b = [interval_a;interval_b]';
end

 

3.二分法

function [list_min_x,interval_a_b,min_x] = half_section(fx,a,b,accuracy)

% 输入目标函数fx、初始区间的端点a、b和精确度accuracy
% 二分法求极小值
% 如果f'(a)*f'(b)<0，则定义域内一定存在min_x，使得f'(min_x)=0
% 当最终区间长度b-a小于或者等于accuracy时，迭代退出


format rat                   % 将小数化为分数
syms x dy                    % syms的作用是定义符号变量

list_min_x = [];
interval_a = [];
interval_b = [];
interval_a_b = [];
dy = inline(diff(fx,x));      % inline为内联函数;diff求一阶导数

while (b-a) > accuracy
    if ((dy(a)*dy(b)) < 0)
        x0 = (a+b)/2;
        list_min_x(end+1) = x0;
        
        if (dy(a)*dy(x0)) < 0
            b = x0;
        elseif (dy(x0)*dy(b)) < 0
            a = x0;
        end
        interval_a(end+1) = a;
        interval_b(end+1) = b;
    else
        disp("请改变区间的端点");
        break;
    end
end

list_min_x = list_min_x';
interval_a_b = [interval_a;interval_b]';
min_x = list_min_x(length(list_min_x));
end

>> [list_min_x,interval_a_b,min_x] = half_section(x^3-2*x+1,0,2,0.004)

list_min_x =

       1       
       1/2     
       3/4     
       7/8     
      13/16    
      27/32    
      53/64    
     105/128   
     209/256   

interval_a_b =

       0              1       
       1/2            1       
       3/4            1       
       3/4            7/8     
      13/16           7/8     
      13/16          27/32    
      13/16          53/64    
      13/16         105/128   
     209/256        105/128   

min_x =

     209/256   

4.Newton法

function [list_x,min_x] = Newton(fx,x1,error)
syms x dy ddy
format short

f = inline(fx);               % 将 fx字符串 转换为 函数法f(x)
dy = inline(diff(fx,x));      % inline为内联函数;diff求一阶导数
ddy = inline(diff(diff(fx,x),x));
list_x = [];

while not (dy(x1)

 [min_x,list_x,ddy] = Newton(x^4-4*x^3-6*x^2-16*x+4, 6,0.01)

min_x =

    4.0105

list_x =

    6.0000    4.7536    4.1645    4.0105
 

5.二次插值法

function [min_x,list_min_x] = Quadratic_Interpolation(fx,x0,h,t,error)

format short
syms x

f = inline(fx);
list_min_x = [];

% 用成功-失败法，即forward_back，得到“高-低-高”三点
[~,list_x0,~,m,n] = forward_back(fx, x0, h, t);
x1 = m;
x2 = list_x0(length(list_x0));
x3 = n;

% 用二次插值法逼近极小点
x = [x1,x2,x3];
y = [f(x1),f(x2),f(x3)];
p = polyfit(x,y,2);    % 多项式拟合函数，返回降幂排列的多项式系数
min_x = -p(2)/(2*p(1));
list_min_x(end+1) = min_x;
while not (abs(min_x-x2)

 [min_x,list_min_x] = Quadratic_Interpolation(3*x^3-4*x+2,-1/2,1/2,2,0.2)

min_x =

    0.6081

list_min_x =

    0.5417    0.6081

---