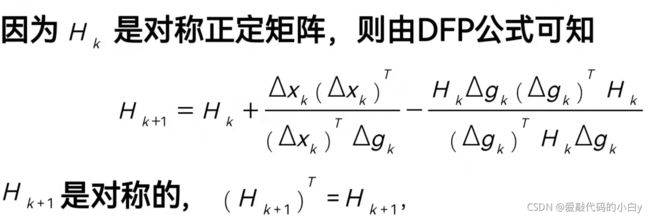利用matlab实现无约束最优化方法
目录
1.最速下降法
2.加速梯度法——最速梯度下降法的改进
3.Newton法-----多维
4.阻尼Newton法
5、FR共轭梯度法
6、变尺度法---DFP算法
1.最速下降法
最速下降法-----两个特征:1.相邻两次迭代的搜索方向正交,即在向极小值点逼近的过程中会出现锯齿现象,从而导致逼近速度越来越慢;2.给定二元正定二次函数,用最速梯度下降法求其极小值点,会产生点列Xi(i = 1,2...):其中偶数点列X2k (i = 1,2...)和奇数点列X2k+1 (i = 1,2...)分别落在两条相交的直线上,且交于极小值点。
在用于正定的二次函数求极小值点时,存在两种情况:1.目标函数的等值线为圆时,不存在锯齿现象,且只需一步就可以迭代到极小值点;2.目标函数的等值线是椭圆时,存在锯齿现象,且椭圆越扁,锯齿现象越明显。
function [n,list_t,list_x1,list_x2] = fastest_gradient_descent(fx,x10,x20,error)
% 最小梯度下降算法求二元函数的的全局极小值点
% t代表步长,t_value代表最佳步长;x1、x2代表变量;n代表迭代次数
syms x1 x2 t
format short
g = [diff(fx,x1),diff(fx,x2)]; % 求梯度
v = [x1,x2];
v0 = [x10,x20];
g0 = subs(g,v,v0); % 求初始点[x0,y0]的梯度值; subs: Symbolic substitution
n = 0; % 迭代次数
list_t = [];
list_x1 = [];
list_x2 = [];
temp = norm(g0);
while not (temp < error)
% 将每一次迭代的变量,分别保存到list_x1.list_x2
list_x1(end+1) = v0(1);
list_x2(end+1) = v0(2);
% 最速下降方向
d = - g0;
% 利用精确一维搜索得到最佳步长
ft = subs(fx,v,v0 + t * d);
dft = diff(ft,t);
t_value = double(solve(dft));
list_t(end+1) = t_value; % 记录最佳步长
% 更新并进行准备下一次迭代
v0 = v0 + t_value * d; % 求下一个迭代点
g0 = subs(g,v,v0); % 下一个迭代点的梯度
temp = norm(g0); % 向量范数和矩阵范数
% 记录迭代次数
n = n + 1;
end
end结论:二元二次函数f(x1,x2) = x1^2+2*x2^2-2*x1*x2-4*x1,从(1,1)点出发迭代17次,得到局部极小值点(3.9883,1.9961)
>> [n,list_t,list_x1,list_x2] = fastest_gradient_descent(x1^2+2*x2^2-2*x1*x2-4*x1,1,1,0.01)
n =
17
list_t =
1 至 11 列
0.2500 0.5000 0.2500 0.5000 0.2500 0.5000 0.2500 0.5000 0.2500 0.5000 0.2500
12 至 17 列
0.5000 0.2500 0.5000 0.2500 0.5000 0.2500
list_x1 =
1 至 11 列
1.0000 2.0000 2.5000 3.0000 3.2500 3.5000 3.6250 3.7500 3.8125 3.8750 3.9063
12 至 17 列
3.9375 3.9531 3.9688 3.9766 3.9844 3.9883
list_x2 =
1 至 11 列
1.0000 0.5000 1.5000 1.2500 1.7500 1.6250 1.8750 1.8125 1.9375 1.9063 1.9688
12 至 17 列
1.9531 1.9844 1.9766 1.9922 1.9883 1.9961
2.加速梯度法——最速梯度下降法的改进
function [n,list_t,list_x1,list_x2] = fastest_gradient_descent_update(fx,x10,x20,error)
% 加速梯度下降算法求二元函数的的全局极小值点
% t代表步长;x1、x2代表变量;n代表迭代次数
syms x1 x2 t
format short
g = [diff(fx,x1),diff(fx,x2)]; % 求梯度
v = [x1,x2];
v0 = [x10,x20];
g0 = subs(g,v,v0); % 求初始点[x0,y0]的梯度值; subs: Symbolic substitution
k = 0;
n = 0; % 迭代次数
list_t = [];
list_x1 = [];
list_x2 = [];
% 将每一次迭代的变量,分别保存到list_x1.list_x2
list_x1(end+1) = v0(1);
list_x2(end+1) = v0(2);
temp = norm(g0);
while not (temp < error)
if k == 2
% 下降方向
l_1 = length(list_x1);
l_2 = length(list_x2);
x1 = [list_x1(l_1 - 2),list_x2(l_2 - 2)];
x2 = [list_x1(l_1),list_x2(l_2)];
d = x2 - x1;
k = 0;
else
% 最速下降方向
d = - g0;
k = k + 1;
end
% 利用精确一维搜索得到最佳步长
ft = subs(fx,v,v0 + t * d);
dft = diff(ft,t);
t_value = double(solve(dft));
list_t(end+1) = t_value; % 记录最佳步长
% 更新并进行准备下一次迭代
v0 = v0 + t_value * d; % 求下一个迭代点
g0 = subs(g,v,v0); % 下一个迭代点的梯度
temp = norm(g0); % 向量范数和矩阵范数
% 将每一次迭代的变量,分别保存到list_x1.list_x2
list_x1(end+1) = v0(1);
list_x2(end+1) = v0(2);
% 记录迭代次数
n = n + 1;
end
end结论:二元二次函数f(x1,x2) = x1^2+2*x2^2-2*x1*x2-4*x1,从(1,1)点出发迭代3次,得到局部极小值点(4,2)
[n,list_t,list_x1,list_x2] = fastest_gradient_descent_update(x1^2+2*x2^2-2*x1*x2-4*x1,1,1,0.01)
n =
3
list_t =
0.2500 0.5000 1.0000
list_x1 =
1.0000 2.0000 2.5000 4.0000
list_x2 =
1.0000 0.5000 1.5000 2.0000
3.Newton法-----多维
利用Newton法求n元正定二次函数的极小值点,从任意初始点出发,一步迭代即可到达极小值点。
function [n,list_x1,list_x2] = Newton_two_dimension(fx,x10,x20,eps)
% 最小梯度下降算法求二元函数的的全局极小值点
% 固定步长t=1;x1、x2代表变量;n代表迭代次数
syms x1 x2 d
format short
g = [diff(fx,x1),diff(fx,x2)]; % 求梯度
Hessian = hessian(fx,[x1,x2]); % 求hessian矩阵
v = [x1,x2];
v0 = [x10,x20];
g0 = subs(g,v,v0); % 求初始点[x0,y0]的梯度值; subs: Symbolic substitution
n = 0; % 迭代次数
list_x1 = [];
list_x2 = [];
t = 1;
% 将每一次迭代的变量,分别保存到list_x1.list_x2
list_x1(end+1) = v0(1);
list_x2(end+1) = v0(2);
temp = norm(g0);
while not (temp < eps)
eigValue = eig(subs(Hessian,v,v0));
if all(eigValue) > 0
% 下降方向
d = - inv(subs(Hessian,v,v0)) * subs(g,v,v0)';
% 更新
v0 = v0 + t * d';
% 将每一次迭代的变量,分别保存到list_x1.list_x2
list_x1(end+1) = v0(1);
list_x2(end+1) = v0(2);
% 准备下一次迭代
g0 = subs(g,v,v0);
temp = norm(g0);
n = n + 1;
else
disp("Hessian矩阵不是正定矩阵");
end
end
end结论:二元二次函数f(x1,x2) = x1^2+2*x2^2-2*x1*x2-4*x1,从(1,1)点出发迭代1次,得到局部极小值点(4,2)
>> [n,list_x1,list_x2] = Newton_two_dimension(x1^2+2*x2^2-2*x1*x2-4*x1,1,1,0.01)
n =
1
list_x1 =
1 4
list_x2 =
1 2
4.阻尼Newton法
利用阻尼Newton法求n元正定二次函数的极小点,从任意初始点出发,一步迭代即可到达极小点。
function [n,list_x1,list_x2] = damping_newton_method(fx,x10,x20,error)
% 最小梯度下降算法求二元函数的的全局极小值点
% 步长t;x1、x2代表变量;n代表迭代次数
syms x1 x2 d t
format short
g = [diff(fx,x1),diff(fx,x2)]; % 求梯度
Hessian = hessian(fx,[x1,x2]); % 求hessian矩阵
v = [x1,x2];
v0 = [x10,x20];
g0 = subs(g,v,v0); % 求初始点[x0,y0]的梯度值; subs: Symbolic substitution
n = 0; % 迭代次数
list_x1 = [];
list_x2 = [];
list_t = [];
% 将每一次迭代的变量,分别保存到list_x1.list_x2
list_x1(end+1) = v0(1);
list_x2(end+1) = v0(2);
temp = norm(g0);
while not (temp < error)
eigValue = eig(subs(Hessian,v,v0));
if all(eigValue) > 0
list_dft = [];
% 下降方向
d = - double(inv(subs(Hessian,v,v0)) * subs(g,v,v0)');
% 利用精确一维搜索得到最佳步长
ft = subs(fx,v,v0 + t * d'); % f=@(x)是通过匿名函数的方法定义函数,inline( )是通过内联函数的方法定义函数
dft = diff(ft,t);
t_value = double(solve(dft));
i = 1;
dft = inline(diff(ft,t));
while i <= length(t_value)
list_dft(end+1) = abs(dft(t_value(i))); % abs(z):求复数z的值
i = i + 1;
end
[~,index_min] = min(list_dft);
t_value = t_value(index_min);
list_t(end+1) = t_value; % 记录最佳步长
% 更新
v0 = v0 + t_value * d';
% 将每一次迭代的变量,分别保存到list_x1.list_x2
list_x1(end+1) = v0(1);
list_x2(end+1) = v0(2);
% 准备下一次迭代
g0 = subs(g,v,v0);
temp = norm(g0);
n = n + 1;
else
disp("Hessian矩阵不是正定矩阵");
end
end
end
>> [n,list_x1,list_x2] = damping_newton_method(x1+x2^2+x1^4+2*x1^2*x2^2+8*x1^2*x2^6,1,1,0.1)
n =
4
list_x1 =
1.0000 1.3043 -0.6241 -0.6597 -0.6300
list_x2 =
1.0000 0.5032 0.2403 0.0060 -0.0000
5、FR共轭梯度法
function [fv, bestx, iter_num] = FR_conjungate_gradient_method(f, x, x0, eps, show_detail)
%% conjungate gradient method
% Input:
% f - syms function
% x - row cell arrow for input syms variables
% x0 - init point
% eps - tolerance
% show_detail - a bool value for whether to print details
% Output:
% fv - minimum f value
% bestx - mimimum point
% iter_num - iteration count
%%
% 1、单元数组(cell array)
% 其中的每个元素为(cell) cell可以包含任何类型的matlab数据
% 一个单元数组中可以包含不同的cell
% (1)创建cell数组
% 利用cell函数,如:cell(2,3)生成一个2*3的cell数组。或者直接等于一个元组,如:c={[1 2 3 4]}
% (2)访问单元数组:两种方法:使用括号、使用花括号
% 使用括号得到的是那个单元(cell)。使用花括号得到的是那个单元的具体内容
% 如:b=cell(1); b{1}=[1 2 3 4]。当显示b(1)时得到[1x4 double]。而使用b{1}得到1 2 3 4
% (3)赋值:有了前面访问的方法即可明白,要赋值也有两种方法:
% 使用括号时,须将一个cell赋给左边;使用花括号时可以直接将值赋给左边
%% init
% show initial info
if show_detail
fprintf('Initial:\n');
fprintf('f = %s, x0 = %s, epsilon = %f\n\n', char(f), num2str(x0), eps);
end
syms lambdas
% n is the dimension of cell x
n = length(x);
% compute differential of function f stored in cell nf
df = cell(1, n);
for i = 1 : n
df{i} = diff(f, x{i});
% disp(nf{i});
end
dfv = subs(df, x, x0);
dfv_pre = dfv;
% init count, k and xv for x value.
count = 0; % 迭代次数
k = 0; % 记录迭代次数当k==n,重新赋初值开始
xv = x0;
% initial search direction
d = - dfv;
%% loop
while (norm(dfv) > eps)
%% one-dimensional search % 得到最佳步长
xv = xv + lambdas * d;
flambda = subs(f, x, xv);
dflambda = diff(flambda);
lambda = solve(dflambda);
% get rid of complex and minus solution
if length(lambda) > 1
i = 1;
list_dflambda = [];
dflambda = inline(diff(flambda,lambdas));
while i <= length(lambda)
list_dflambda(end+1) = abs(dflambda(lambda(i))); % abs(z):求复数z的值
i = i + 1;
end
[~,index_min] = min(list_dflambda);
lambda = lambda(index_min);
end
% lambda is too small, stop iteration
if lambda < 1e-5
break;
end
%% update
% convert sym to double
xv = double(subs(xv, lambdas, lambda));
% compute the differential
dfv = subs(df, x, xv);
% compute alpha based on FR formula
alpha = sumsqr(dfv) / sumsqr(dfv_pre);
% update conjungate direction
d = -dfv + alpha * d;
% save the previous dfv
dfv_pre = dfv;
% update counters
count = count + 1;
k = k + 1;
% show iteration info
if show_detail
fprintf('Iteration: %d\n', count);
fprintf('x(%d) = %s, 精确一维搜索的步长lambda = %f\n', count, num2str(xv), lambda);
fprintf('梯度df(x) = %s, 梯度的模norm(df) = %f\n', num2str(double(dfv)), norm(double(dfv)));
% alpha:本次迭代方向受上次迭代方向影响的加权系数
fprintf('迭代的下降方向d = %s, 加权系数alpha = %f\n', num2str(double(d)), double(alpha));
fprintf('\n');
end
% if k >= n ,reset the conjungate direction
if k >= n
k = 0;
d = - dfv; % 迭代次数超过n次时,第n+1个xv作为初值,梯度方向从第n+1次的梯度方向开始,重新迭代
end
end
%% output
fv = double(subs(f, x, xv));
bestx = double(xv);
iter_num = count;
end>> [fv, bestx, iter_num] = FR_conjungate_gradient_method(x1^2+2*x2^2-4*x1-2*x1*x2, {x1,x2}, [1,1], 0.01, true)
Initial:
f = x1^2 - 2*x1*x2 - 4*x1 + 2*x2^2, x0 = 1 1, epsilon = 0.010000
Iteration: 1
x(1) = 2 0.5, 精确一维搜索的步长lambda = 0.250000
梯度df(x) = -1 -2, 梯度的模norm(df) = 2.236068
迭代的下降方向d = 2 1.5, 加权系数alpha = 0.250000
Iteration: 2
x(2) = 4 2, 精确一维搜索的步长lambda = 1.000000
梯度df(x) = 0 0, 梯度的模norm(df) = 0.000000
迭代的下降方向d = 0 0, 加权系数alpha = 0.000000
fv =
-8
bestx =
4 2
iter_num =
2
6、变尺度法---DFP算法
function [fv, bestx, iter_num] = DFP(f, x, x0, eps, show_detail)
%% init
% show initial info
if show_detail
fprintf('Initial:\n');
fprintf('f = %s, x0 = %s, epsilon = %f\n\n', char(f), num2str(x0), eps);
end
syms lambdas
% n is the dimension of cell x
n = length(x);
% compute differential of function f stored in cell nf
df = cell(1, n);
for i = 1 : n
df{i} = diff(f, x{i});
% disp(nf{i});
end
dfv = subs(df, x, x0);
dfv_pre = dfv;
% init count, k and xv for x value.
count = 0; % 迭代次数
k = 0; % 记录迭代次数当k==n,重新赋初值开始
xv = x0;
xv_pre = xv;
% initial search direction
Hk = eye(2);
Hk_pre = eye(2);
p = - Hk * dfv'; % 初始方向
%% loop
while (norm(dfv) > eps)
%% one-dimensional search % 得到最佳步长
xv = xv + lambdas * p';
flambda = subs(f, x, xv);
dflambda = diff(flambda);
lambda = solve(dflambda);
% get rid of complex and minus solution
if length(lambda) > 1
i = 1;
list_dflambda = [];
dflambda = inline(diff(flambda,lambdas));
while i <= length(lambda)
list_dflambda(end+1) = abs(dflambda(lambda(i))); % abs(z):求复数z的值
i = i + 1;
end
[~,index_min] = min(list_dflambda);
lambda = lambda(index_min);
end
% lambda is too small, stop iteration
if lambda < 1e-5
break;
end
%% update
% convert sym to double
xv = double(subs(xv, lambdas, lambda));
% compute the differential
dfv = subs(df, x, xv);
% compute H based on FR formula
delta_x = xv - xv_pre;
delta_dfv = dfv - dfv_pre;
Hk = Hk_pre + (delta_x' * delta_x) / (delta_x * delta_dfv') - (Hk_pre * delta_dfv' * delta_dfv * Hk_pre) / (delta_dfv * Hk_pre * delta_dfv');
% update conjungate direction
p = - Hk * dfv';
% save the previous dfv
dfv_pre = dfv;
xv_pre = xv;
Hk_pre = Hk;
% update counters
count = count + 1;
k = k + 1;
%% show iteration info
if show_detail
fprintf('Iteration: %d\n', count);
fprintf('x(%d) = %s, \t精确一维搜索的步长 lambda = %f\n', count, num2str(xv), lambda);
fprintf('梯度 df(x) = %s, \t梯度的模 norm(df(x)) = %f\n', num2str(double(dfv)), norm(double(dfv)));
disp('迭代的下降方向 d = ');
disp(p);
disp('\n尺度矩阵 Hk = ');
disp(double(Hk));
end
%% if k >= n ,reset the conjungate direction
if k >= n
k = 0;
d = - dfv; % 迭代次数超过n次时,第n+1个xv作为初值,梯度方向从第n+1次的梯度方向开始,重新迭代
end
end
%% output
fv = double(subs(f, x, xv));
bestx = double(xv);
iter_num = count;
end
>> [fv, bestx, iter_num] = DFP(2*x1^2+x2^2-4*x1+2, {x1,x2}, [2,1], 0.001, true)
Initial:
f = 2*x1^2 - 4*x1 + x2^2 + 2, x0 = 2 1, epsilon = 0.001000
Iteration: 1
x(1) = 0.88889 0.44444, 精确一维搜索的步长 lambda = 0.277778
梯度 df(x) = -0.44444 0.88889, 梯度的模 norm(df(x)) = 0.993808
迭代的下降方向 d =
4/17
-16/17
\n尺度矩阵 Hk =
0.2810 -0.1242
-0.1242 0.9967
Iteration: 2
x(2) = 1 0, 精确一维搜索的步长 lambda = 0.472222
梯度 df(x) = 0 0, 梯度的模 norm(df(x)) = 0.000000
迭代的下降方向 d =
0
0
\n尺度矩阵 Hk =
0.2500 0
0 0.5000
fv =
0
bestx =
1 0
iter_num =
2