为什么InnoDB索引采用B+树，而不是红黑树或者B树

前言

在Mysql InnoDB引擎中使用的是B+树作为主要的索引数据结构，为什么不使用平衡二叉树或者红黑树呢？

因为数据库是建立在磁盘上面的，而不是像红黑树等平衡树是建立在内存中的。对于磁盘来说，每次子树的查找就是一次随机I/O，树越高，需要的随机I/O的次数就越多，所以宁愿每个节点中的关键字多一点，把它加载到内存中进行二分查找，也不要多两次随机I/O(磁盘随机I/O和内存随机I/O的速度差了10万倍左右)。

在磁盘里对数据的每次随机I/O都需要排队、旋转等待、寻道等操作，耗时大概在10ms左右。而顺序I/O则没有以上这些操作，相对来说就快多了，当顺序读取一行数据是0.01ms时，同样读取10000行数据，如果它们在磁盘上是按读取顺序排列的，则只需要一次随机I/O和10000次顺序IO，即10ms+0.01ms*10000=110ms。如果不是按读取顺序排列的，则需要10000次随机I/O，即10000*10ms=100s。以上大家应该可以看出来两者的差距，所以为了提高性能，Mysql必须减少随机I/O的次数。

在本篇博客中，我们将对比红黑树、B+树和B树之间的区别，以此来分析为什么B+树更适合作为数据库索引数据结构。

红黑树

红黑树是一种平衡二叉树，其中叉代表的是子树指针的数量，和所有二叉树一样，它的叉=2，树高是，所以查找一个关键字的渐近时间复杂度为，它适合作为内存中的一种有序的结构来使用，但是面对磁盘千万级的数据量，它的树高将达到两位数，很不利于磁盘中的操作。

关于二叉树和红黑树的细节请参考我的另一篇博客：HashMap源码分析，Java中的符号表

B+树

B+树也是一种平衡树，但是它的叉是可动态指定的，在Mysql中大约是1170。因为叉的数量足够多，所以在同等数量级下，树高更低()。通过增加单个节点中关键字的数量，来降低树高，这种结构更适合磁盘。

在Mysql中，最小的数据单元是页，一个页默认是16KB，假设数据表的主键是BIGINT类型，指针一般是6B。一个关键字为主键加子树指针的组合，大小是8+6=14B，所以理论上一个内部节点页可以存储的关键字数量为16KB/14B=1170个。

B+树的定义如下：

• 节点类型分为根节点、内部节点和叶子节点三种，内部结点不存储数据，只存储关键字和子树指针，它只是叶子节点的映像，所以本身可以跟叶子节点中的关键字重复。叶子节点存储了所有的关键字和数据。
• 根节点和内部节点中，子树指针和关键字的数量相同，每个关键字都有一个对应的子树指针，关键字等于其子树中最大(或最小)的关键字，所有节点中的关键字都是按照关键字大小排列的。
• 根节点中关键字的数量m是： 
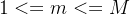
• 内部节点中关键字的数量m是：。
• 叶子节点之间通过双向链表排列了起来。

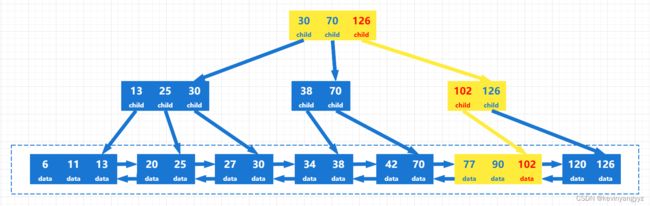
一个M为3的B+树如下图所示：

查找操作

在B+树中查找一个关键字都是从根节点开始的，而且为了减少一次磁盘IO，根节点一般都缓存在内存里面，Mysql会维护内存中的根节点和磁盘中的根节点的一致性。

简单的查找操作一般分为两种类型，一种是等值查找，一种是范围查找，我们分别来讨论这两种。

等值查找

假设我们要查找关键字为102的记录，我们先看下面这张图片中查找的过程，以有一个直观的认识，黄色表示可能扫描到的数据，红色表示命中的数据：

查找首先是在根节点中开始的。本例中B+树的关键字的子树指针，指向的是子树中最大的关键字，所以每一个子树指针的范围为：(前一个关键字,当前关键字]。

102落在(70,126]内，所以它需要在126的子树中继续查找。接下来在子树中找到了102这个关键字，但该子树节点并不是叶子节点(前面讲B+树定义的时候讲过，内部节点只是叶子节点的映像，所以最终到达叶子节点时，才能找到真正的数据)，接着往下层找，最终在102子树下的叶子节点命中了该关键字。

下面的伪代码简要描述了查询的基本步骤，在实际的算法中，应是采用二分查找在节点中查找关键字的，这里只是为了说明过程。

String findKey(String key, BpTree node){
    int i = 0;
    while(i < node.keys.length && key > node.keys[i]){
        i++;
    }
    //这个关键字大于了节点中所有关键字的大小，结束查找
    if(i == node.keys.length){
        return null;
    }
    //当节点为叶子节点时，命中
    if(key == node.keys[i] && node.keys[i].isLeaf){
        return node.keys[i];
    }
    //到达叶子节点还未命中，结束查找
    if(node.keys[i].isLeaf)
        return null;
    //从子树中继续递归查找
    return findKey(key, node.keys[i].child);
}

范围查找

范围查找是B+树的优势之一，比如要查找[20,30]之间的数据，只需要先找到20关键字，然后跟着叶子节点的链表指针向后遍历，直至>30为止，整个过程如下图所示。(也可以先找30，再向前遍历)

 特别是在查找Max值时，只需要找到根节点中最大的关键字即可。相反，如果关键字的子树指针指向的是子树中最小的关键字，那么查找Min也同样。

插入操作

和其他的平衡树一样，B+树在插入或者删除关键字的同时，都要保证其作为B+树的基本性质。

在B+树中的节点的关键字数量等于M时，我们称之为满节点，关键字大于满节点时就需要进行分裂操作。没错，B+树层数的增加是通过分裂完成的，接下来你将看到这点。

插入之前需要先通过查找操作找到该关键字所属的叶节点，如果叶节点满了则执行分裂操作，将其分为两个节点，并将两个节点的最大节点上升至父节点，如果父节点也满了则需要继续往上分裂，直至没有满节点为止。

假设我们要插入12，整个过程如图a(1-3)所示：

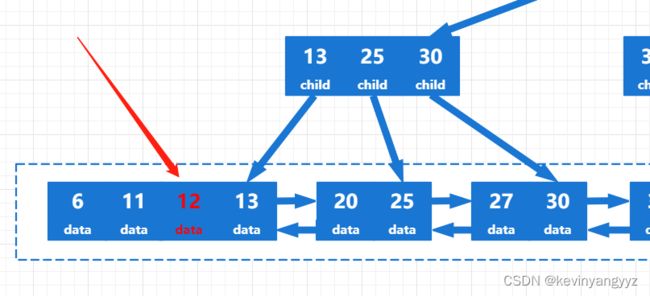图a-1

 首先通过查找操作找到了12应该插入的叶节点，并将它插入了节点中。但由于4个关键字已经大于满节点的数量，所以需要分裂操作，如图a-2所示。

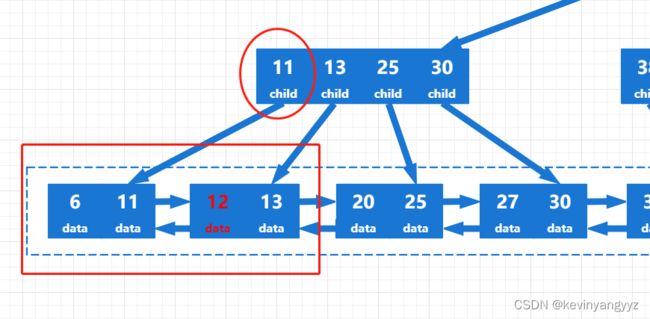图a-2

 图a.2中12所插入的叶节点被分成了两个，分裂之后的左节点最大关键字是11，所以它的父节点必须增加一个11的映像。正如你所看到的，父节点也溢出了，所以需要继续分裂，分裂之后最终的B+树如图a.3所示。

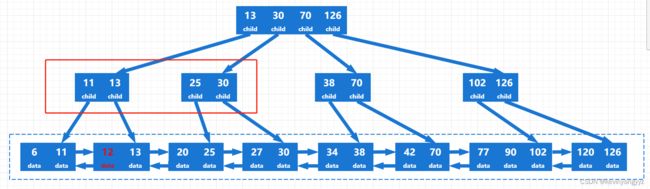图a-3

 需要注意的，当叶子节点的最大关键字变化时，所有的上层也需要一起变化。比如插入200时，第一层和第二层的126都需要变成200。

删除操作

如果说插入操作需要保持节点不超满，那么删除操作就是要保持节点不超小。对应的超满是大于M，超小是小于。在咱们的例子中M=3，所有节点中关键字不能小于2。

假设我们要删除126，整个过程如图b(1-2)所示：

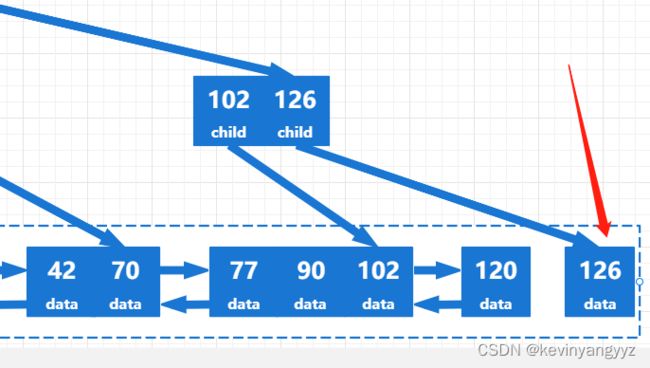图b-1

 删除126后该节点只剩下一个关键字，所以需要从兄弟节点中借一个关键字，形成2个节点，同时改变父节点，最终如图b-2所示：

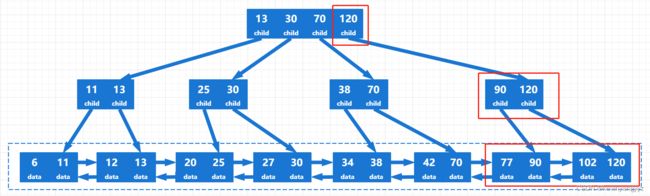图b-2

总结

到现在为止我们还没讲到B树，B+树是基于B树的，两者都适合作为数据库索引结构，但是Innodb最终选择了B+树，笔者认为有两个方面，一个是叶子节点通过链表链接了起来，比较适合范围查找，另一个是把数据指针都放在叶子节点上，在同等树高下，存储的数据量更多。

 下表对比了B树、B+树和红黑树，红黑树首先被排除在外了，比如同样2000w数据，M=1170的B+树树高只有3层左右，而红黑树则有24层：

对比项	B树	B+树	红黑树
数据指针存储位置	内部节点和叶子节点	叶子节点	所有节点
关键字数量m/节点			1
子树数量m/节点			2
叶子节点有链表	无	有	/