第一章,04-n阶行列式的几何意义
第一章,04-n阶行列式的几何意义
-
- 简介
- 几个特殊行列式
-
- 对角行列式
- 副对角行列式
- 上(下)三角行列式
- 几何意义
-
- 二阶行列式
-
- 转置矩阵
- 性质1
- 性质2
- 性质3
- 性质4
- 性质5
- 性质6
- 三阶行列式
-
- 性质1
- 性质2
- 性质3
- 性质4
简介
这是《玩转线性代数》的学习笔记
少壮不努力,老大徒伤悲,学校里没学好,工作多年后又从头看,两行泪。。。
几个特殊行列式
对角行列式
除主对角线外的其它元素都为零
∣ λ 1 ⋱ λ n ∣ \begin{vmatrix} \lambda_1\\ & \ddots & \\ & & \lambda_n \end{vmatrix} ∣∣∣∣∣∣λ1⋱λn∣∣∣∣∣∣
令 λ i = a i i \lambda_i=a_{ii} λi=aii:
∣ λ 1 ⋱ λ n ∣ = ∣ a 11 ⋱ a n n ∣ = Σ p 1 . . . p n ( − 1 ) t a 1 p 1 a 2 p 2 . . . a n p n \begin{vmatrix} \lambda_1\\ & \ddots & \\ & & \lambda_n \end{vmatrix}=\begin{vmatrix} a_{11}\\ & \ddots & \\ & & a_{nn} \end{vmatrix}=\Sigma_{p_1...p_n}(-1)^ta_{1p_1}a_{2p_2}...a_{np_n} ∣∣∣∣∣∣λ1⋱λn∣∣∣∣∣∣=∣∣∣∣∣∣a11⋱ann∣∣∣∣∣∣=Σp1...pn(−1)ta1p1a2p2...anpn
当 i ≠ j i\neq j i=j时, a i j = 0 a_{ij}=0 aij=0,因此只有对角线元素相乘项不为0,且符号为正。故原式 = λ 1 . . . λ n =\lambda_1...\lambda_n =λ1...λn
副对角行列式
除副对角线外的其它元素都为零
∣ λ 1 ⋯ λ n ∣ \begin{vmatrix} & & \lambda_1\\ & \cdots & \\ \lambda_n \end{vmatrix} ∣∣∣∣∣∣λn⋯λ1∣∣∣∣∣∣
令 λ i = a i ( n − i + 1 ) \lambda_i=a_{i(n-i+1)} λi=ai(n−i+1):
∣ λ 1 ⋯ λ n ∣ = ∣ a 1 n ⋯ a n 1 ∣ = Σ p 1 . . . p n ( − 1 ) t a 1 p 1 a 2 p 2 . . . a n p n = ( − 1 ) τ [ n ( n − 1 ) − 321 ] a 1 n a 2 ( n − 1 ) ⋯ a n 1 = ( − 1 ) 1 2 n ( n − 1 ) λ 1 . . . λ n \begin{vmatrix} & & \lambda_1\\ & \cdots & \\ \lambda_n \end{vmatrix}=\begin{vmatrix} & & a_{1n}\\ & \cdots & \\ a_{n1} \end{vmatrix}=\Sigma_{p_1...p_n}(-1)^ta_{1p_1}a_{2p_2}...a_{np_n} =(-1)^{\tau[n(n-1)-321]}a_{1n}a_{2(n-1)}\cdots a_{n1}=(-1)^{\frac{1}{2}n(n-1)}\lambda_1...\lambda_n ∣∣∣∣∣∣λn⋯λ1∣∣∣∣∣∣=∣∣∣∣∣∣an1⋯a1n∣∣∣∣∣∣=Σp1...pn(−1)ta1p1a2p2...anpn=(−1)τ[n(n−1)−321]a1na2(n−1)⋯an1=(−1)21n(n−1)λ1...λn
上(下)三角行列式
主对角线以下(上)的元素全为0,称为上(下)三角行列式,以上三角为例:
D = ∣ a 11 a 12 ⋯ a 1 n 0 a 22 ⋯ a 2 n 0 0 ⋯ ⋯ ⋮ ⋮ ⋱ ⋮ 0 0 0 a n m ∣ D=\begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ 0 & a_{22} & \cdots & a_{2n} \\ 0 & 0 & \cdots & \cdots \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & a_{nm} \end{vmatrix} D=∣∣∣∣∣∣∣∣∣∣∣a1100⋮0a12a220⋮0⋯⋯⋯⋱0a1na2n⋯⋮anm∣∣∣∣∣∣∣∣∣∣∣
不含0的项只有对角线,因此 D = a 11 a 22 ⋯ a n n D=a_{11}a_{22}\cdots a_{nn} D=a11a22⋯ann。
几何意义
对二阶行列式 D = ∣ a 1 a 2 b 1 b 2 ∣ D=\begin{vmatrix} a_{1} & a_{2} \\ b_{1} & b_{2} \\ \end{vmatrix} D=∣∣∣∣a1b1a2b2∣∣∣∣,把每一行都当成一个向量,记为 a = ( a 1 , a 2 ) , b = ( b 1 , b 2 ) a=(a_1,a_2),b=(b_1,b_2) a=(a1,a2),b=(b1,b2), α , β \alpha,\beta α,β为向量 a , b a,b a,b与x轴的顺时针方向的夹角,黄色部分为向量 a 、 b a、b a、b张成的平行四边形,其中 ∣ ∣ a ∣ ∣ ∣ ∣ b ∣ ∣ {||a|| \ ||b ||} ∣∣a∣∣ ∣∣b∣∣为向量 a , b a,b a,b的长度,见下图(来源):
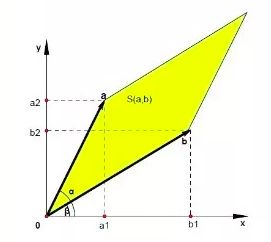
则有:
∣ a 1 a 2 b 1 b 2 ∣ = a 1 b 2 − a 2 b 1 = ∣ ∣ a ∣ ∣ ∣ ∣ b ∣ ∣ ∣ ∣ a ∣ ∣ ∣ ∣ b ∣ ∣ ( a 1 b 2 − a 2 b 1 ) = ∣ ∣ a ∣ ∣ ∣ ∣ b ∣ ∣ ( b 2 ∣ ∣ b ∣ ∣ a 1 ∣ ∣ a ∣ ∣ − b 1 ∣ ∣ b ∣ ∣ a 2 ∣ ∣ a ∣ ∣ ) = ∣ ∣ a ∣ ∣ ∣ ∣ b ∣ ∣ s i n ( β − α ) = S ( a , b ) ( S ( a , b ) 表 示 以 a , b 为 边 的 平 行 四 边 形 的 面 积 ) \begin{vmatrix} a_{1} & a_{2} \\ b_{1} & b_{2} \\ \end{vmatrix} =a_1b_2-a_2b_1 =\frac{||a|| \ ||b ||}{||a|| \ ||b ||} (a_1b_2-a_2b_1) =||a|| \ ||b || (\frac{b_2}{||b||} \frac{a_1}{||a||} - \frac{b_1}{||b||} \frac{a_2}{||a||}) =||a|| \ ||b || sin(\beta - \alpha)=S(a,b) \quad (S(a,b)表示以a,b为边的平行四边形的面积) ∣∣∣∣a1b1a2b2∣∣∣∣=a1b2−a2b1=∣∣a∣∣ ∣∣b∣∣∣∣a∣∣ ∣∣b∣∣(a1b2−a2b1)=∣∣a∣∣ ∣∣b∣∣(∣∣b∣∣b2∣∣a∣∣a1−∣∣b∣∣b1∣∣a∣∣a2)=∣∣a∣∣ ∣∣b∣∣sin(β−α)=S(a,b)(S(a,b)表示以a,b为边的平行四边形的面积)
二阶行列式
可以看到行列式符号与 s i n ( β − α ) sin(\beta - \alpha) sin(β−α)相同,即 S ( a , b ) S(a,b) S(a,b)不一定为正数,因此将 S ( a , b ) S(a,b) S(a,b)称为 有 向 面 积 {\color{BurntOrange} 有向面积} 有向面积。
转置矩阵
记 D = ∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ∣ D=\begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix} D=∣∣∣∣∣∣∣∣∣a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann∣∣∣∣∣∣∣∣∣,把此行列式沿主对角线翻转(行列对换),称为D的转置,记为 D T D^T DT:
D T = ∣ a 11 a 21 ⋯ a n 1 a 12 a 22 ⋯ a n 2 ⋮ ⋮ ⋱ ⋮ a 1 n a 2 n ⋯ a n n ∣ D^T=\begin{vmatrix} a_{11} & a_{21} & \cdots & a_{n1} \\ a_{12} & a_{22} & \cdots & a_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{nn} \end{vmatrix} DT=∣∣∣∣∣∣∣∣∣a11a12⋮a1na21a22⋮a2n⋯⋯⋱⋯an1an2⋮ann∣∣∣∣∣∣∣∣∣
性质1
互换两行或两列,符号改变
可以从面积出发:
∣ a 1 a 2 b 1 b 2 ∣ = S ( a , b ) = ∣ ∣ a ∣ ∣ ∣ ∣ b ∣ ∣ s i n ( β − α ) = − ∣ ∣ b ∣ ∣ ∣ ∣ a ∣ ∣ s i n ( α − β ) = − S ( b , a ) = − ∣ b 1 b 2 a 1 a 2 ∣ \begin{vmatrix} a_1 & a_2\\b_1 & b_2 \end{vmatrix} =S(a,b)=||a|| \ ||b||sin(\beta-\alpha) =-||b||\ ||a||sin(\alpha-\beta)=-S(b,a) =-\begin{vmatrix} b_1 & b_2\\a_1 & a_2 \end{vmatrix} ∣∣∣∣a1b1a2b2∣∣∣∣=S(a,b)=∣∣a∣∣ ∣∣b∣∣sin(β−α)=−∣∣b∣∣ ∣∣a∣∣sin(α−β)=−S(b,a)=−∣∣∣∣b1a1b2a2∣∣∣∣
也可以从定义出发:
∣ a 1 a 2 b 1 b 2 ∣ = a 1 b 2 − a 2 b 1 \begin{vmatrix} a_{1} & a_{2} \\ b_{1} & b_{2} \\ \end{vmatrix} =a_1b_2-a_2b_1 ∣∣∣∣a1b1a2b2∣∣∣∣=a1b2−a2b1
∣ b 1 b 2 a 1 a 2 ∣ = a 2 b 1 − a 1 b 2 = − ∣ a 1 a 2 b 1 b 2 ∣ \begin{vmatrix} b_{1} & b_{2} \\ a_{1} & a_{2} \\ \end{vmatrix} =a_2b_1-a_1b_2 =-\begin{vmatrix} a_{1} & a_{2} \\ b_{1} & b_{2} \\ \end{vmatrix} ∣∣∣∣b1a1b2a2∣∣∣∣=a2b1−a1b2=−∣∣∣∣a1b1a2b2∣∣∣∣
性质2
k ∣ a 1 a 2 b 1 b 2 ∣ = ∣ k a 1 k a 2 b 1 b 2 ∣ = ∣ a 1 a 2 k b 1 k b 2 ∣ k\begin{vmatrix} a_{1} & a_{2} \\ b_{1} & b_{2} \\ \end{vmatrix} =\begin{vmatrix} ka_{1} & ka_{2} \\ b_{1} & b_{2} \\ \end{vmatrix} =\begin{vmatrix} a_{1} & a_{2} \\ kb_{1} & kb_{2} \\ \end{vmatrix} k∣∣∣∣a1b1a2b2∣∣∣∣=∣∣∣∣ka1b1ka2b2∣∣∣∣=∣∣∣∣a1kb1a2kb2∣∣∣∣,k为任意实数。
如下图(来源)所示,可见有向面积扩大至k倍:
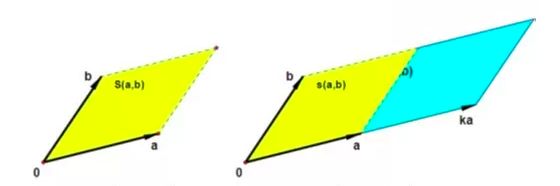
因有 k ∣ a 1 a 2 b 1 b 2 ∣ = k S ( a , b ) = S ( k a , b ) = ∣ k a 1 k a 2 b 1 b 2 ∣ k\begin{vmatrix} a_{1} & a_{2} \\ b_{1} & b_{2} \\ \end{vmatrix} =kS(a,b)=S(ka,b) =\begin{vmatrix} ka_{1} & ka_{2} \\ b_{1} & b_{2} \\ \end{vmatrix} k∣∣∣∣a1b1a2b2∣∣∣∣=kS(a,b)=S(ka,b)=∣∣∣∣ka1b1ka2b2∣∣∣∣
性质3
∣ a 1 a 2 b 1 + c 1 b 2 + c 2 ∣ = ∣ a 1 a 2 b 1 b 2 ∣ + ∣ a 1 a 2 c 1 c 2 ∣ \begin{vmatrix} a_{1} & a_{2} \\ b_{1}+c_{1} & b_{2} +c_{2}\\ \end{vmatrix} =\begin{vmatrix} a_{1} & a_{2} \\ b_{1} & b_{2} \\ \end{vmatrix} +\begin{vmatrix} a_{1} & a_{2} \\ c_{1} & c_{2} \\ \end{vmatrix} ∣∣∣∣a1b1+c1a2b2+c2∣∣∣∣=∣∣∣∣a1b1a2b2∣∣∣∣+∣∣∣∣a1c1a2c2∣∣∣∣
如下图(来源)所示:

可见 S ( a , b + c ) = S ( a , b ) + S ( a , c ) S(a,b+c)=S(a,b)+S(a,c) S(a,b+c)=S(a,b)+S(a,c)
性质4
∣ a 1 a 2 k a 1 k a 2 ∣ = 0 \begin{vmatrix} a_{1} & a_{2} \\ ka_{1} & ka_{2} \\ \end{vmatrix}=0 ∣∣∣∣a1ka1a2ka2∣∣∣∣=0
同向向量共线,有向面积为0:

性质5
∣ a 1 a 2 b 1 b 2 ∣ = ∣ a 1 a 2 b 1 + λ a 1 b 2 + λ a 2 ∣ \begin{vmatrix} a_{1} & a_{2} \\ b_{1} & b_{2} \\ \end{vmatrix} =\begin{vmatrix} a_{1} & a_{2} \\ b_{1}+\lambda a_1 & b_{2}+\lambda a_2\\ \end{vmatrix} ∣∣∣∣a1b1a2b2∣∣∣∣=∣∣∣∣a1b1+λa1a2b2+λa2∣∣∣∣
即将某行的常数倍加到另一行上,行列式值不变。
从下图可见,实际为将四边形沿a方向拉伸,底边和高都不变,因此面积不变:
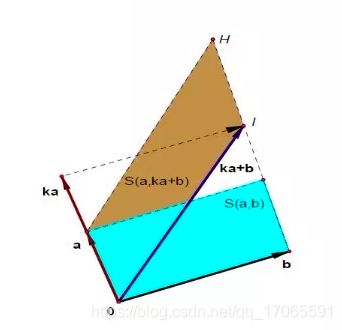
性质6
转置行列式与原行列式相等
由定义可证:
∣ a 1 a 2 b 1 b 2 ∣ = a 1 b 2 + a 2 b 1 ∣ a 1 b 1 a 2 b 2 ∣ = a 1 b 2 + a 2 b 1 \begin{vmatrix} a_{1} & a_{2} \\ b_{1} & b_{2} \\ \end{vmatrix} =a_1b_2+a_2b_1\\ \begin{vmatrix} a_{1} & b_1 \\ a_2 & b_{2} \end{vmatrix}=a_1b_2+a_2b_1 ∣∣∣∣a1b1a2b2∣∣∣∣=a1b2+a2b1∣∣∣∣a1a2b1b2∣∣∣∣=a1b2+a2b1
即 D T = D D^T=D DT=D
(也可以通过有向面积相等得到)
三阶行列式
三阶行列式的值是由其行向量或列向量按顺序所张成的平行六面体的有向体积,以原行或列的排列为标准次序,任意两个向量的顺序改变一次符号变化一次。
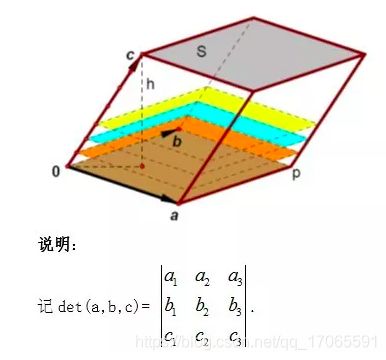
性质1
d e t ( a , b , c + d ) = d e t ( a , b , c ) + d e t ( a , b , d ) det(a,b,c+d)=det(a,b,c)+det(a,b,d) det(a,b,c+d)=det(a,b,c)+det(a,b,d)
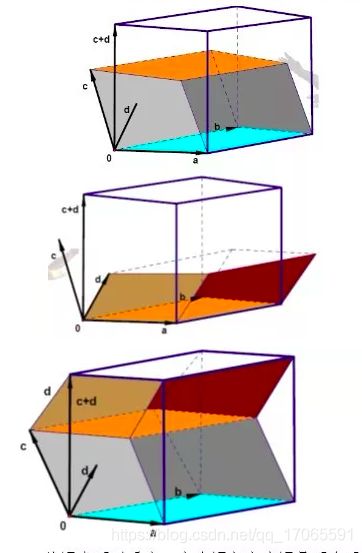
性质2
d e t ( a , a , c ) = 0 det(a,a,c)=0 det(a,a,c)=0
只要含同向向量,det一定为0:
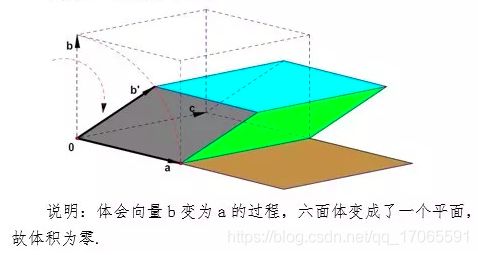
性质3
k d e t ( a , b , c ) = d e t ( k a , b , c ) = d e t ( a , k b , c ) = d e t ( a , b , k c ) kdet(a,b,c)=det(ka,b,c)=det(a,kb,c)=det(a,b,kc) kdet(a,b,c)=det(ka,b,c)=det(a,kb,c)=det(a,b,kc)
任意一个向量长度变化,体积也跟着发生同比例的变化:
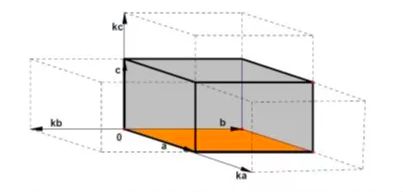
性质4
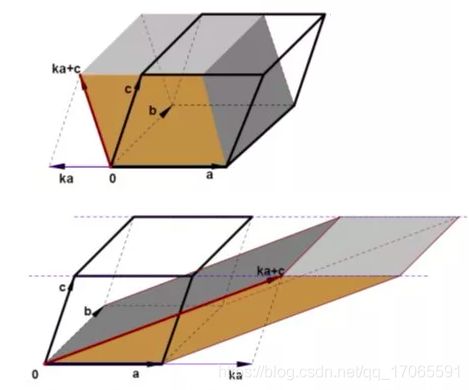
d e t ( a , b , c ) = d e t ( a , b , k a + c ) det(a,b,c)=det(a,b,ka+c) det(a,b,c)=det(a,b,ka+c)
将某行的k倍加到另一行行列式值不变,与二阶行列式性质5类似,为沿某个方向拉伸: