【刷题之路Ⅱ】LeetCode 739. 每日温度
【刷题之路Ⅱ】LeetCode 739. 每日温度
- 一、题目描述
- 二、解题
-
- 1、方法1——暴力法
-
- 1.1、思路分析
- 1.2、代码实现
- 2、方法2——单调栈
-
- 2.1、思路分析
- 2.2、先将栈实现一下
- 2.3、代码实现
一、题目描述
原题连接: 739. 每日温度
题目描述:
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]
提示:
1 <= temperatures.length <= 105
30 <= temperatures[i] <= 100
二、解题
1、方法1——暴力法
1.1、思路分析
大家应该最容易想到的就是暴力法,对于每一个temperatures[i],我们都令j == i + 1 开始查找,只要找到一个temperatures[j] > temperatures[i]我们就可以退出,并记录j - i进一个答案数组。
1.2、代码实现
有了以上思路,那我们写起代码来也就水到渠成了:
int* dailyTemperatures(int* temperatures, int temperaturesSize, int* returnSize) {
assert(temperatures && returnSize);
*returnSize = temperaturesSize;
int *answer = (int*)malloc(temperaturesSize * sizeof(int));
if (NULL == answer) {
perror("malloc fail!\n");
exit(-2);
}
memset(answer, 0, temperaturesSize * sizeof(int));
int i = 0;
int j = 0;
for (i = 0; i < temperaturesSize - 1; i++) {
for (j = i + 1; j < temperaturesSize; j++) {
if ( temperatures[j] > temperatures[i]) {
answer[i] = j - i;
break;
}
}
}
return answer;
}
// 时间复杂度:O(n^2),n即为数组长度。
// 空间复杂度:O(n),我们需要n个整型空间来存储答案数组,故空间复杂度为O(n)。
(只不过这种复杂度在LeetCode上是过不了的)
2、方法2——单调栈
2.1、思路分析
可能做过496. 下一个更大元素 I的朋友们就会发现这两题是这么的相似。
确实,这两题同样是往右边找更大的元素,只不过这一题相比于496题来说更简便一些,因为这一题只是在一个数组中查找,而496题却是要两个数组中查找。
所以这一题当然也能用496题的单调栈的思路,但相比于496题这题的单调栈的思路就会更简单一点,因为496题涉及到两个数组,所以496题还需要借助哈希表来映射,但这一题就只需要一个栈即可。
接下来看思路:
我们可以创建一个存储下标的栈,然后顺序遍历数组,当栈为空时,就将遍历到的元素的下标入栈:
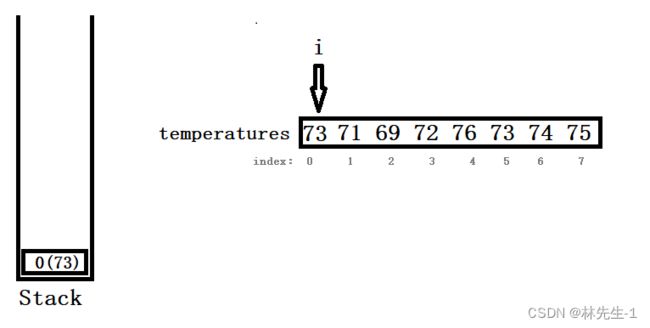
(括号内为对应的温度)
而当遍历到的温度小于栈顶温度时,就将当前遍历到的下标压入栈中:
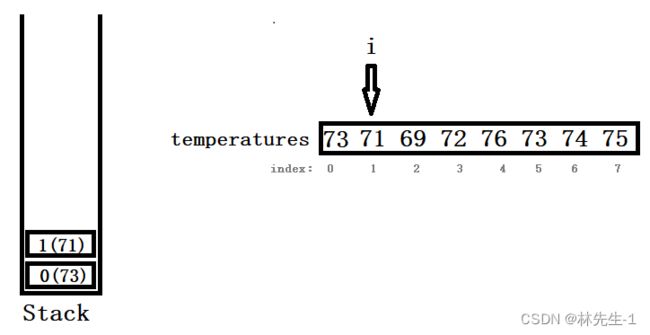
所以如果栈中有所个下标,那么这些下标对应的温度一定是自顶向下递增的:

这也正是为什么这个方法称之为“单调栈”的原因。
而当遍历到的温度大于栈顶下标对应的温度时,我们需要连续地将栈顶下标取出,记为index,连续的当前遍历到的温度是否大于index所对应的温度,如果大于就将栈顶下标弹出栈,并将答案数组的answer[index]赋值为i - index。
重复上述操作直到,当前遍历到的温度不在大于栈顶温度或者栈为空。最后再将当前遍历到的温度的下标入栈:
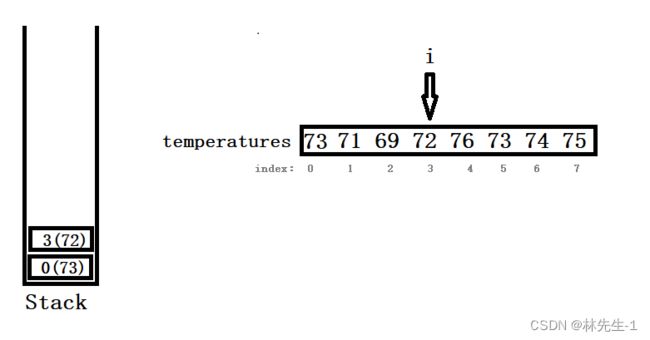
这样但我们遍历完了数组,我们的答案也就出来了。
2.2、先将栈实现一下
先将栈CV一下:
// 重定义数据类型
typedef int DataType;
// 定义栈结构
typedef struct stack {
DataType* data;
int top;
int capacity;
} Stack;
// 栈的初始化
void StackInit(Stack* ps);
// 压栈
void StackPush(Stack* ps, DataType x);
// 弹栈
void StackPop(Stack* ps);
// 返回栈顶数据
DataType StackTop(Stack* ps);
// 返回栈的数据个数
int StackSize(Stack* ps);
// 判断栈是否为空
bool StackEmpty(Stack* ps);
// 栈的销毁
void DestroyStack(Stack* ps);
// 栈的初始化
void StackInit(Stack* ps) {
assert(ps);
ps->data = NULL;
ps->top = 0;
ps->capacity = 0;
}
// 压栈
void StackPush(Stack* ps, DataType x) {
assert(ps);
// 检查是否需要增容
if (ps->top == ps->capacity) {
int newCapacity = ps->capacity == 0 ? 10 : ps->capacity * 2;
DataType* temp = (DataType*)realloc(ps->data, newCapacity * sizeof(DataType));
if (NULL == temp) {
perror("ralloc fail!\n");
exit(-1);
}
ps->data = temp;
ps->capacity = newCapacity;
}
ps->data[ps->top] = x;
ps->top++;
}
// 弹栈
void StackPop(Stack* ps) {
assert(ps);
assert(ps->top > 0);
ps->top--;
}
// 返回栈顶数据
DataType StackTop(Stack* ps) {
assert(ps);
assert(!StackEmpty(ps));
return ps->data[ps->top - 1];
}
// 返回栈的数据个数
int StackSize(Stack* ps) {
assert(ps);
assert(ps->top >= 0);
return ps->top;
}
// 判断栈是否为空
bool StackEmpty(Stack* ps) {
assert(ps);
return ps->top == 0;
}
// 栈的销毁
void DestroyStack(Stack* ps) {
assert(ps);
free(ps->data);
ps->data = NULL;
ps->top = 0;
ps->capacity = 0;
}
2.3、代码实现
有了以上思路,那我们写起代码来也就水到渠成了:
int* dailyTemperatures(int* temperatures, int temperaturesSize, int* returnSize) {
assert(temperatures && returnSize);
*returnSize = temperaturesSize;
int i = 0;
int *answer = (int*)malloc(temperaturesSize * sizeof(int));
if (NULL == answer) {
perror("malloc fail!\n");
exit(-1);
}
memset(answer, 0, temperaturesSize * sizeof(int));
Stack stack;
StackInit(&stack);
int index = 0;
for (i = 0; i < temperaturesSize; i++) {
if (!StackEmpty(&stack)) {
index = StackTop(&stack);
}
if (StackEmpty(&stack)) {
StackPush(&stack, i);
} else if (temperatures[i] > temperatures[index]) {
while (!StackEmpty(&stack)) {
index = StackTop(&stack);
if (temperatures[i] > temperatures[index]) {
answer[index] = i - index;
StackPop(&stack);
} else {
break;
}
}
StackPush(&stack, i);
} else {
StackPush(&stack, i);
}
}
DestroyStack(&stack);
return answer;
}
时间复杂度:O(n),n为数组长度,我们需要顺序遍历一遍数组,而每一个下标最多也只有一次出栈和进栈的机会,故总的时间复杂度还是O(n)。
空间复杂度:O(n),最坏情况下,n - 1个温度都会累积在栈中,故空间复杂度为O(n)。