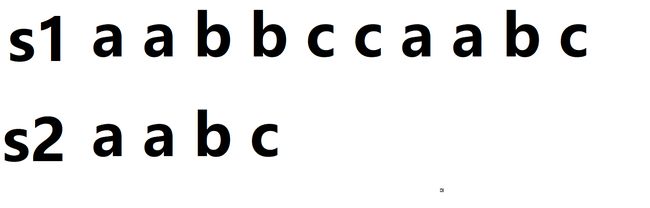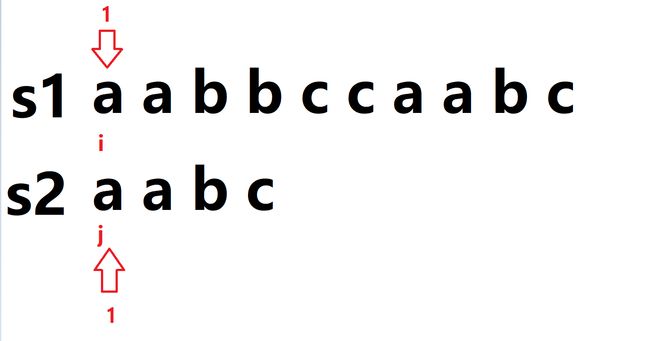学习分享-字符串匹配—KMP算法

什么是KMP算法？

• KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n) 。

• 其中KMP算法的核心：next()函数的实现过程。next(）函数用来记录最长相等前后缀长度。

• KMP算法的运用场景：进行字符串匹配。

字符串匹配的暴力做法

当给你一个字符串S1="aabbccaabc" ; S2="aabc"，在这里S1我称为匹配的串（长的串），S2称为模板串(短的串)，现在这两个字符进行匹配，你是如何做的呢？

在没有KMP算法之前，我们是如何进行字符串匹配的呢？毫不意外的就是咱们最熟悉的模拟暴力算法进行解决。

我们定义两个指针，一个用来指向S1，另一个指向S2，在这里我定义他们的下标都是从1开始的，也可以从0开始，这个是看个人习惯的。同时定义两个数组来记录，S[N],P[M],S[N]是用来储存S1字符串,P[M]是用来存储S2字符串，下面我们就来进行暴力做法叭，好嘞，上代码！

char S[N],P[M];
cin>>S>>P;
for(int i = 1 ; i <= strlen(S) ; i++ ){
    bool flag = true;
    for(int j = 1 ; j <= strlen(P) ; j++)
    {
        if(P[j] != S[i+j-1]){
            flag = false;
            break;
        }
    }
}      

上面就是主要的代码部分，但是这里的复杂度是多少呢？O（n*m），这样一看感觉并没有什么，但是当处理10^6*10^6的话就会特别大，所以如何进行优化呢？

暴力算法优化（next数组）

我们先来思考一下问题？怎么处理数据优化。

• 减少数据的重复使用（即减少重复比较）

• S2字符串如何往后退，退出多少才是最合适的。

这里我们就要引出咱们KMP算法的精髓之笔：next[]数组

看到这里，你或许会纳闷这next[]数组究竟是什么东西，这玩意有什么用？

next[]数组✋

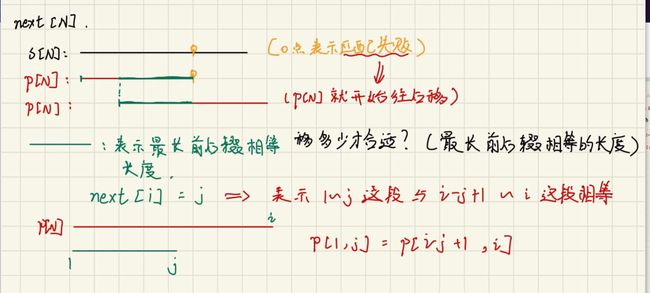
next[]是用来存储最长前后缀相等的长度。

先来讲一下什么是前后缀，前缀是不包含最后一个字符的前缀串，比如我们给定S="aabbc",现在我们求一下这个字符串的前缀有哪些（如下所示）

• a

• aa

• aab

• aabb

后缀是不包含最开始的第一个字符的后缀串,那这个S的后缀有哪些呢（如下所示）

• c

• bc

• bbc

• abbc

如果一个字符串只包含一个字符呢？它有前缀和后缀么，答案是没有。当给定一个字符串S="a"的话，他的前缀和后缀是没有的，不存在的。

了解了什么是前后缀，那么我们来试着给个例子来求一下next[]数组叭

给定一个字符串P="abababab",我们求一下next数组分别是多少

• next[1] = 0;

• next[2] = 0 ;

• next[3] = 1;

• next[4] = 2;

• next[5] = 3;

• next[6] = 4;

• next[7] = 5;

• next[8] = 6;

相信看到现在的小伙伴，已经了解到了next数组的含义了，下面来实现一下如何进行next数组实现的过程

const int N = 1000010;
char p[N],s[M];
int next[N];
cin>>p+1>>s+1;//这里p+1,s+1是为了让数组下标从1开始，如果不加则数组下标从0开始即可
for(int i = 2 , j = 0 ; i <= strlen(p) ; i++） //这里i=2开始,i=1的话next[1]是等于0的，不需要考虑
{
    while(j&&p[i]!=p[j+1]) j = next[j];//如果不匹配则j回溯往前寻找
    if(p[i]==p[j+1]) j++;
    next[i] = j;//开始记录最长相等前后缀长度
}

KMP匹配过程

KMP匹配过程跟next数组实现是相似的，话不多说，老板直接上代码！

//进行KMP匹配过程
for(int i = 1 , j = 0; i <= strlen(s) ; i++)//这里定义i=1,j=0，要注意匹配的时候是i与j+1比较，j=0是因为刚开始next[1]=0的；
{
    while(j&&s[i]!=p[j+1]) j = next[j]; //如果不匹配或且j还可以回溯， j继续回溯 ；j = next[j]
    if(s[i]==p[j+1]) j++;
    if(j==strlen(p))//如果匹配成功
    {
        cout<

整体KMP代码实现

const int N = 1000010;
char p[N],s[M];
int next[N];
cin>>p+1>>s+1;//这里p+1,s+1是为了让数组下标从1开始，如果不加则数组下标从0开始即可
//next数组实现过程
for(int i = 2 , j = 0 ; i <= strlen(p) ; i++） //这里i=2开始,i=1的话next[1]是等于0的，不需要考虑
{
    while(j&&p[i]!=p[j+1]) j = next[j];//如果不匹配则j回溯往前寻找
    if(p[i]==p[j+1]) j++;
    next[i] = j;//开始记录最长相等前后缀长度
}
//kmp匹配过程
for(int i = 1 , j = 0; i <= strlen(s) ; i++)//这里定义i=1,j=0，要注意匹配的时候是i与j+1比较，j=0是因为刚开始next[1]=0的；
{
    while(j&&s[i]!=p[j+1]) j = next[j]; //如果不匹配或且j还可以回溯， j继续回溯 ；j = next[j]
    if(s[i]==p[j+1]) j++;
    if(j==strlen(p))//如果匹配成功
    {
        cout<

例题部分

拿luogu的一道题目进行KMP代码实现

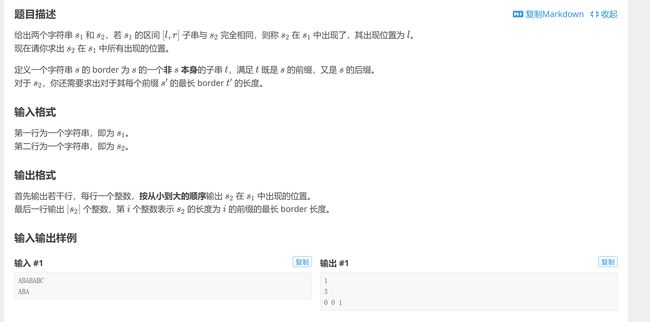
洛谷例题-P3375 【模板】KMP字符串匹配

#include
#include
using namespace std;
const int N=1000010;
char s[N],p[N];
int ne[N];
int main(){
    cin>>s+1>>p+1;
    int s_len,p_len;
    s_len = strlen(s+1);
    p_len = strlen(p+1);
    //求next过程.也就是题目要求的border的长度
    for(int i=2 , j = 0 ; i<= p_len ; i++){
        while(j&&p[i]!=p[j+1]) j = ne[j];
        if(p[i]==p[j+1]) j++;
        ne[i] = j;
    }
    //kmp过程
    for(int i = 1 , j = 0 ; i <= s_len ; i++){
        while(j&&p[j+1]!=s[i]) j = ne[j];
        if(p[j+1]==s[i]) j++;
        //匹配是否完成
        if(j==p_len){
            cout<