西工大校赛2 weekly contest 10.16

西工大校赛2 weekly contest 10.16

[Problems - Codeforces.pdf](assets/Problems - Codeforces-20221019121149-0g83yz5.pdf)

校赛网址：https://codeforces.com/contestInvitation/8753eda10ddfb07a491cb46131bc666c313fde60

A Tree Factory

​

题解

这是一个2500的题目。

这道题目是一道构造题目

构造题目有一个较为套路的解题方法：

1. 寻找答案的一个下界。
2. 证明存在一种方法来达到这一种下界。

同时结合逆向思考

NO1.

原问题是对于一个节点，其父亲也是非根节点，把非根节点变成他爷爷的儿子。

倒过来想就是：对于任意一个节点，我可以把它的两个儿子一个变成另一个的儿子。

注意这一种操作，每进行一次操作，最多使得树的深度+1（也有可能没有变化）

而最终的竹子的深度为n，假设现在这一课树的深度是dep，那么操作次数的一个下界就是$n-dep$

$NO2.$

我们找到深度最大的一个节点，从这一个节点开始，进行合并。

详细思路见代码

代码

#include 
using namespace std;
#define N 100050
set<int> son[N];//使用set，兼顾效率（频繁地移动）以及直观（儿子的个数是不是为1）
int fa[N];//父亲节点
int n;
int maxpos = 0, maxdep = 0;//记录深度最大的位置以及最大深度
//其实也可以存在数组里面，在建树的时候就可以得到
vector<int> op;
void getdep(int x, int d)
{
    if(d > maxdep){
        maxdep = d;
        maxpos = x;
    }
    for(const int &y : son[x])
    {
        getdep(y, d+1);
    }
}

void dfs(int x)
{
    if(x == 0) return;
    if(son[fa[x]].size() == 1) dfs(fa[x]);
    else
    {
        son[fa[x]].erase(x);
        int t = *son[fa[x]].begin();
        fa[x] = t;
        son[t].insert(x);
        op.push_back(x);
        dfs(x);
    }
}

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n-1; i++)
    {
        int t;
        scanf("%d", &t);
        son[t].insert(i);
        fa[i] = t;
    }
    getdep(0, 1);
    dfs(maxpos);
        int u = 0;
    while(son[u].size()){
        printf("%d ",u);
        u = *son[u].begin();
    }
    printf("%d\n",u);
    printf("%d\n", n - maxdep);
    for(int i = op.size()-1; i >= 0; i--){//要注意输出的顺序
        printf("%d ", op[i]);
    }
    return 0;
}

B Hotelier

​

题解

扫一遍就好，但是一定要注意包含0

代码

#include 
using namespace std;
#define N 100020
int n;
char a[N];
bool ans[10];
inline void L()
{
    int p = 0;
    while(ans[p]) p++;
    ans[p] = 1;
}
inline void R()
{
    int p = 9;
    while(ans[p]) p--;
    ans[p] = 1;
}
int main()
{
    scanf("%d", &n);
    scanf("%s", a+1);
    for(int i = 1; i <= n; i++)
    {
        if(a[i] == 'L') L();
        else if(a[i] == 'R') R();
        else {
            ans[a[i] - '0'] = false;
        }
    }
    for(int i = 0; i <= 9; i++){
        cout << ans[i];
    }
    return 0;
}

C

题解

这一道题目堪比水题，但是我还是想证明一下。

如果对于a以及b的最大公约数不是1，那么令$k=gcd(a,b)$，那么如图（红色表示被染成了白色！白色表示没有被染成白色）

现在，a与b是k的倍数。

容易知道：当a=k,b=k时，白色方块的集合一定包含a = a, b = b（原来的值）时的情况。

即使对于这样一个更大集合，采用第二，三种方法构建白色方块，并不会使得任何黑色方块变成白色的。所以黑色方块是无限个。

所以在原来的情况下，白色方块更少，黑色方块是无限个！

如果a以及b的最大公约数为1:

1. if i=0, it is colored white;
2. if i≥a and i−a is colored white, i is also colored white;
3. if i≥b and i−b is colored white, i is also colored white;
4. if i is still not colored white, it is colored black.

考虑1,2，4情况，（先忽略b的影响）。这样情况下，同样是

​

这种情况。

考虑3的影响。由于有$ax+by=1$，所以可以逐次向右，逐步增加染成白色的方块。最终全部是白色。

代码

#include 
using namespace std;
int main()
{
    int T;
    cin >> T;
    while(T--){
        int a, b;
        scanf("%d%d", &a, &b);
        if(__gcd(a, b) == 1) puts("Finite");
        else puts("Infinite");
    }
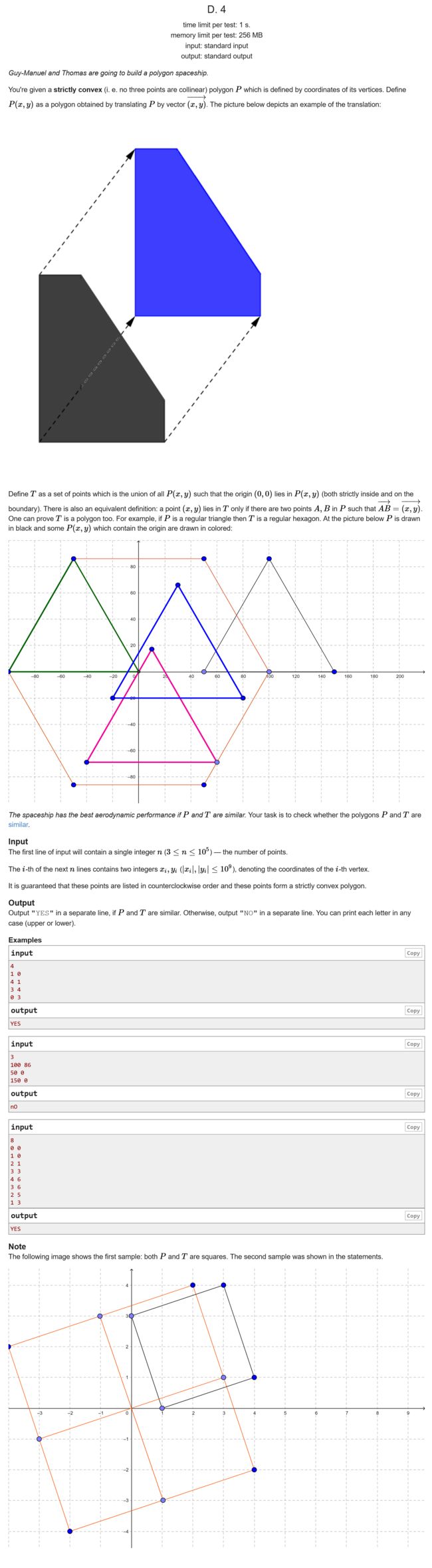
    return 0;
}

D Aerodynamic

​

相关词汇

convex 凸面的

hexagon 六边形

aerodynamic 空气动力学的

证明

网上的一些博文简直不付责任，仅凭“观察”…

官方题解

​

我的思路

首先，我们证明所生成的图形T是中心对称的。

假设 $p_1(x_1,y_1)$ 和 $p_2(x_2,y_2)$ 是两个点，对于T中的任意一个点$p_0(x_0,y_0)$，在P都可以找到两个点 $p_1,p_2$，使得这两个点的向量等与原点到$p_0$相等。这时候，把向量稍微反一下，这样，所生成的点就在$p_0$的对称处。

所以，T是中心对称的。

而由于必须要让P与T相似，所以要求原图形P是中心对称的。

如果要是原图形是中心对称的呢？

这个时候，把图形的对称中心置于原点，那么得到的T恰好是当前图形以原点为中心放大两倍。

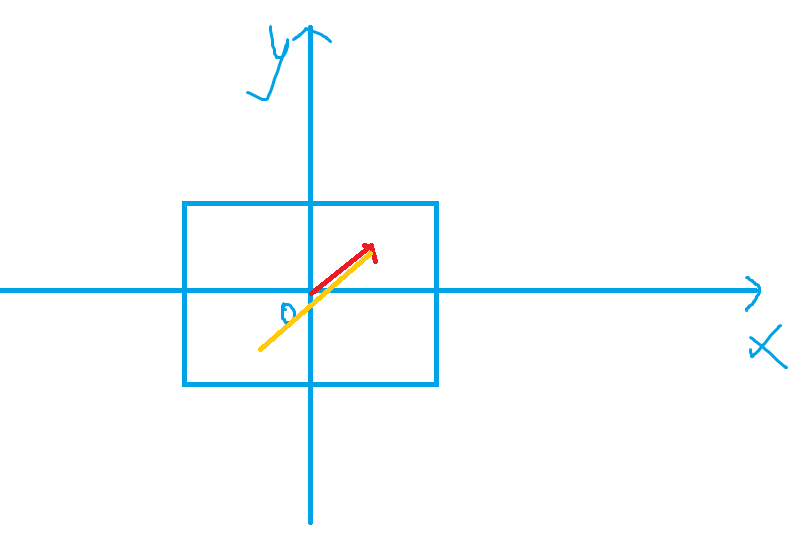
对于P中的点

可以这样操作，把黄色的线的一端放到原点，这样就可以证明原图形的一点$(x_0,y_0)$在生成的图形中就是$(2x_0,2y_0)$.

对于不在P中的点，那么其肯定与边界交于一点（通过旋转坐标系，把这样一条边与x轴平行，y = y1）

如果要生成$(2x_0,2y_0)$，但是原来的图形中的纵坐标之差一定小于2y1.故不可能在T中。

得证！

思路

经过上述的证明，现在的首要目标就是判断所给的图形是不是中心对称。

判断方法：

1. 首先，仅仅具有偶数个节点，才可以是中心对称图形。
2. 由于题目输入是严格的凸多边形，并且是按照逆时针进行输入的，所以我们可以根据随便对应的两个点找到对称中心。然后对于其他点，验证对称中心是不是选中的这这两个点。

代码

#include 
using namespace std;
#define N 100020
pair<int, int> a[N];
int n;
bool solve()
{
    if(n&1)//n为奇数
        return false;
    int half = n / 2;
    pair<int, int > cen;//center * 2(为了避免精度问题)
    cen.first = a[1].first + a[1+half].first;
    cen.second = a[1].second + a[1+half].second;
    for(int i = 2; i <= half;i++){
        if(a[i].first + a[i+half].first != cen.first ||
        a[i].second + a[i+half].second != cen.second)
        {
            return 0;
        }
    }
    return 1;
}
int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d%d", &a[i].first, &a[i].second);
    }
    if(solve()) puts("YES");
    else puts("NO");
    return 0;
}

E

​

InputCopy

5
I want to order pizza

OutputCopy

Iwantorderpizza

InputCopy

5
sample please ease in out

OutputCopy

sampleaseinout

题解

这一道题目是可以使用哈希进行计算的，只不过是但是看错了题目，以为是一个单词以及一个单词之间进行考虑，但是实际上是前面所有的已经拼接好的单词与之后的单词进行取最长的前缀已经最长的后缀。

Amugae will merge his sentence left to right (i.e. first merge the first two
words, then merge the result with the third word and so on)

细细地品读：把合并之后的结果再与剩下的单词进行合并！

如果使用哈希来进行求解，一直卡在65处 哈希太折磨人了，所以我先浅浅学习KMP的写法

注意：其实对于这一道题目，简简单单的KMP就可以做，这是因为KMP的时候取的两个字符串的最小长度。

代码

#include 
#include 
using namespace std;
#define N 1000300
int n;
char f[N];
char w[N];
int flen, wlen;
char tmp[N];
int nxt[N];
int tlen;
vector<char> ans;
void KMP()
{
    nxt[0] = 0;
    for(int i = 1; i < tlen; i++)
    {
        int j = nxt[i-1];
        while(j >= tlen/2) j = nxt[j-1];//注意：必须要加这一个条件，否则对于一下样例会寄
/*
5
1101 1001 001001 101 010
Output
110100100101
Answer
1101001001010
*/
        while(j > 0 && tmp[j] != tmp[i]) j = nxt[j-1];
        if(tmp[j] == tmp[i]) j++;
        nxt[i] = j;
    }

}

int main()
{
    scanf("%d", &n);
    scanf("%s", f+1);
    flen = strlen(f+1);
    for(int i = 1; i <= flen; i++) ans.push_back(f[i]);
    for(int T = 1; T <= n-1; T++)
    {
        scanf("%s", w+1);
        wlen = strlen(w+1);
        int t = min(wlen, flen);
        tlen = 0;
        for(int i = 1; i <= t; i++) tmp[tlen++] = w[i];
        for(int i = flen - t + 1; i <= flen; i++) tmp[tlen++] = f[i];//改动
        KMP();
        // for(int i = 0; i < tlen; i++) putchar(tmp[i]);
        // printf("  %d", nxt[tlen-1]);
        // puts("");
        int k = min(t, nxt[tlen-1]);
        for(int i = k+1; i <= wlen; i++) f[++flen] = w[i];
    }
    for(int i = 1; i <= flen; i++) putchar(f[i]);
    return 0;   
}

G

​

tCopy

6 3
1 3 9 8 24 1

OutputCopy

5

题解

一般情况，遇到乘积的情况，可以考虑进行质因数分解。

对于一个任意的整数x，一定可以进行质因数分解。得到$p_0^{r_0}{p}_1^{r_1}{p}_2^{r_2}...$由于要求两个数字的乘积是$x^k$，所以所选中的两个数字相乘之后所得到的质因数分解后的每一个质因数的幂必须是K的整数项。当且仅当这种情况，才可以构造一个数字x

对此我们可以把所给的表的质因数分解，并且存储到vector中vector<质因数, 次幂%k>

为什么要进行取模？
这是因为对于两个数字相加的结果是K的倍数，当且仅当他们对k取余的值相加，然后对k取模的值为0

同时利用STL中的map，可以存储当前情况下的互补对
意思是在a[i]中当前遍历的数字分解后为vector<质因数, 次幂%k>，他的互补对为vector<质因数, (k+k-次幂%k)%k>.当然需要注意，当 次幂%k 已经是0的时候就不需要进行存储（以空缺表示0）
否则，{pair<2, 0>， pair<3, 1>}与{pair<3, 1>}会被视为不同的情况。

时间复杂度

由于$a_i<10^5$，所以分解的质因数的个数最多有十几个（$lo{g}_{2}10^5$）,所以时间复杂度应该是nlogn

代码

#include 
#include 
using namespace std;
typedef long long ll;
#define N 100020
map<vector<pair<int, int> >, int> aim;//与当前互补的个数
vector<pair<int, int> > tmp;
int a[N];
int n, k;
inline void divide(int u)//分解质因数板子题
{
    int x = u;
    for(int i = 2; i <= x / i; i++)//i <= u / i放置爆炸
    {
        int num = 0;
        while(x % i == 0){
            num++;
            x /= i;
        }
        num %= k;
        if(num) tmp.push_back({i, num%k});
    }
    if(x> 1) tmp.push_back({x, 1});
}
int main()
{
    ll ans = 0;
    scanf("%d%d", &n, &k);
    for(int i = 1; i <= n; i++) scanf("%d", a+i);
    for(int i = 1; i <= n; i++)
    {
        tmp.clear();
        divide(a[i]);
        ans += aim[tmp];
        for(auto &x: tmp){
            x.second = (k + k - x.second) % k;
        }
        aim[tmp]++;
    }
    cout << ans;
}

I

​

题解

我们考虑无法越过的情况：

$$\frac{a}{n}=\frac{b}{m}$$

其中，n，m与题目中的相同，a表示里面的第a块顺时针边界上的坐标（一个圆的坐标是1），b表示里面的第b块顺时针边界上的坐标。

进行移项，有：

$$a=\frac{b\times n}{m}$$

$$a=\frac{b\times p}{q}(把m以及n进行约分)$$

容易知道，只有外面的墙以及里面的墙重合的时候，才会挡住去路。

由下面的式子，只有a是p的倍数的时候，会挡住去路。

所以可以把内部的圆分为$\frac{n}{p}$份。每一份中是相互可达的。

对于在外面的情况，可以转化到与其可达的内部进行计算。

代码

    #include 
    using namespace std;
    typedef long long ll;
    pair<ll, ll> a, b;
    int main()
    {
        ll n, m, q;
        cin >> n >> m >> q;
        ll gcd = __gcd(n, m);
        n /= gcd;
        m /= gcd;
        while(q--)
        {
            scanf("%lld%lld%lld%lld", &a.first, &a.second, &b.first, &b.second);
            if(a.first == 2){//对于外面的情况，进行转化！
                a.second = (ll)ceil((long double)a.second*n/m);
            }
            if(b.first == 2){
                b.second = (ll)ceil((long double)b.second*n/m);
            }
            //cout << a.second << b.second;
            if((a.second-1)/n == (b.second-1)/n){
                puts("YES");
            }
            else{
                puts("NO");
            }
        }
        //system("pause");
        return 0;
    }

K

​

题解

(This is a 水题，用时10min)

这一道题目采用贪心来进行求解。

贪心的状态就是我的包包里面所放置的砖头越多越好（多了没有任何坏处）

证明：

对于今后的某一个状态：

1. 如果当前列高于后面的列（差大于k），那么我就可以把砖头塞到包包里面。
2. 如果要是低于后面的列（差大于K），那么我就需要把包包里面的石头往外面掏。

对于第一种，不构成问题，但是对于第二种，如果包包里面没有那么多石头，那么就寄。

所以我每时每刻应该在当前位置可以转移到下一个位置的情况下（t = max(a[i+1]-k, 0);），尽可能的把当前列的桩头拿起来。

代码

#include 
#include 
using namespace std;
#define N 200
int a[N];
int n, m, k;
bool solve()
{
    for(int i = 1; i < n; i++)
    {
        int t = max(a[i+1]-k, 0);
        if(a[i] >= t){
            m += a[i] - t;
        }
        else {
            m -= a[i+1] - k - a[i];
            if(m < 0) return false;
        }
    }
    return true;
}
int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        scanf("%d%d%d", &n, &m, &k);
        for(int i = 1; i <= n; i++) scanf("%d", a+i);
        if(solve()) puts("YES");
        else puts("NO");
    }

    return 0;
}