UHPC的疲劳计算——兼论ModelCode2010的适用性

0. 背景

今年年初，有一位用UHPC做混凝土塔筒的同行告诉我，UHPC的疲劳不能用ModelCode的方法计算（感兴趣的可以点击这里），原因是UHPC的本构与一般混凝土的不一样，从而SN曲线也会不一样。

然而，我却找到了一篇文章（当时怎么找的我也记不清楚了，只是最近（202307）读的时候发现有料可爆！！！对原文感兴趣的可以直接下载绑定资源），里面详细的介绍了ModelCode2010 是如何把UHPC的疲劳考虑进去，以及如何与ModelCode1990的疲劳计算方法进行兼容。这样，那位同行的观点就需要修改了。

本文主要是对这篇文章的描述和解释，可以算做是一篇阅读笔记吧！

下面的截图来自Concrete structures for wind turbines这本书，也就是参考文献[4] 中3.6.3节P105。

1、结论及概述

1. Model Code 2010在疲劳的计算上覆盖了常规混凝土（NC），高强混凝土（HPC），超高性能混凝土（UHPC）；
2. 疲劳强度的设计值针对UHPC做了修正，对于NC和HPC会有提高，但是是合理的。

2、MC10对于SN曲线的调整（囊括NC、HPC、UHPC）

2.1 疲劳失效曲面的构建

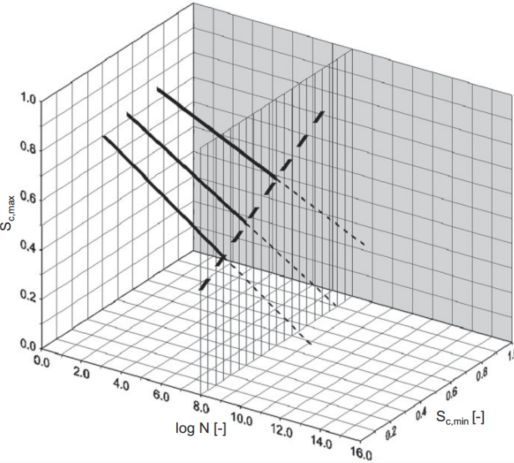
首先，作者将Woehler曲线和Goodman曲线融合在了一起，构建起了包括最大应力、最小应力以及许用循环次数三个变量的疲劳失效曲面（failure surface），如图1所示。

这里体现出了一直在提到的一个观点，即混凝土的疲劳不仅和疲劳荷载的幅值有关系，还与荷载水平本身有着密切的关系。这一点与钢材大不相同。

图1 混凝土失效的模型

在图1中粗实线代表着最小应力确定以后的SN曲线(Woehler 图)，粗虚线代表着给定循环次数以后的应力限制情况（Goodman图）。通过维度拓展实现了对混凝土疲劳的描述。

通过假定对于任何最小应力水平$S_{c,min,i}=const$都有：

1. 在$logN=0$到$logN=8$之间，SN曲线为下降直线，大于$logN=8$时为下降指数型曲线
2. $logN=0$对应$S_{c,max}=1$，即当应力达到设计抗压强度时，只需一次即可压坏。这一点符合常识。

另一方面，假定了在$logN=8$时，选择此时表征应力水平关系的Goodman图的变量关系为一个有理分式(至于为什么要这么选以及相关的系数是怎么解出来的，文章中没有多说，我现在也不是很想做过深的追究。先这样吧~）：
$$S_{c,max}=\frac{a+b\cdot S_{c,min}}{1+c\cdot S_{c,min}+d\cdot S_{c,min}^2}\text{\hspace{1em}(1)}$$
通过选择四个已知点（即原文中$P_{1,fat}$、$P_{2,fat}$、$P_{3,fat}$、$P_{4,fat}$）的疲劳实验数据，然后反解出来式(1)中的4个参数$a$、$b$、$c$、$d$。

至此，整个疲劳失效曲面的构建已经完成。

2.2 新模型的验证

基于2.1给出的疲劳失效曲面模型，原文又给出了一共272个实验样本，包括了不同的强度等级，不同的加载频率以及UHPC是否加纤维，热养护等等。当然，最小应力水平$S_{c,min}$是给定的，等于0.05。具体可以看下面图2。

图2 新疲劳模型与实验的对比

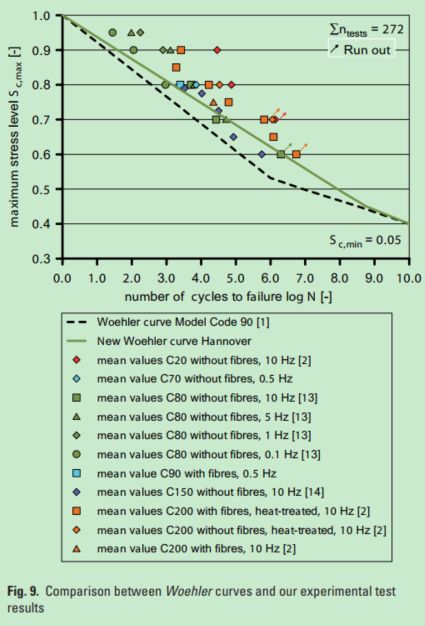
关于上面的验证，有下面两点结论需要格外关注：

1. MC90给出的SN曲线偏于保守
2. 对于HPC和UHPC，添加纤维以后，疲劳性能是下降的（这一点对于风电混塔设计尤为重要！！！）

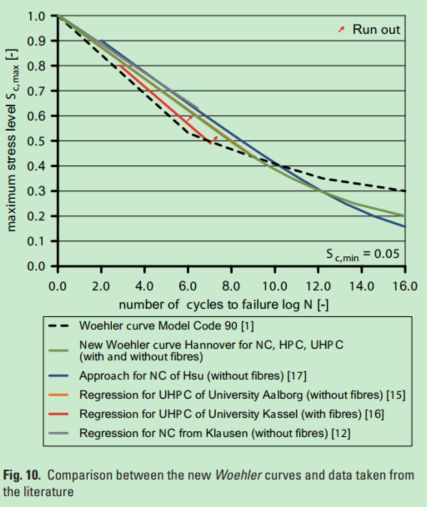
除此之外，原文还对比了过往文献中的数据，大致意思就是不同模型之间差别不是很大。但是：

1. MC90给出的SN曲线偏于保守

具体情况看图3：

图3 不同文献中的SN曲线对比

最后，作者还不太放心的把不同最小应力水平下，MC90和MC10的SN曲线放在了一起对比了一下，就是这样子的：

图4 MC90和MC10的SN曲线对比

可以看出，在循环次数较低的区间里（$logN\le 8$），MC90是保守的；在循环次数较高的区间里（$logN>8$），MC10是比较保守的。

3、MC10对于疲劳设计强度的调整及其背后的原因

前面的讨论都是基于荷载端的处理，本小节关于抗力端的处理方法给出一些说明。这一小节的内容，算是给之前关于ModelCode2010（MC10）正确版本的问题（对原问题感兴趣的可以点击这里）画上一个完美的句号。也算是我挖坟有功了。

在MC10正式版本发布之前（包括正式版的MC90以及最初几版MC10的草稿），关于混凝土的疲劳强度设计值都是长这样的：
$$f_{cd,fat}=0.85\cdot {\beta }_{cc}(t)\cdot \frac{f_{ck}}{{\gamma }_c}\cdot (1-\frac{f_{ck}}{250})\text{\hspace{1em}(2)}$$

上面式子中，因子$(0.85\cdot {\beta }_{cc}(t)\cdot \frac{f_{ck}}{{\gamma }_c})$是混凝土强度设计值$f_{cd}$，因子$(1-\frac{f_{ck}}{250})$是用于疲劳强度的折减系数${\alpha }_{fat}$。

在MC90的时代，强度等级最高的混凝土$f_{ck}=120Mpa$，其疲劳强度折减了将近一半（$(1-\frac{120}{250})=0.52$）。而在MC10的时代，UHPC应用越来越广泛，这意味着当$f_{ck}>120Mpa$的情况下，其疲劳强度设计值折减过半。甚至面临强度等级越高，疲劳设计强度越低的情况，这显然和实际情况不太相符。图5中黑色虚线给出了MC90的情况，可以看出在$f_{ck}>120Mpa$的情况下，其取值变得不再合理。

图5 不同情况下强度特征值与疲劳强度设计值的对比

基于上面提到的情况，原文给出了一个修正如下：

$$f_{cd,fat}=0.85\cdot {\beta }_{cc}(t)\cdot \frac{f_{ck}}{{\gamma }_c}\cdot (1-\frac{f_{ck}}{400})\text{\hspace{1em}(3)}$$

修正的总体思路就是，MC10的混凝土强度等级覆盖到了$f_{ck}=200Mpa$的范围，那么就让$f_{ck}=200Mpa$时疲劳强度折减系数${\alpha }_{fat}=0.52$。基于这一点，给出了式（3）。当然，文中还考虑了其他的因素，诸如安全可靠性，经济适用性等等。但主要做法就是基于上面的操作。

4. 结语

行文至此，基本把MC10中疲劳的计算方法来源捋了一遍。也搞清楚了为何当初我们大家手里拿着不同版本的ModelCode，同样强度等级的混凝土算出的疲劳结果有那么大的差异。当然，最重要的还是搞清楚了MC10的疲劳计算是适用于UHPC的。

同时也很感慨，老外做事真的很值得我们学习！他们把每一步掰开揉碎了讲的清清楚楚明明白白，是什么就是什么，绝对不会装神弄鬼。

最后，再拜！