字节跳动2022.3.13笔试

题目1

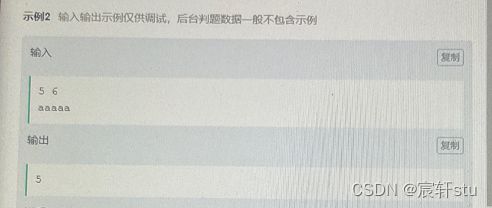
1、题目描述

2、算法分析

gg，题目没读懂！

------------------------------------------------------------------------------------------------------------------

题目2：

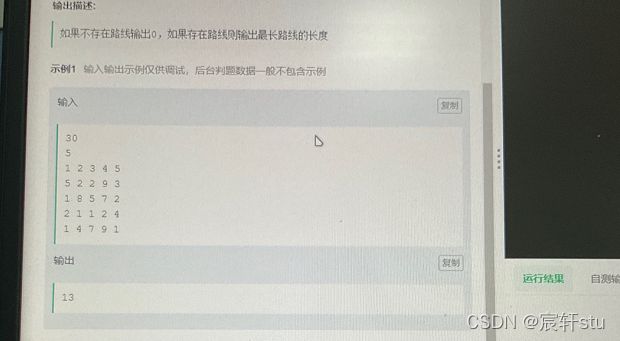
1、题目描述

 

 2、算法分析

首先根据题意，从当前点到下一个目标点的时候，首先是先跳一步，然后如果没有到达target位置，那么后续跳的距离是前一次距离长度+1；

然后，还有一个点 是 我们要向左 还是向右跳，什么时候向左，什么时候向右；

我的想法是：

当前 位置 a,  步长 step ，终点b
if(a + step == b)  return
if(a + step < b)  a = a + step   step ++;
if(a + step > b) a = a -step step ++;

3、代码

import java.io.*;
import java.util.*;
class Test{
    
    public static void main(String[] args)
    {
        Scanner sc = new Scanner(System.in);
        int n =sc.nextInt();
        int[] arr = new int[n];
        for(int i=0;i

But，好像不能通过所有额的测试用例，发现在力扣有原题：

传送门：力扣

------------------------------------------------------------------------

题目3

1、题目描述

2、算法分析

根据题意我们可以得出以下几点：

1）出口在房间的外圈（x=0|| y==0 || x=rooms.length-1 || y = rooms.length-1）,且同时还有满足到出口刚好把预算的钱用完；

2）走过的地方就不能交叉，因此我们需要一个标记数组来给我们走过的房间一个记号，走过了就不要再走；

3）根据题意可能会出现 多中走法 满足条件1，我们要输出在rooms里面走了步数最多的那条走法的步数

===》像这种路径试探，找组合的，找到一种可能还需要找其他可能，存在回退操作的，联想到了回溯算法。

3、代码

import java.io.*;
import java.util.*;
class Test{
    //回溯
    public static void main(String[] args)
    {
        Scanner sc = new Scanner(System.in);
        int money =sc.nextInt();//预算
        int n =sc.nextInt();//房间个数
        int[][] rooms = new int[n][n];//房间里面存储的成本
        for(int i=0;i=rooms.length||y<0||y>=rooms.length||isUsed[x][y]){
            return 0;
        }
        //预算没了
        if(money-rooms[x][y]<0){
            return 0;
        }
        //收割结果,钱用完了，同时刚好到达了房间外圈的边界
        if(money-rooms[x][y]==0 && (x==0 ||y==0||x==rooms.length-1||y==rooms.length-1)){
            return size+1;
            
        }
        
        //回溯主体
        int max=0; //维护可能存在走法中，在房间中走了房间网格最多的那条走法的步数
        isUsed[x][y]=true;
        max = Math.max(max, backtrack(rooms, isUsed, new int[]{x+1,y}, size+1, money-rooms[x][y]));//向下
        max = Math.max(max, backtrack(rooms, isUsed, new int[]{x,y+1}, size+1, money-rooms[x][y]));//向右
        max = Math.max(max, backtrack(rooms, isUsed, new int[]{x-1,y}, size+1, money-rooms[x][y]));//向上
        max = Math.max(max, backtrack(rooms, isUsed, new int[]{x,y-1}, size+1, money-rooms[x][y]));//向左
        
        isUsed[x][y]=false;//撤销节点
        return max;
        
    }
   
}

-----------------------------------------------------------------------------------------------------

题目4

1、题目描述