【Golang系统开发】搜索引擎(1) 如何快速判断网页是否已经被爬取
文章目录
- 1. 写在前面
- 2. 数组存储
- 3. 位图存储
-
- 3.1 位图简介
- 3.2 链表法
- 3.3 开放寻址法
1. 写在前面
在实际工作中,我们经常需要判断一个对象是否存在,比如判断用户注册登陆时候,需要判断用户是否存在,再比如搜索引擎中的爬虫,判断该网页是否已经爬过,减少一些重复的工作。
2. 数组存储
我们当然可以使用有序数组,二叉搜索树,哈希表等等来存储所有的用户id。但是无论是有序数组还是二叉搜索树,这两种数据结构都是基于二分查找的思想从中间元素开始查起的。所以在查询用户id是否存在时,这两种数据结构的检索时间都是 O(logn)。
而哈希表的检索时间是O(1)。因此如果我们希望能快速查询元素是否存在,那哈希表就是最合适的。但是哈希表中,我们还是需要计算哈希值来获取数组的下标,这也是需要耗费一定的时间。
那应该怎么做呢?
我们可以直接使用一个足够大的数组来存储用户id,如果该用户存在,就在该用户id的位置标识为 1 ,否则就是默认的 0 也就是不存在。但是这个也会有问题,如果我们的用户id范围很广,比如说是在10w之内,那我们就需要保证数组的长度是大于10w的,除此之外,如果这个数组是int类型的话,每个元素就会占据4/8个字节,用4/8个字节存储0和1是不是很浪费空间,所以这个方案比较消耗空间,典型的空间换时间。
那么我们怎么优化存储空间呢?接下来就介绍一下位图了。
3. 位图存储
3.1 位图简介
首先我们需要优化存储的数据结构,不是int,虽然char和bool类型都是1字节,相比较于4/8字节的int类型,已经提升了4/8倍了(32位的机器是4 byte,64位的机器是8 byte),但是其实用字节作为单位来存储一个flag类型也是很浪费的,flag类型的直接使用bit类型的就可以了。
如果我们使用bit类型来存储,就是原来的32倍了,非常亏贼!而这种以bit为单位构建数组的方案就叫做bitmap,也就是位图。
如果你在好奇这个32是怎么算的?我们原来是用一个int类型取表示是否存在这个值,我们假设是在32位的机子上,这个int类型就是4个byte。而我们现在用的是bit来作为存储运算,1 byte = 8 bit,所以就是原来的 1/4*8 ,就是1/32倍。
虽然位图相对于原始数组来说,在元素存储上已经有了很大的优化,但如果我们还想进一步优化存储空间,要怎么做呢?
其实有一个点很好想到,我们都知道一个数组的空间其实就是 数组元素的个数 * 每个元素大小,位图已经把我们每个元素的大小限定在最小单位的bit了,而我们存储元素的个数一定要大于我们所需要存储的用户id数的,这似乎已经无解了。但其实我们可以通过哈希算法将大于数组长度的用户id转化成一个小于数组长度的数值作为下标,除此之外, 使用哈希函数还可以使我们的用户id不需要是正整数,可以是字符串,因为字符串可以通过哈希函数的转换成正整数。
当然如果我们数组压缩到很小的时候,就容易发生哈希冲突,如果两个元素,A和B都映射到同一个地方了,那么就无法判断是A存在,还是B存在了,那应该如何解决哈希冲突呢?一般会有两种方法,开放寻址法,链表法
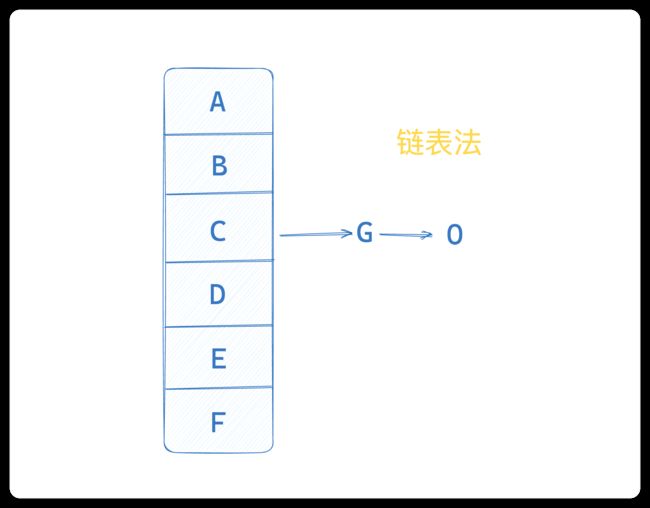
3.2 链表法
数组的每个成员是一个链表。该数据结构所容纳的所有元素均包含一个指针,用于元素间的链接。我们根据元素的自身特征把元素分配到不同的链表中去,也是根据这些特征,找到正确的链表,再从链表中找出这个元素。
先调用这个元素的 hash 方法,然后根据所得到的值计算出元素应该在数组的位置。如果这个位置上没有元素,那么直接将它存储在这个位置上;如果这个位置上已经有元素了,那么与新元素进行比较:相同的话就不存了,否则,将其存在这个位置对应的链表中。
3.3 开放寻址法
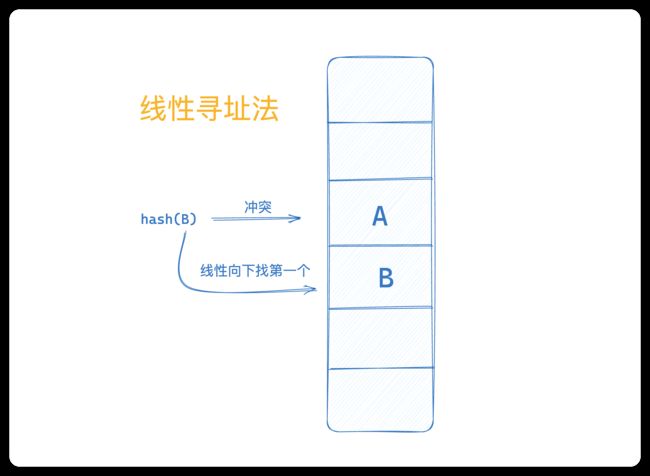
当发生哈希冲突时,重新找到空闲的位置,然后插入元素。寻址方式有多种,常用的有线性寻址、二次方寻址、双重哈希寻址等等
线性寻址就是如果冲突了,就从冲突位置线性顺序向下继续寻找空位置。
二次寻址就是每次向上找两格,冲突就向下找两格,再冲突就是向上找四个,-2,+2,-4,+4这样的上下的找,直到找到不冲突为止。
双重哈希寻址就是使用多个hash函数获取多个哈希值。 而这种方法也称为双散列。可以使用两个哈希寻址,也可以使用多个哈希来寻址,那这是不是就有点像布隆过滤器。在布隆过滤器中,如果我们对一个对象,使用来N个哈希函数,就会得到N个值,也就是N个下标,我们会把数组中对应下标位置都变成1。
而布隆过滤器和位图最大的区别就是我们不再使用一位来表示一个对象,而是使用N位来表示一个对象。这样两个对象的N位都相同的概率就会大大降低了,就能大大缓解哈希冲突了。
而N个哈希都冲突的情况也是会有的,或者说刚好是下面这种Z的情况
那么我们就当这个Z是已经存在了,让用户重新输入就好了,因为在大多数系统中,我们并不要求100%的准确,我们只要保证用户体验就行了,这种方案已经是权衡很多之后才确定是最优解了。
这个X,Y,Z其实就是我们的网址。这样我们就可以快速判断网页是否已经被爬取了。
还有一种位图的优化:Roaring Bitmap 后续在合并多个postingsList会有作用。