动手学深度学习-pytorch版本（一）：引言 & 预备知识

参考引用

• 动手学深度学习
• 利用 Anaconda 安装 pytorch 和 paddle 深度学习环境 + pycharm 安装

0. 环境安装

• 利用 Anaconda 安装 pytorch 和 paddle 深度学习环境 + pycharm 安装

1. 引言

• 机器学习（machine learning，ML）是⼀类强⼤的可以从经验中学习的技术。通常采⽤观测数据或与环境交互的形式，机器学习算法会积累更多的经验，其性能也会逐步提⾼

1.1 日常生活中的机器学习

• 假如需要编写程序来响应⼀个 “唤醒词”，比如 “Alexa”

  • 收集⼀个包含⼤量音频样本的数据集 (dataset)，并对包含和不包含唤醒词的样本进⾏标记
  • 利用机器学习算法，不需要设计⼀个 “明确地” 识别唤醒词的系统，只需要定义⼀个灵活的程序算法，其输出由许多参数 (parameter) 决定，然后使用数据集来确定当下的 “最佳参数集”，这些参数通过某种性能度量方式来达到完成任务的最佳性能
  • 什么是参数?
    • 任一调整参数后的程序被称为模型 (model)。通过操作参数而生成的所有不同程序（输入-输出映射）的集合称为 “模型族”。使用数据集来选择参数的元程序被称为学习算法
  • 必须精确地定义问题，确定输入 (input) 和输出 (output) 的性质，并选择合适的模型族。在本例中，模型接收一段音频作为输入，然后在是或否中生成一个选择作为输出
    • 如果想处理完全不同的输入或输出，比如：从图像映射到字幕，或从英语映射到中文，可能需要一个完全不同的模型族

• 机器学习中，学习 (learning) 是一个训练模型的过程。通过这个过程，可以发现正确的参数集，从而使模型强制执行所需的行为。换句话说，用数据训练 (train) 模型。训练过程通常包含如下步骤

  • （1）从一个随机初始化参数的模型开始，这个模型基本没有 “智能”
  • （2）获取一些数据样本 (例如，音频片段以及对应的是或否标签)
  • （3）调整参数，使模型在这些样本中表现得更好
  • （4）重复第 (2) 步和第 (3) 步，直到模型在任务中的表现令人满意

1.2 机器学习中的关键组件

1.2.1 数据（data）

• 每个数据集由一个个样本 (sample) 组成，大多时候，它们遵循独立同分布。样本有时也叫做数据点 (data point) 或数据实例 (data instance)，通常每个样本由一组称为特征 (features，或协变量 (covariates)) 的属性组成，机器学习模型会根据这些属性进行预测。假设要预测的是一个特殊的属性，它被称为标签 (label，或目标 (target))

  • 当处理图像数据时，每一张单独的照片即为一个样本，它的特征由每个像素数值的有序列表表示

• 当每个样本的特征类别数量相同时，其特征向量是固定长度的，这个长度被称为数据的维数 (dimensionality)。然而，并不是所有的数据都可以用 “固定长度” 的向量表示，与传统机器学习方法相比，深度学习的一个主要优势是可以处理不同长度的数据

• 更多的数据可以被用来训练出更强大的模型，仅仅拥有海量的数据是不够的，还需要正确的数据。如果数据中充满了错误，或者如果数据的特征不能预测任务目标，那么模型很可能无效

  • 比如在一个有关医疗的训练数据集中，要训练一个皮肤癌识别模型，但在训练数据集中从未 “见过” 黑色皮肤的人群，这个模型就会顿时束手无策
  • 当数据不具有充分代表性，甚至包含了一些社会偏见时，模型就很有可能有偏见

1.2.2 模型（model）

• 大多数机器学习会涉及到数据的转换
  • 比如一个 “摄取照片并预测笑脸” 的系统
  • 再比如通过摄取到的一组传感器读数预测读数的正常与异常程度

  深度学习与经典方法的区别主要在于：前者关注功能强大的模型，这些模型由神经网络错综复杂的交织在一起，包含层层数据转换，因此被称为深度学习 (deep learning)

1.2.3 目标函数（objective function）

• 在机器学习中需要定义模型的优劣程度的度量，这个度量在大多数情况是 “可优化” 的，这被称之为目标函数 (obiective function)。通常定义一个目标函数，并希望优化它到最低点。因为越低越好，所以这些函数有时被称为损失函数 (loss function，或 cost function)

  • 当任务在试图预测数值时，最常见的损失函数是平方误差 (squared error)，即预测值与实际值之差的平方
  • 当试图解决分类问题时，最常见的目标函数是最小化错误率，即预测与实际情况不符的样本比例
  • 有些目标如错误率，由于不可微性或其他复杂性难以直接优化，此时通常会优化替代目标

• 通常，损失函数是根据模型参数定义的，并取决于数据集。在一个数据集上，可以通过最小化总损失来学习模型参数的最佳值

  • 该数据集由一些为训练而收集的样本组成，称为训练数据集 (training dataset，或称为训练集(training set))
  • 然而，在训练数据上表现良好的模型，并不一定在 “新数据集” 上有同样的性能，这里的 “新数据集” 通常称为测试数据集 (test dataset，或称为测试集(test set))

• 可用数据集通常可以分成两部分：训练数据集用于拟合模型参数，测试数据集用于评估拟合的模型

  • “一个模型在训练数据集上的性能” 可以被想象成 “一个学生在模拟考试中的分数”，这个分数用来为一些真正的期末考试做参考，即使成绩令人鼓舞，也不能保证期末考试成功
  • 当一个模型在训练集上表现良好，但不能推广到测试集时，这个模型被称为过拟合 (overftting) 的。就像在现实生活中，尽管模拟考试考得很好，真正的考试不一定百发百中

1.2.4 优化算法（optimization algorithm）

• 当获得了一些数据源及其表示、一个模型和一个合适的损失函数，接下来就需要一种算法，它能够搜索出最佳参数，以最小化损失函数。深度学习中，大多流行的优化算法通常基于一种基本方法：梯度下降 (gradientdescent)
  • 在每个步骤中，梯度下降法都会检查每个参数，观察如果仅对该参数进行少量变动，训练集损失会朝哪个方向移动
  • 然后，它在可以减少损失的方向上优化参数

1.3 各种机器学习问题

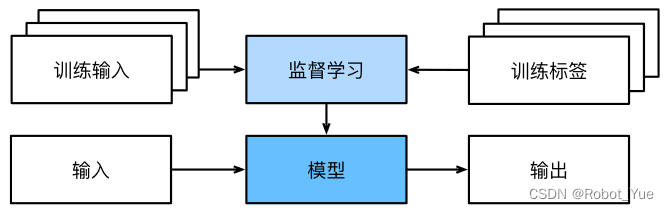
1.3.1 监督学习 (supervised learning)

• 监督学习 (supervised learning) 擅长在 “给定输入特征” 的情况下预测标签。每个 “特征-标签” 对都称为一个样本 (example)。有时即使标签是未知的，样本也可以指代输入特征。目标是生成一个模型，能够将任何输入特征映射到标签 (即预测)

  • 例：假设需要预测患者的心脏病是否会发作，那么观察结果 “心脏病发作” 或 “心脏病没有发作” 将是样本的标签。输入特征可能是生命体征，如心率、舒张压和收缩压等

• 监督学习之所以能发挥作用，是因为在训练参数时为模型提供了一个数据集，其中每个样本都有真实的标签。工业中，大部分机器学习的成功应用都使用了监督学习。这是因为许多重要的任务可描述为：在给定一组特定的可用数据的情况下，估计未知事物的概率。比如:

  • 给出一个英语句子，预测正确的法语翻译
  • 根据本月的财务报告数据，预测下个月股票的价格

• 监督学习的学习过程一般可以分为三大步骤:

  • 1、从已知大量数据样本中随机选取一个子集，为每个样本获取真实标签。有时，这些样本已有标签 (例如患者是否在下一年内康复?)；有时，这些样本可能需要被人工标记 (例如，图像分类)。这些输入和相应的标签一起构成了训练数据集
  • 2、选择有监督的学习算法，它将训练数据集作为输入，并输出一个 “已完成学习的模型”
  • 3、将之前没有见过的样本特征放到这个 “已完成学习的模型” 中，使用模型的输出作为相应标签的预测

1.3.1.1 回归

• 回归 (regression) 是最简单的监督学习任务之一，生活中的许多问题都可归类为回归问题，判断回归问题的一个很好的经验法则是，任何有关 “有多少” 的问题很可能就是回归问题。比如:
  • 这个手术需要多少小时
  • 在未来 6 小时，这个镇会有多少降雨量

1.3.1.2 分类

• 设计一款应用程序能够自动理解从图像中看到的文本，并将手写字符映射到对应的已知字符之上。这种 “哪一个” 的问题叫做分类 (classification) 问题。分类问题希望模型能够预测样本属于哪个类别 (category，类(class))

  • 最简单的分类问题是只有两类，这被称之为二项分类 (binomial classification)；当有两个以上的类别时，把这个问题称为多项分类 (multiclass classification) 问题
  • 回归是训练⼀个回归函数来输出⼀个数值；分类是训练一个分类器来输出预测的类别，与解决回归问题不同，分类问题的常见损失函数被称交叉熵 (cross-entropy)

• 用概率语言来理解模型：给定一个样本特征，模型为每个可能的类分配一个概率。比如，猫狗分类例子中，分类器可能会输出图像是猫的概率为 0.9：分类器 90% 确定图像描绘的是一只猫。预测类别的概率大小传达了一种模型的不确定性

• 分类可能变得比二项分类、多项分类复杂得多。例如，有一些分类任务的变体可以用于寻找层次结构，层次结构假定在许多类之间存在某种关系。因此，并不是所有的错误都是均等的。人们宁愿错误地分入一个相关的类别，也不愿错误地分入一个遥远的类别，这通常被称为层次分类 (hierarchical classifcation)

1.3.1.3 标记问题

• 学习预测不相互排斥的类别的问题称为多标签分类 (multi-label classifcation)。举个例子，人们在技术博客上贴的标签：“机器学习” “技术” “小工具” “编程语言” “Linux” “云计算” “AWS”。一篇典型的文章可能会用 5~10 个标签，因为这些概念是相互关联的。关于 “云计算” 的帖子可能会提到 “AWS”，而关于 “机器学习” 的帖子也可能涉及 “编程语言”

1.3.2 无监督学习 (unsupervised learning)

• 以上所有的例子都与监督学习有关，即需要向模型提供巨大数据集：每个样本包含特征和相应标签值。如果工作没有十分具体的目标，就需要 “自发” 地去学习了。比如，老板可能会给我们一大堆数据，然后要求用它做一些数据科学研究，却没有对结果有要求。这类数据中不含有 “目标” 的机器学习问题通常称为无监督学习
  • 聚类 (clustering)
    • 没有标签的情况下是否能给数据分类呢? 比如，给定一组照片，能把它们分成风景照片、狗、婴儿、猫和山峰的照片吗? 同样，给定一组用户的网页浏览记录，能否将具有相似行为的用户聚类呢?
  • 主成分分析 (principal component analysis):
    • 能否找到少量的参数来准确地捕捉数据的线性相关属性？比如，一个球的运动轨迹可以用球的速度、直径和质量来描述。再比如，裁缝们已经开发出了一小部分参数，这些参数相当准确地描述了人体的形状，以适应衣服的需要
  • 因果关系 (causality) 和概率图模型 (probabilistic graphical models)
    • 能否描述观察到的许多数据的根本原因? 例如，如果有关于房价、污染、犯罪、地理位置、教育和工资的人口统计数据，能否简单地根据经验数据发现它们之间的关系?

1.3.3 强化学习 (reinforcement learning)

• 不管是监督学习还是无监督学习，都会预先获取大量数据，然后启动模型，不再与环境交互。这里所有学习都是在算法与环境断开后进行的，被称为离线学习 (offline learning)

• 强化学习不需要输入数据集，并能与环境交互且采取行动。这可能包括应用到机器人、对话系统，甚至开发视频游戏的人工智能。深度强化学习(deep reinforcement learning) 将深度学习应用于强化学习的问题

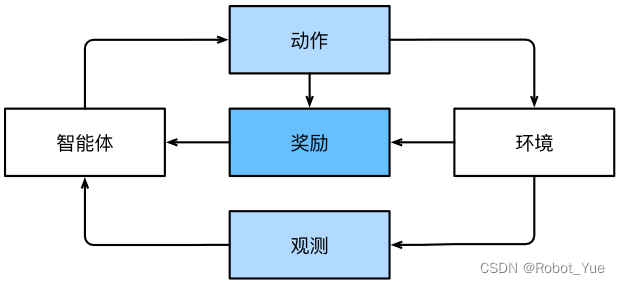
• 在强化学习问题中，智能体 (agent) 在一系列的时间步骤上与环境交互。在每个特定时间点，智能体从环境接收一些观察 (observation)，并且必须选择一个动作 (action)，然后通过某种机制 (有时称为执行器) 将其传输回环境，最后智能体从环境中获得奖励 (reward)。此后新一轮循环开始，智能体接收后续观察，并选择后续操作，依此类推

强化学习的目标是产生一个好的策略 (policy)。强化学习智能体选择的 “动作” 受策略控制，即一个从环境观察映射到行动的功能

1.4 深度学习的起源

• 为了解决各种各样的机器学习问题，深度学习提供了强大的工具。虽然许多深度学习方法都是最近才有重大突破，但使用数据和神经网络编程的核心思想已经研究了几个世纪

• 神经网络 (neural networks) 的得名源于生物灵感。研究人员一直试图组装类似于相互作用的神经元网络的计算电路，其核心是当今大多数网络中都可以找到的几个关键原则:

  • 线性和非线性处理单元的交替，通常称为层 (layers)
  • 使用链式规则 (也称为反向传播 (backpropagation)) 一次性调整网络中的全部参数

1.5 深度学习的发展

• 新的容量控制方法：如 dropout(Srivastava et al,2014)，有助于减轻过拟合的危险
• 注意力机制：如何在不增加可学习参数的情况下增加系统的记忆和复杂性
• 多阶段设计：例如，存储器网络 (Sukhbaatar et al,2015) 和神经编程器-解释器 (Reed and De Freitas.2015)
• 生成对抗网络 ：(Godfellow et al,2014)。生成式对抗性网络的关键创新是：用具有可微参数的任意算法代替采样器。然后对这些数据进行调整，使得鉴别器(实际上是一个双样本测试) 不能区分假数据和真实数据
• 构建并行和分布式训练算法：在许多情况下，单个 GPU 不足以处理可用于训练的大量数据
• 深度学习框架：在传播思想方面发挥了至关重要的作用
  • 第一代框架：Caffe、Torch 和 Theano
  • 第二代框架：TensorFlow、CNTK、Caffe2 和 Apache MXNet
  • 第三代框架：PyTorch、MXNet 的 Gluon API 和 Jax

1.6 深度学习的特点

• 机器学习是人工智能的一个分支/方法，而深度学习是机器学习的一个子集

• 机器学习可以使用数据来学习输入和输出之间的转换，例如在语音识别中将音频转换为文本。在这样做时，通常需要以适合算法的方式表示数据，以便将这种表示转换为输出

  • 深度学习是 “深度” 的，模型学习了许多 “层” 的转换，每一层提供一个层次的表示
  • 例如，靠近输入的层可以表示数据的低级细节，而接近分类输出的层可以表示用于区分的更抽象的概念
  • 由于表示学习 (representation learning) 目的是寻找表示本身，因此深度学习可以称为 “多级表示学习”

• 深度学习方法中最显著的共同点是使用端到端训练：与其基于单独调整的组件组装系统，不如构建系统，然后联合调整它们的性能。因此，深度学习的一个关键优势：不仅取代了传统学习管道末端的浅层模型，还取代了劳动密集型的特征工程过程

2. 预备知识

2.1 数据操作

• n 维数组，也称为张量（tensor），无论使用哪个深度学习框架，它的张量类 (在 MXNet 中为 ndarray，在 Pytorch 和 TensorFlow 中为 Tensor) 都与 Numpy 的 ndarray 类似
  • 深度学习框架比 NumPy 的 ndarray 多一些功能：首先，GPU 很好地支持加速计算，而 NumPy 仅支持 CPU 计算；其次，张量类支持自动微分。这些功能使得张量类更适合深度学习（如果没有特殊说明，本文中所说的张量均指的是张量类的实例）

2.1.1 入门

• 张量表示一个由数值组成的数组，这个数组可能有多个维度。具有一个轴的张量对应数学上的向量 (vector)，具有两个轴的张量对应数学上的矩阵 (atrix)，具有两个轴以上的张量没有特殊的数学名称

  import torch
  
  x = torch.arange(12) # 使用 arange 创建一个行向量，包含以 0 开始的前 12 个整数
  print(x)
  print(x.shape) # 通过张量的 shape 属性来访问张量 (沿每个轴的长度) 的形状
  
  # 如果只想知道张量中元素的总数，即形状的所有元素乘积，可以检查它的大小 (size)
  # 因为这里在处理的是一个向量，所以 shape 与 size 相同
  print(x.numel())
  
  # 要想改变一个张量的形状而不改变元素数量和元素值，可以调用 reshape 函数
  # 虽然张量的形状发生了改变，但其元素值并没有变。通过改变张量的形状张量的大小不会改变
  X = x.reshape(3, 4) # 把张量 x 从形状为 (12,) 行向量转换为形状为 (3, 4) 矩阵
  # 可以通过 -1 来⾃动计算出维度的功能
  # 用 x.reshape(-1,4) 或 x.reshape(3,-1) 来取代 x.reshape(3,4)
  print(X)
  
  # 创建全 0 或全 1 常量
  y = torch.zeros((2, 3, 4))
  y = torch.ones((2, 3, 4))
  print(y)
  
  # 每个元素都从均值为 0、标准差为 1 的标准高斯分布 (正态分布) 中随机采样
  z = torch.randn(3, 4)
  print(z)
  
  # 提供包含数值的 Python 列表 (或嵌套列表)，为所需张量中的每个元素赋予确定值
  # 最外层的列表对应于轴 0，内层的列表对应于轴 1
  w = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
  print(w)
  

2.1.2 运算符

• 对于任意具有相同形状的张量，常见的标准算术运算符 (+、-、*、/ 和 ) 都可以被升级为按元素运算**
• 把多个张量连结 (concatenate) 在一起，把它们端对端叠起来形成一个更大的张量，只需提供张量列表，并给出沿哪个轴连结

  import torch
  
  x = torch.tensor([1.0, 2, 4, 8])
  y = torch.tensor([2, 2, 2, 2, ])
  print(x + y, x - y, x * y, x / y, x ** y) # ** 运算符是求幂运算
  print(torch.exp(x))
  
  x = torch.arange(12, dtype=torch.float32).reshape(3, 4) # 创建一个形状为 (3,4) 的张量 x，其中包含了从 0 到 11 的连续数字，其数据类型为 torch.float32
  y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
  print(torch.cat((x, y), dim=0)) # 将张量x和y在维度0上进行拼接，即将y拼接在x的下方，拼接后的张量形状为(6,4)
  print(torch.cat((x, y), dim=1)) # 将张量x和y在维度1上进行拼接，即将y拼接在x的右侧，拼接后的张量形状为(3,8)
  # 通过逻辑运算符构建二元张量
  # 如果 x 和 y 在该位置相等，则新张量中相应项的值为 1，否则该位置为 0
  print(x == y)
  # 对张量中的所有元素进⾏求和，会产⽣⼀个单元素张量
  print(x.sum())
  

2.1.3 广播机制

• 即使形状不同，仍然可以通过调用广播机制 (broadcasting mechanism) 来执行按元素操作，工作方式如下
  • 通过适当复制元素来扩展一个或两个数组，以便在转换之后，两个张量具有相同的形状
  • 对生成的数组执行按元素操作

import torch

a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
print(a)
print(b)

# 将两个矩阵⼴播为⼀个更⼤的 3×2 矩阵：矩阵 a 复制列，矩阵 b 复制⾏，然后再按元素相加
print(a + b)

2.1.4 索引和切片

• 和 Python 数组一样，张量中的元素可以通过索引访问: 第一个元素的索引是 0，最后一个元素索引是 -1; 可以指定范围以包含第一个元素和最后一个之前的元素

  import torch
  
  x = torch.arange(12, dtype=torch.float32).reshape(3, 4)
  
  
  print(x[-1]) # 用 [-1] 选择最后一个元素
  print(x[1:3]) # 用 [1:3] 选择第二个和第三个元素
  
  # 指定索引来将元素写入矩阵
  x[1, 2] = 9
  print(x)
  
  # 为多个元素赋值相同的值：只需索引所有元素，然后为它们赋值
  x[0:2, :] = 12 # : 表示沿轴 1（列）的所有元素
  print(x)
  

2.1.5 节省内存

• 运行一些操作可能会导致为新结果分配内存。例如，如果用 y = x + y，将取消引用 y 指向的张量，而是指向新分配的内存处的张量

  import torch
  
  x = torch.arange(12, dtype=torch.float32).reshape(3, 4)
  y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
  
  # 使用切片表示法将操作的结果分配给先前分配的数组，例如 Y[:]= 
  z = torch.zeros_like(y) # 使用 zeros_like 来分配一个全 0 的块
  print('id(z):', id(z))
  z[:] = x + y
  print('id(z):', id(z))
  

2.1.6 转换为其他 python 对象

• 将深度学习框架定义的张量转换为 NumPy 张量 (ndarray) 很容易，反之也同样。torch 张量和 numpy 数组将共享它们的底层内存，就地操作更改一个张量也会同时更改另一个张量

  import torch
  
  x = torch.arange(12, dtype=torch.float32).reshape(3, 4)
  A = x.numpy()
  B = torch.tensor(A)
  
  print(type(A), type(B))
  

• 要将大小为 1 的张量转换为 Python 标量，可以调用 item 函数或 Python 的内置函数

  import torch
  
  a = torch.tensor([3.5])
  
  print((a, a.item(), float(a), int(a)))
  

2.2 数据预处理

• 在 Python 中常用的数据分析工具中，通常使用 pandas 软件包，可以与张量兼容

2.2.1 读取数据集

• 首先创建一个人工数据集，并存储在 CSV (逗号分隔值) 文件 …/data/house_tiny.csv中。以其他格式存储的数据也可以通过类似的方式进行处理。下面将数据集按行写入 CSV 文件中
• 要从创建的 CSV 文件中加载原始数据集，导入 pandas 包并调用 read_csv 函数。该数据集有四行三列。其中每行描述了房间数量 (“NumRooms”)、巷子类型 (“Alley”) 和房屋价格 (“Price”)

  import os
  import pandas as pd
  
  os.makedirs(os.path.join('..', 'data'), exist_ok=True)
  data_file = os.path.join('..', 'data', 'house_tiny.csv')
  with open(data_file, 'w') as f:
      f.write('NumRooms,Alley,Price\n')
      f.write('NA,Pave,127500\n')
      f.write('2,NA,106000\n')
      f.write('4,NA,178100\n')
      f.write('NA,NA,140000\n')
  
  data = pd.read_csv(data_file)
  print(data)
  

  # 输出
     NumRooms Alley   Price
  0       NaN  Pave  127500
  1       2.0   NaN  106000
  2       4.0   NaN  178100
  3       NaN   NaN  140000
  

2.2.2 处理缺失值

• “NaN” 项代表缺失值。为了处理缺失的数据，典型的方法包括插值法和删除法，其中插值法用一个替代值弥补缺失值，而删除法则直接忽略缺失值，这里将考虑插值法
  • 通过位置索引 iloc，将 data 分成 inputs 和 outputs，其中前者为 data 的前两列，而后者为 data 的最后一列。对于 inputs 中缺少的数值，用同一列的均值替换 “NaN” 项

  import os
  import pandas as pd
  
  os.makedirs(os.path.join('..', 'data'), exist_ok=True)
  data_file = os.path.join('..', 'data', 'house_tiny.csv')
  with open(data_file, 'w') as f:
      f.write('NumRooms,Alley,Price\n')
      f.write('NA,Pave,127500\n')
      f.write('2,NA,106000\n')
      f.write('4,NA,178100\n')
      f.write('NA,NA,140000\n')
  
  data = pd.read_csv(data_file)
  # 通过位置索引 iloc，将 data 分成 inputs 和 outputs
  # inputs 为 data 的前两列，outputs 为 data 的最后一列
  inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
  inputs = inputs.fillna(inputs.mean())
  
  print(inputs)
  

  # 输出
     NumRooms Alley
  0       3.0  Pave
  1       2.0   NaN
  2       4.0   NaN
  3       3.0   NaN
  

2.2.3 转换为张量格式

• 上面的 inputs 和 outputs 中的所有条目都是数值类型，它们可以转换为张量格式。当数据采用张量格式后，可以通过张量函数来进一步操作

  import torch
  
  x, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
  print(x, y)
  

2.3 线性代数

2.3.1 标量

• 仅包含一个数值被称为标量（scalar），本文中标量变量由普通小写字母表示，标量由只有⼀个元素的张量表示

  import torch
  
  x = torch.tensor(3.0)
  y = torch.tensor(2.0)
  
  print(x + y, x * y, x / y, x**y)
  

2.3.2 向量

• 向量可视为标量值组成的列表，这些标量值被称为向量的元素或分量，向量通常记为粗体、小写的符号
• 通过一维张量表示向量。一般来说，张量可以具有任意长度，取决于机器的内存限制

  import torch
  
  x = torch.arange(4)
  
  print(x)
  

• 通常默认列向量是向量的默认方向，向量 $\mathbf{x}$ 可写为
  x = [ x 1 x 2 ⋮ x n ] \mathbf{x}=\begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix} x= ​x1​x2​⋮xn​​ ​

长度、维度和形状

• 向量只是一个数字数组，就像每个数组都有一个长度一样，每个向量也是如此。在数学表示法中，如果说一个向量 $\mathbf{x}$ 由 n 个实值标量组成，可以将其表示为 $\mathbf{x}\in {\mathbb{R}}^n$。向量的长度通常称为向量的维度 (dimension)

  import torch
  
  x = torch.arange(4)
  print(len(x)) # 调用 Python 的内置 len() 函数来访问张量的长度
  # 当用张量表示一个向量(只有一个轴) 时，也可通过 .shape 属性访问向量长度
  # 形状（shape）是⼀个元素组，列出了张量沿每个轴的⻓度（维数）
  print(x.shape)
  

  维度（dimension）：向量或轴的维度被用来表示向量或轴的长度，即向量或轴的元素数量。然而，张量的维度用来表示张量具有的轴数。因此，在这个意义上，张量的某个轴的维度就是这个轴的长度

2.3.3 矩阵

• 向量将标量从零阶推广到一阶，矩阵将向量从一阶推广到二阶，通常用粗体、大写字母表示，在代码中表示为具有两个轴的张量
• 当矩阵具有相同数量的行和列时，其形状将变为正方形，称为方阵

A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] \mathbf{A}=\begin{bmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{m1}&a_{m2}&\cdots&a_{mn}\end{bmatrix} A= ​a11​a21​⋮am1​​a12​a22​⋮am2​​⋯⋯⋱⋯​a1n​a2n​⋮amn​​ ​

• 当调用函数来实例化张量时，可通过指定两个分量 m 和 n 来创建一个形状为 m x n 的矩阵
• 当交换矩阵的行和列时，结果称为矩阵的转置 (transpose)，用 A.T 访问
  A ⊤ = [ a 11 a 21 … a m 1 a 12 a 22 … a m 2 ⋮ ⋮ ⋱ ⋮ a 1 n a 2 n … a m n ] \mathbf{A}^\top=\begin{bmatrix}a_{11}&a_{21}&\ldots&a_{m1}\\a_{12}&a_{22}&\ldots&a_{m2}\\\vdots&\vdots&\ddots&\vdots\\a_{1n}&a_{2n}&\ldots&a_{mn}\end{bmatrix} A⊤= ​a11​a12​⋮a1n​​a21​a22​⋮a2n​​……⋱…​am1​am2​⋮amn​​ ​
• 作为方阵的一种特殊类型对称矩阵 A ，等于其转置：$\mathbf{A}={\mathbf{A}}^{\top }$

  import torch
  
  A = torch.arange(20).reshape(5, 4)
  B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]]) # 对称矩阵
  
  print(A)
  print(A.T) # 访问矩阵的转置
  print(B == B.T)
  

2.3.4 张量

• 向量是标量的推广，矩阵是向量的推广，还可构建具有更多轴的数据结构：张量是描述具有任意数量轴的 n 维数组的通用方法。例如，向量是一阶张量，矩阵是二阶张量。张量用特殊字体的大写字母表示 (例如，X、Y 和 Z) 它们的索引机制与矩阵类似
• 当开始处理图像时，张量将变得更加重要，图像以 n 维数组形式出现，其中 3 个轴对应于高度、宽度，以及一个通道 (channel) 轴，用于表示颜色通道 (红色、绿色和蓝色)

  import torch
  
  a = 2
  X = torch.arange(24).reshape(2, 3, 4)
  
  print(X)
  print(a + X)
  print(a * X)
  

2.3.5 张量算法的基本性质

• 任何按元素的一元运算都不会改变其操作数的形状。同样，给定具有相同形状的任意两个张量，任何按元素二元运算的结果都将是相同形状的张量
• 两个矩阵的按元素乘法称为 Hadamard 积（数学符号 $\odot$）
  A ⊙ B = [ a 11 b 11 a 12 b 12 … a 1 n b 1 n a 21 b 21 a 22 b 22 … a 2 n b 2 n ⋮ ⋮ ⋱ ⋮ a m 1 b m 1 a m 2 b m 2 … a m n b m n ] \mathbf{A}\odot\mathbf{B}=\begin{bmatrix}a_{11}b_{11}&a_{12}b_{12}&\ldots&a_{1n}b_{1n}\\a_{21}b_{21}&a_{22}b_{22}&\ldots&a_{2n}b_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{m1}b_{m1}&a_{m2}b_{m2}&\ldots&a_{mn}b_{mn}\end{bmatrix} A⊙B= ​a11​b11​a21​b21​⋮am1​bm1​​a12​b12​a22​b22​⋮am2​bm2​​……⋱…​a1n​b1n​a2n​b2n​⋮amn​bmn​​ ​
• 将张量乘以或加上一个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘

  import torch
  
  A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
  B = A.clone() # 通过分配新内存，将 A 的一个副本分配给B
  
  # print(A + B)
  print(A * B)
  

2.3.6 降维

• 可以表示任意形状张量的元素和，矩阵 A 中元素的和可以记为 ${\sum }_{i=1}^m{\sum }_{j=1}^n{a}_{ij}$
• 默认情况下，调用求和函数会沿所有的轴降低张量的维度，使它变为一个标量。还可指定张量沿哪一个轴来通过求和降低维度
  • 以矩阵为例，为了通过求和所有行的元素来降维 (轴 0)，可以在调用函数时指定 axis=0
  • 指定 axis=1 将通过汇总所有列的元素降维 (轴 1)
• 与求和相关的量是平均值 (mean 或 average)，将总和除以元素总数来计算平均值。可调用函数来计算任意形状张量的平均值
• 计算平均值的函数也可以沿指定轴降低张量的维度

  import torch
  
  A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
  A_sum_axis0 = A.sum(axis=0)
  A_sum_axis1 = A.sum(axis=1)
  
  print(A.sum()) # 矩阵 A 中元素和
  print(A_sum_axis0)
  print(A_sum_axis1)
  print(A.mean())
  print(A.mean(axis=0))
  

非降维求和

• 有时在调用函数来计算总和或均值时保持轴数不变会很有用
• 如果想沿某个轴计算 A 元素的累积总和，比如 axis=0 (按行)，可以调用 cumsum 函数。此函数不会沿任何轴降低输入张量的维度

  import torch
  
  A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
  sum_A = A.sum(axis=1, keepdims=True) # 非降维（列）求矩阵 A 中元素和
  
  print(sum_A)
  print(A.cumsum(axis=0)) 
  

2.3.7 点积

• 给定两个向量 $\mathbf{x},\mathbf{y}\in {\mathbb{R}}^d$，它们的点积是相同位置的按元素乘积的和 ${\mathbf{x}}^{\top }\mathbf{y}={\sum }_{i=1}^d{x}_i{y}_i$

  import torch
  
  x = torch.arange(4, dtype=torch.float32)
  y = torch.ones(4, dtype=torch.float32)
  
  print(torch.dot(x, y))
  

• 点积在很多场合都很有用。例如，给定一组由向量 $\mathbf{x}\in {\mathbb{R}}^d$ 表示的值，和一组由 $\mathbf{w}\in {\mathbb{R}}^d$ 表示的权重。$\mathbf{x}$ 中的值根据权重 $\mathbf{w}$ 的加权和，可以表示为点积 ${\mathbf{x}}^{\top }\mathbf{w}$
  • 当权重为非负数且和为 1（即 $\left({\sum }_{\mathbf{i}=1}^d{w}_{\mathbf{i}}=1\right)$）时，点积表示加权平均 (weighted average)
  • 将两个向量规范化得到单位长度后，点积表示它们夹角的余弦

2.3.8 矩阵-向量积

• 定义矩阵 $\mathbf{A}\in {\mathbb{R}}^{m\times n}$ 和向量 $\mathbf{x}\in {\mathbb{R}}^n$，矩阵向量积 $\mathbf{Ax}$ 是一个长度为 m 的列向量
• 使用矩阵-向量积来描述在给定前一层的值时，求解神经网络每一层所需的复杂计算
  A x = [ a 1 ⊤ a 2 ⊤ ⋮ a m ⊤ ] x = [ a 1 ⊤ x a 2 ⊤ x ⋮ a m ⊤ x ] \mathbf{A}\mathbf{x}=\begin{bmatrix}\mathbf{a}_1^\top\\\mathbf{a}_2^\top\\\vdots\\\mathbf{a}_m^\top\end{bmatrix}\mathbf{x}=\begin{bmatrix}\mathbf{a}_1^\top\mathbf{x}\\\mathbf{a}_2^\top\mathbf{x}\\\vdots\\\mathbf{a}_m^\top\mathbf{x}\end{bmatrix} Ax= ​a1⊤​a2⊤​⋮am⊤​​ ​x= ​a1⊤​xa2⊤​x⋮am⊤​x​ ​

  import torch
  
  A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
  x = torch.arange(4, dtype=torch.float32)
  
  print(torch.mv(A, x)) # 使⽤ mv 函数执行矩阵-向量积
  

2.3.9 矩阵-矩阵乘法

• 假设两个 $\mathbf{A}\in {\mathbb{R}}^{n\times k}$ 和 $\mathbf{B}\in {\mathbb{R}}^{k\times m}$
  A = [ a 11 a 12 ⋯ a 1 k a 21 a 22 ⋯ a 2 k ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n k ] , B = [ b 11 b 12 ⋯ b 1 m b 21 b 22 ⋯ b 2 m ⋮ ⋮ ⋱ ⋮ b k 1 b k 2 ⋯ b k m ] \mathbf{A}=\begin{bmatrix}a_{11}&a_{12}&\cdots&a_{1k}\\a_{21}&a_{22}&\cdots&a_{2k}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nk}\end{bmatrix},\quad\mathbf{B}=\begin{bmatrix}b_{11}&b_{12}&\cdots&b_{1m}\\b_{21}&b_{22}&\cdots&b_{2m}\\\vdots&\vdots&\ddots&\vdots\\b_{k1}&b_{k2}&\cdots&b_{km}\end{bmatrix} A= ​a11​a21​⋮an1​​a12​a22​⋮an2​​⋯⋯⋱⋯​a1k​a2k​⋮ank​​ ​,B= ​b11​b21​⋮bk1​​b12​b22​⋮bk2​​⋯⋯⋱⋯​b1m​b2m​⋮bkm​​ ​

C = A B = [ a 1 ⊤ a 2 ⊤ ⋮ a n ⊤ ] [ b 1 b 2 ⋯ b m ] = [ a 1 ⊤ b 1 a 1 ⊤ b 2 ⋯ a 1 ⊤ b m a 2 ⊤ b 1 a 2 ⊤ b 2 ⋯ a 2 ⊤ b m ⋮ ⋮ ⋱ ⋮ a n ⊤ b 1 a n ⊤ b 2 ⋯ a n ⊤ b m ] \mathbf{C}=\mathbf{A}\mathbf{B}=\begin{bmatrix}\mathbf{a}_1^\top\\\mathbf{a}_2^\top\\\vdots\\\mathbf{a}_n^\top\end{bmatrix}\begin{bmatrix}\mathbf{b}_1&\mathbf{b}_2&\cdots&\mathbf{b}_m\end{bmatrix}=\begin{bmatrix}\mathbf{a}_1^\top\mathbf{b}_1&\mathbf{a}_1^\top\mathbf{b}_2&\cdots&\mathbf{a}_1^\top\mathbf{b}_m\\\mathbf{a}_2^\top\mathbf{b}_1&\mathbf{a}_2^\top\mathbf{b}_2&\cdots&\mathbf{a}_2^\top\mathbf{b}_m\\\vdots&\vdots&\ddots&\vdots\\\mathbf{a}_n^\top\mathbf{b}_1&\mathbf{a}_n^\top\mathbf{b}_2&\cdots&\mathbf{a}_n^\top\mathbf{b}_m\end{bmatrix} C=AB= ​a1⊤​a2⊤​⋮an⊤​​ ​[b1​​b2​​⋯​bm​​]= ​a1⊤​b1​a2⊤​b1​⋮an⊤​b1​​a1⊤​b2​a2⊤​b2​⋮an⊤​b2​​⋯⋯⋱⋯​a1⊤​bm​a2⊤​bm​⋮an⊤​bm​​ ​

• 可以将矩阵-矩阵乘法 $\mathbf{AB}$ 看作简单地执行 m 次矩阵-向量积

  import torch
  
  A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
  B = torch.ones(4, 3)
  
  print(torch.mm(A, B)) # 使⽤ mm 函数执行矩阵-矩阵乘法
  

2.3.10 范数

• 非正式地说，向量的范数 (norm) 是表示一个向量有多大。这里考虑的大小 (size) 概念不涉及维度，而是分量的大小

• 在线性代数中，向量范数是将向量映射到标量的函数 $f$。给定任意向量 $\mathbf{x}$，向量范数要满足一些属性

  • 第一个性质是: 如果按常数因子 $\alpha$ 缩放向量的所有元素，其范数也会按相同常数因子的绝对值缩放
    $$f(\alpha \mathbf{x})=|\alpha |f(\mathbf{x})$$
  • 第二个性质是三角不等式
    $$f(\mathbf{x}+\mathbf{y})\le f(\mathbf{x})+f(\mathbf{y})$$
  • 第三个性质是范数必须是非负的（范数最小为 0，当且仅当向量全由 0 组成）
    $$f(\mathbf{x})\ge 0$$

• 欧几里得距离是一个 $L_2$ 范数，假设 n 维向量 $\mathbf{x}$ 中的元素是 $x_1,...,x_n$，其 $L_2$ 范数是向量元素平方和的平方根

  • $L_2$ 范数中常常省略下标 2，也就是说 $\Vert \mathbf{x}\Vert$ 等同于 $\Vert \mathbf{x}{\Vert }_2$
    $$\Vert \mathbf{x}{\Vert }_2=\sqrt{\sum _{i=1}^n{x}_i^2}$$

• 深度学习中更经常地使用 $L_2$ 范数的平方，也会经常遇到 $L_1$ 范数，它表示为向量元素的绝对值之和
  $$\Vert \mathbf{x}{\Vert }_1=\sum _{i=1}^n|x_i|$$

• $L_2$ 范数和 $L_1$ 范数都是更一般的 $L_p$ 范数的特例
  $$\Vert \mathbf{x}{\Vert }_p={\left(\sum _{i=1}^n|x_i{|}^p\right)}^{1/p}$$

• 类似于向量的 $L_2$ 范数，矩阵 $\mathbf{X}\in {\mathbb{R}}^{m\times n}$ 的 Frobenius 范数是矩阵元素平方和的平方根

  • Frobenius范数满足向量范数的所有性质，它就像是矩阵形向量的 $L_2$ 范数
    $$\Vert \mathbf{X}{\Vert }_F=\sqrt{\sum _{i=1}^m\sum _{j=1}^n{x}_{ij}^2}$$

  import torch
  
  u = torch.tensor([3.0, 4.0])
  
  print(torch.norm(u))     # 计算 L2 范数
  print(torch.abs(u).sum)  # 计算 L1 范数
  print(torch.norm(torch.ones((4, 9)))) # 计算矩阵范数
  

  在深度学习中，经常试图解决优化问题：最大化分配给观测数据的概率，最小化预测和真实观测之间的距离。用向量表示物品(如单词、产品或新闻文章)，以便最小化相似项目之间的距离，最大化不同项目之间的距离。目标，通常被表达为范数

2.4 微积分

• 逼近法就是积分 (integral calculus) 的起源。微积分的另一支，微分 (differential calculus)在微分学最重要的应用是优化问题

• 在深度学习中 “训练” 模型，不断更新它们，使它们在看到越来越多的数据时变得越来越好。通常情况下，变得更好意味着最小化一个损失函数 (loss function)。最终生成一个模型，它能够在从未见过的数据上表现良好。但 “训练” 模型只能将模型与实际能看到的数据相拟合。因此，可以将拟合模型的任务分解为两个关键问题
  • 优化 (optimization)：用模型拟合观测数据的过程
  • 泛化 (generalization)：用数学原理和实践者的智慧，指导生成出有效性超出用于训练的数据集本身的模型

2.4.1 导数和微分

• 在深度学习中，通常选择对于模型参数可微的损失函数。简而言之，对于每个参数，如果把这个参数增加或减少一个无穷小的量，可以知道损失会以多快的速度增加或减少

• 假设有一个函数 $f:\mathbb{R}\to \mathbb{R}$，其输入和输出都是标量。如果 $f$ 的导数存在，这个极限被定义为
  $$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$

• 如果 $f^{\prime }(a)$ 存在，则称 $f$ 在 $a$ 处是可微 (differentiable) 的。如果 $f$ 在一个区间内的每个数上都是可微的，则此函数在此区间中是可微的。可将上式中的导数 $f^{\prime }(a)$ 解释为 $f(a)$ 相对于 $x$ 的瞬时变化率。所谓瞬时变化率是基于 $x$ 中的变化 $h$，且 $h$ 接近 0

• 导数的几个等价符号
  $$f^{\prime }(x)=y^{\prime }=\frac{dy}{dx}=\frac{df}{dx}=\frac{d}{dx}f(x)=Df(x)=D_{x}f(x)$$

• 其中 $\frac{d}{dx}$ 和 $D$ 是微分运算符，表示微分操作，常见微分法则如下
  $$\frac{d}{dx}[Cf(x)]=C\frac{d}{dx}f(x)$$

$$\frac{d}{dx}[f(x)+g(x)]=\frac{d}{dx}f(x)+\frac{d}{dx}g(x)$$

$$\frac{d}{dx}[f(x)g(x)]=f(x)\frac{d}{dx}[g(x)]+g(x)\frac{d}{dx}[f(x)]$$

$$\frac{d}{dx}\left[\frac{f(x)}{g(x)}\right]=\frac{g(x)\frac{d}{dx}[f(x)]-f(x)\frac{d}{dx}[g(x)]}{[g(x){]}^2}$$

• 下面以 $f(x)=3x^2-4x$ 为例来更好的解释导数

import numpy as np
import matplotlib.pyplot as plt

def f(x):
    return 3 * x ** 2 - 4 * x

def numerical_lim(f, x, h):
    return (f(x + h) - f(x)) / h

# 通过令 x = 1 并让 h 接近 0，则 numerical_lim 结果接近 2
h = 0.1
for i in range(5):
    # 将变量 h 格式化为浮点数，并保留小数点后五位
    print(f'h={h:.5f}, numerical limit={numerical_lim(f, 1, h):.5f}')
    h *= 0.1

# 定义 set_figsize 函数来设置图表大小
    # 参数 figsize 是一个长度为 2 的元组，用于指定图形的宽度和高度
    # plt.rcParams 是 Matplotlib 库中的一个全局变量，它是一个字典对象，存储了一些全局默认值
    # figure.figsize 是其中一个键值对，用于设置图形的尺寸，默认值为 (6.0, 4.0)
def set_figsize(figsize=(3.5, 2.5)):
    plt.rcParams['figure.figsize'] = figsize  # 修改全局默认值 figsize

# 用于设置由 matplotlib 生成图表的轴的属性
# axes：图形的轴对象（坐标轴）  legend：图例
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
    axes.set_xlabel(xlabel)  # x 轴的标签
    axes.set_ylabel(ylabel)  
    axes.set_xscale(xscale)  # x 轴的刻度缩放方式，可以是线性（linear）或对数（log）
    axes.set_yscale(yscale)
    axes.set_xlim(xlim)      # x 轴的范围
    axes.set_ylim(ylim)      
    if legend:               # 如果 legend 参数不为空
        axes.legend(legend)  # 则调用轴对象的 legend() 方法设置图例
    axes.grid()              # 使用 grid() 方法在图形中加入网格

# 定义一个 plot 函数来简洁地绘制多条曲线
# fmts：曲线的样式，可以是一条曲线的样式（字符串）或多条曲线的样式（字符串组成的列表）
    # ('-','m--')：这个字符串元组表示一个紫色 (m) 的虚线 (--) 
    # ('g-.')：这个字符串元组表示一个绿色 (g) 的点划线 (-.) 
    # ('r:')：这个字符串元组表示一个红色 (r) 的点线 (:) 
def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,
        ylim=None, xscale='linear', yscale='linear',
        fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):

    # 绘制数据点
    if legend is None:
        legend = []       # 设置图例为空列表
    set_figsize(figsize)  # 设置图标大小
    
    # 如果 X 只有⼀个轴，则输出 True
    def has_one_axis(X):
        # 判断 X 对象是否有一个属性 ndim，并且是否等于 1（即 X 是否为一维对象）
        # 判断 X 是否为 list 类型的对象，并且第一个元素是否没有属性 __len__（即判断 X 的第一个元素是否是一维对象）
        return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)
                and not hasattr(X[0], "__len__"))
    
    if has_one_axis(X):    # 如果 X 只有一个轴
        X = [X]            # 则将 X 放入一个列表中
    if Y is None:
        X, Y = [[]] * len(X), X  # X、Y 的初始值都是包含有 len(X) 个空列表的列表
    elif has_one_axis(Y):  # 如果 Y 只有一个轴
        Y = [Y]
    if len(X) != len(Y):   # 如果 X 和 Y 长度不等，则将 X 复制多份以匹配 Y 的长度
        X = X * len(Y)

    fig, ax = plt.subplots()  # 创建一个新的图形窗口，并返回一个包含 FigFig 对象和 Axes 对象的元组(fig, ax)
    # 遍历 X、Y 和 fmts 三个列表，并使用 zip 函数将它们中的元素一一对应起来
    for x, y, fmt in zip(X, Y, fmts):
        if len(x):              # x 列表不为空
            ax.plot(x, y, fmt)  # 则调用 ax.plot() 函数绘制 x 和 y 之间的数据点，并使用 fmt 参数指定样式
        else:                   # 如果 x 列表为空
            ax.plot(y, fmt)     # 则说明传入的是一个一维的 y 数组
    set_axes(ax, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
    plt.show()  # 显示图形窗口

# 绘制函数 f(x) 及其在 x = 1 处的切线 y = 2x - 3，其中系数 2 是切线的斜率
x = np.arange(0, 3, 0.1)  # 定义一个从 0 到 3，步长为 0.1 的数组 x
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])

# 输出
h=0.10000, numerical limit=2.30000
h=0.01000, numerical limit=2.03000
h=0.00100, numerical limit=2.00300
h=0.00010, numerical limit=2.00030
h=0.00001, numerical limit=2.00003

2.4.2 偏导数

• 在深度学习中，函数通常依赖于许多变量。因此，需要将微分的思想推广到多元函数

• 设 $y=f(x_1,x_2,\dots ,x_n)$ 是一个具有 $n$个变量的函数。$y$ 关于第 $i$ 个参数 $x_i$ 的偏导数 (partial derivative) 为
  $$\begin{array}{r}\frac{\partial y}{\partial x_i}=\underset{h\to 0}{\lim }\frac{f(x_1,\dots ,x_{i-1},x_i+h,x_{i+1},\dots ,x_n)-f(x_1,\dots ,x_i,\dots ,x_n)}{h}\end{array}$$

• 偏导数的几个等价符号
  $$\begin{array}{r}\frac{\partial y}{\partial x_i}=\frac{\partial f}{\partial x_i}=f_{x_i}=f_i=D_{i}f=D_{x_i}f\end{array}$$

2.4.3 梯度

• 可以连结一个多元函数对其所有变量的偏导数，以得到该函数的梯度 (gradient) 向量。具体而言，设函数 $f:{\mathbb{R}}^n\to \mathbb{R}$ 的输入是一个 $n$ 维向量 $\mathbf{x}=[x_1,x_2,\ldots,x_n]^\top $，并且输出是一个标量。函数 $f(x)$ 相对于 $x$ 的梯度是一个包含 $n$ 个偏导数的向量
  $${\nabla }_{\mathbf{x}}f(\mathbf{x})={\left[\frac{\partial f(\mathbf{x})}{\partial x_1},\frac{\partial f(\mathbf{x})}{\partial x_2},\dots ,\frac{\partial f(\mathbf{x})}{\partial x_n}\right]}^{\top }$$
• 假设 $x$ 为 $n$ 维向量，在微分多元函数时经常使用以下规则
  $${\nabla }_{\mathbf{x}}\mathbf{Ax}={\mathbf{A}}^{\top }$$

$${\nabla }_{\mathbf{x}}{\mathbf{x}}^{\top }\mathbf{A}=\mathbf{A}$$

$${\nabla }_{\mathbf{x}}{\mathbf{x}}^{\top }\mathbf{Ax}=(\mathbf{A}+{\mathbf{A}}^{\top })\mathbf{x}$$

$${\nabla }_x\Vert \mathbf{x}{\Vert }^2={\nabla }_x{\mathbf{x}}^{\top }\mathbf{x}=2\mathbf{x}$$

2.4.4 链式法则

• 上面方法可能很难找到梯度，因为在深度学习中，多元函数通常是复合的，所以难以应用上述任何规则来微分这些函数。但链式法则可以被用来微分复合函数
  • 先考虑单变量函数。假设函数 $y=f(u)$ 和 $u=g(x)$ 都是可微的，根据链式法则
    $$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$$
  • 考虑函数具有任意数量的变量的情况。假设可微分函数 $y$ 有变量 $u_1,u_2,\dots ,u_m$，其中每个可微分函数 $u_i$ 都有变量 $x_1,x_2,\dots ,x_n$。其中 $y$ 是 $x_1,x_2,\dots ,x_n$ 的函数
    $$\frac{\partial y}{\partial x_i}=\frac{\partial y}{\partial u_1}\frac{\partial u_1}{\partial x_i}+\frac{\partial y}{\partial u_2}\frac{\partial u_2}{\partial x_i}+\cdots +\frac{\partial y}{\partial u_m}\frac{\partial u_m}{\partial x_i}$$

2.5 自动微分

• 深度学习框架通过自动计算导数，即自动微分 (automatic differentiation) 来加快求导。实际中，根据设计好的模型，系统会构建一个计算图 (computational graph)，来跟踪计算是哪些数据通过哪些操作组合起来产生输出。自动微分使系统能够随后反向传播梯度。这里的反向传播 (backpropagate) 意味着跟踪整个计算图，填充关于每个参数的偏导数

2.5.1 一个简单的例子

• 假设对函数 $y=2{\mathbf{x}}^{\top }\mathbf{x}$ 关于列向量 $\mathbf{x}$ 求导

  import torch
  
  # 计算 y 关于 x 的梯度之前，需要⼀个地方来存储梯度，不会在每次对一个参数求导时都分配新的内存
  # 一个标量函数关于向量 x 的梯度是向量，并且与 x 具有相同的形状
  x = torch.arange(4.0, requires_grad=True)  # 等价于 x.requires_grad_(True) 
  y = 2 * torch.dot(x, x)
  y.backward()  # 调用反向传播函数来自动计算 y 关于 x 每个分量的梯度
  
  print(y)
  print(x.grad)  # 默认值是 None
  print(x.grad == 4 * x)  # y = 2(x^T)x 关于 x 的梯度应为 4x，此行代码为验证梯度计算是否正确
  

  # 输出
  tensor(28., grad_fn=<MulBackward0>)
  tensor([ 0.,  4.,  8., 12.])
  tensor([True, True, True, True])
  

2.5.2 非标量变量的反向传播

• 当 $y$ 不是标量时，向量 $y$ 关于向量 $x$ 的导数的最自然解释是一个矩阵。对于高阶和高维的 $y$ 和 $x$，求导的结果可以是一个高阶张量
• 但当调用向量的反向计算时通常会试图计算一批训练样本中每个组成部分的损失函数的导数，这里的目的不是计算微分矩阵而是单独计算批量中每个样本的偏导数之和
• 反向传播的目的是计算 $y$ 关于 $x$ 的导数，即求 $dy/dx$。根据链式法则，$dy/dx$ 等于 $dy/dz$ 乘以 $dz/dx$，其中 $z$ 是 $y$ 与 $x$ 的中间变量。另外，由于 $y$ 对于 $x$ 的偏导数是一个向量，因此反向传播返回的结果也是一个向量，并将结果存储在 $x.grad$ 中

  import torch
  
  x = torch.arange(4.0, requires_grad=True)
  y = 2 * torch.dot(x, x)
  y.backward()
  
  # 对⾮标量调⽤ backward 需要传⼊⼀个 gradient 参数，该参数指定微分函数关于 self 的梯度
  x.grad.zero_()  # 在默认情况下，PyTorch 会累积梯度，因此需要清除之前的值
  y = x * x
  # 给定 torch.ones(len(x)) 作为反向传播的输入，意味着将一个与 x 的长度相同的全 1 向量作为 y 对于自己的导数进行反向传播
  # 根据链式法则，这相当于求 dy/dy，即对 y 求导。由于 y 是一个函数，因此返回值将是与 x 的导数相关的向量
  y.sum().backward()  # 等价于 y.backward(torch.ones(len(x)))
  
  print(x.grad)
  

  # 输出
  tensor([0., 2., 4., 6.])
  

2.5.3 Python 控制流的梯度计算

• 使用自动微分的一个好处是：即使构建函数的计算图需要通过 Python 控制流 (例如，条件、循环或任意函数调用)，仍然可以计算得到的变量的梯度。在下面的代码中，while 循环的迭代次数和 if 语句的结果都取决于输入 a 的值

  import torch
  
  def f(a):
      b = a * 2
      while b.norm() < 1000:
          b = b * 2
          if b.sum() > 0:
              c = b
          else:
              c = 100 * b
          return c
  
  a = torch.randn(size=(), requires_grad=True)
  d = f(a)
  d.backward()
  
  print(a.grad == d / a)
  

  # 输出
  tensor(True)
  

2.6 概率

2.6.1 基本概率论

• 假设掷骰子，想知道看到 1 的几率有多大，如果骰子是公平的，那么所有六个结果 {1,…,6} 都有相同的可能发生，因此可以说 1 发生的概率为 1/6。大数定律 (law oflarge numbers) 告诉我们：随着投掷次数的增加，这个估计值会越来越接近真实的潜在概率
• 在统计学中，把从概率分布中抽取样本的过程称为抽样 (sampling)
  • 笼统来说，可以把分布 (distribution) 看作对事件的概率分配
  • 将概率分配给一些离散选择的分布称为多项分布 (multinomial distribution)
• 为掷骰子抽取一个样本，只需传入一个概率向量。输出另一个相同长度的向量：它在索引 i 处的值是采样结果中 i 出现的次数。可以模拟 1000 次投掷。然后统计 1000 次投掷后，每个数字被投中了多少次，计算相对频率，以作为真实概率的估计

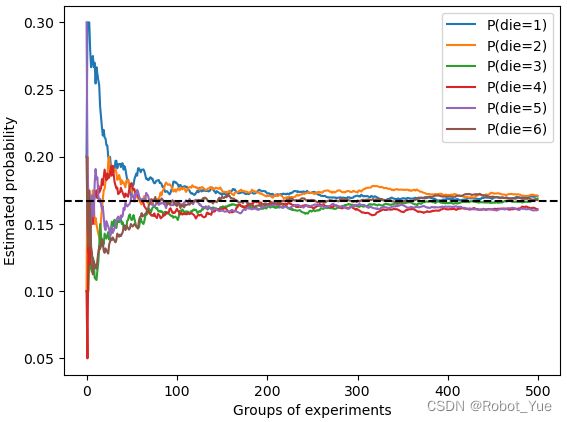
  import torch
  from torch.distributions import multinomial
  
  fair_probs = torch.ones([6]) / 6
  counts = multinomial.Multinomial(1000, fair_probs).sample()
  print(counts / 1000)  # 相对频率作为估计值
  

  # 输出（每个结果的真实概率约为 0.167）
  tensor([0.1600, 0.1840, 0.1700, 0.1650, 0.1670, 0.1540])
  

• 可以看到这些概率随着时间的推移收敛到真实概率，进行 500 组实验，每组抽取 10 个样本。每条实线对应于骰子的 6 个值中的一个，并给出骰子在每组实验后出现值的估计概率。当通过更多的实验获得更多的数据时，这 6 条实体曲线向真实概率收敛

  import torch
  import matplotlib.pyplot as plt
  from torch.distributions import multinomial
  
  fair_probs = torch.ones([6]) / 6
  counts = multinomial.Multinomial(10, fair_probs).sample((500,))
  cum_counts = counts.cumsum(dim=0)
  estimates = cum_counts / cum_counts.sum(dim=1, keepdim=True)
  
  def set_figsize(figsize=(6, 4.5)):
      plt.rcParams['figure.figsize'] = figsize
  
  for i in range(6):
      plt.plot(estimates[:, i].numpy(), label=("P(die=" + str(i + 1) + ")"))
  
  set_figsize((6, 4.5))
  plt.axhline(y=0.167, color='black', linestyle='dashed')
  plt.xlabel('Groups of experiments')
  plt.ylabel('Estimated probability')
  plt.legend()
  plt.show()  # plt.legend() 需要调用 plt.show() 来显示图例
  

概率论公理

• 在处理骰子掷出时，将集合 $\mathcal{S}=\{1,2,3,4,5,6\}$ 称为样本空间 (sample space) 或结果空间(outcomespace)，其中每个元素都是结果。事件 (event) 是一组给定样本空间的随机结果。例如，“看到 5”({5}) 和 “看到奇数” ({1,3,5}) 都是掷出骰子的有效事件
• 概率 (probability) 可认为是将集合映射到真实值的函数。在给定的样本空间 $\mathcal{S}$ 中，事件 $A$ 的概率表示为 $P(A)$，满足以下
  • 对于任意事件 $A$，其概率从不会是负数，即 $P(A)>0$
  • 整个样本空间的概率为 1，即 $P(\mathcal{S})=1$
  • 对于互斥 (mutually exclusive) 事件有：$P(A_1\cup A_2\cup A_3\cup…) = P(A_1)+P(A_2)+P(A_3)+\cdots $

随机变量

• 在掷散子的随机实验中，引入了随机变量 (random variable) 概念。随机变量几乎可以是任何数量，并且它可以在随机实验的一组可能性中取一个值。考虑一个随机变量 $X$，其值在掷骰子的样本空间 $\mathcal{S}=\{1,2,3,4,5,6\}$ 中。可以将事件 “看到一个5” 表示为 $\{X=5\}$ 或 $X=5$，其概率表示为 $P(\{X=5\})$ 或 $P(X=5)$

  • 可以将 $P(X)$ 表示为随机变量 $X$ 上的分布 (distribution)，分布表示 $X$ 获得某⼀值的概率
  • 可以用 $P(a)$ 表示随机变量取值 $a$ 的概率

• 由于概率论中的事件是来自样本空间的一组结果，因此可以为随机变量指定值的可取范围。例如，$P(1\le X\le 3)$ 表示事件 $\{1\le X\le 3\}$，即 $\{X=1,2,\mathrm{or},3\}$ 的概率。等价地，$P(1\le X\le 3)$ 表示随机变量 $X$ 从 $\{1,2,3\}$ 中取值的概率

• 离散（discrete）随机变量（如骰⼦的每⼀⾯）和连续（continuous）随机变量（如人的体重和身高）之间存在微妙的区别，以下小节主要考虑离散空间中的概率，连续随机变量的概率参考：连续随机变量

2.6.2 处理多个随机变量

联合概率

• 联合概率 (joint probability)：$P(A=a,B=b)$
  • 给定任意值 $a$ 和 $b$，$A=a$ 和 $B=b$ 同时满足的概率
  • 对于任何 $a$ 和 $b$ 的取值，满足：$P(A=a,B=b)\le P(A=a)$ 与 $P(A=a,B=b)\le P(B=b)$

条件概率

• 联合概率的不等式带来一个有趣的比率：$0\le \frac{P(A=a,B=b)}{P(A=a)}\le 1$，称这个比率为条件概率 (conditional probability)，并用 $P(B=b\mid A=a)$ 表示它：$A=a$ 已发生的前提下，$B=b$ 发生的概率

贝叶斯定理

• 根据条件概率和乘法法则
  $$P(A,B)=P(B\mid A)P(A)$$

$$P(A,B)=P(A\mid B)P(B)$$

• 于是得到贝叶斯定理
  $$P(A\mid B)=\frac{P(B\mid A)P(A)}{P(B)}$$

  $P(A,B)$ 是一个联合分布，$P(A\mid B)$ 是一个条件分布

边际化

• 为了能进行事件概率求和，需要求和法则，即 $B$ 的概率相当于计算 $A$ 的所有可能选择，并将所有选择的联合概率聚合在一起，这也称为边际化 (marginalization)。边际化结果的概率或分布称为边际概率或边际分布
  $$P(B)=\sum _{A}P(A,B)$$

独立性

• 如果两个随机变量 $A$ 和 $B$ 是独立的，意味着事件 $A$ 的发生跟 $B$ 事件的发生无关
  • 在这种情况下，通常将这一点表述为 $A\perp B$
  • 根据贝叶斯定理，马上就能同样得到 $P(A\mid B)=P(A)$
• 由于 $P(A\mid B)=\frac{P(A,B)}{P(B)}=P(A)$ 等价于 $P(A,B)=P(A)P(B)$
  • 因此两个随机变量是独立的，当且仅当：两个随机变量的联合分布是其各自分布的乘积
• 给定另一个随机变量 $C$ 时，两个随机变量 $A$ 和 $B$ 是条件独立的 (conditionally independent)，当且仅当 $P(A,B\mid C)=P(A\mid C)P(B\mid C)$
  • 这个情况表示为 $A\perp B\mid C$

2.6.3 期望和方差

• 为了概括概率分布的关键特征，需要一些测量方法。一个随机变量 $X$ 的期望 (expectation，或平均值 (average))
  $$E[X]=\sum _{x}xP(X=x)$$

• 当函数 $f(x)$ 的输入是从分布 $P$ 中抽取的随机变量时，$f(x)$ 的期望值为
  $$E_{x\sim P}[f(x)]=\sum _{x}f(x)P(x)$$

• 在许多情况下，希望衡量随机变量 $X$ 与其期望值的偏置，这可以通过方差来量化
  $$\mathrm{Var}[X]=E\left[(X-E[X]{)}^2\right]=E[X^2]-E[X{]}^2$$

  方差的平方根被称为标准差 (standard deviation)

• 随机变量函数的方差衡量的是：当从该随机变量分布中采样不同值 $x$ 时，函数值偏离该函数的期望的程度
  $$\mathrm{Var}[f(x)]=E\left[{\left(f(x)-E[f(x)]\right)}^2\right]$$