Python 中的回归树

在上一章关于分类决策树的章节中，我们介绍了决策树模型的基本概念，如何使用 Python 从头开始​​构建它们，以及使用预先打包的 sklearn DecisionTreeClassifier 方法。我们还介绍了决策树模型的优缺点以及重要的扩展和变体。分类决策树的一个缺点是它们需要一个分类缩放的目标特征，例如天气 = {晴天、雨天、阴天、雷雨}。

这里出现了一个问题：例如，如果我们希望我们的树根据房间数量和位置等一些目标特征属性来预测房屋的价格，该怎么办？这里目标特征（奖品）的值不再按类别缩放，而是连续的——理论上，房子可以有无数种不同的价格——

这就是回归树的用武之地。回归树的工作原理与分类树相同，区别在于目标特征值现在可以采用无限数量的连续缩放值。因此，现在的任务是在给定一组分类（或连续）缩放的描述性特征 X 的值的情况下预测连续缩放的目标特征 Y 的值。

如上所述，构建回归树的原理与创建分类树的方法相同。

我们搜索最纯粹地分割目标特征值的描述性特征，沿着这个描述性特征的值划分数据集，并对每个子数据集重复这个过程，直到我们完成一个停止标准。如果我们完成一个停止标准，我们生长一个叶子节点。

尽管如此，一些事情发生了变化。

首先，让我们考虑一下我们在分类树章节中介绍的用于生长叶节点的停止标准：

1. 如果拆分过程导致空数据集，则返回原始数据集的模式目标特征值
2. 如果分裂过程导致没有特征的数据集，则返回直接父节点的模式目标特征值
3. 如果拆分过程导致目标特征值纯的数据集，则返回此值

如果我们现在考虑新的连续缩放目标特征的属性，我们会提到不能再使用第三个停止标准，因为目标特征值现在可以采用无限数量的不同值。因此，在数据集中只剩下一个实例之前，我们很可能不会找到纯目标特征值。

长话短说，一般来说没有什么比纯目标特征值更好的了。

为了解决这个问题，我们将引入一个提前停止标准，如果数据集中的实例数为 ≤5.

通常，在处理回归树时，我们将返回平均目标特征值作为叶节点的预测。

当我们考虑拆分过程本身时，我们必须进行的第二个更改变得明显。

在使用分类树时，我们使用特征的信息增益 (IG) 作为分割标准。也就是说，使用具有最大 IG 的特征来分割数据集。考虑以下示例，其中我们仅检查一个描述性特征，例如卧室数量和作为目标特征的房屋成本。

将 熊猫 导入为 pd
将 numpy 导入为 np

df  =  pd 。数据帧（{ 'Number_of_Bedrooms' ：[ 2 ，2 ，4 ，1 ，3 ，1 ，4 ，2 ]，'Price_of_Sale' ：[ 100000 ，120000 ，250000 ，80000 ，220000 ，170000 ，500000 ，75000 ]}）
DF

现在我们如何计算Number_of_Bedrooms特征的熵？

H(N你米乙电子r ○F 乙电子dr○○米秒)=∑j ∈ N你米乙电子r ○F 乙电子dr○○米秒＊(|DN你米乙电子r ○F 乙电子dr○○米秒=j||D|＊(∑克 ∈ 磷r一世C电子 ○F 秒一个升电子＊(-磷(克 | j)＊升○G2(磷(克 | j)))))

如果我们计算加权熵，我们会看到对于 j = 3，我们得到的加权熵为 0。我们得到这个结果是因为数据集中只有一所房子有 3 间卧室。另一方面，对于 j = 2（出现 3 次），我们将得到 0.59436 的加权熵。

长话短说，由于我们的目标特征是连续缩放的，分类缩放的描述性特征的 IG 不再是合适的分割标准。

好吧，我们可以改为按照其值对目标特征进行分类，例如房价介于$0和之间$80000被归类为低、介于$80001和$150000中以及 >$150001高。

我们在这里所做的是将回归问题转化为分类问题。但是，由于我们希望能够从无限数量的可能值（回归）中进行预测，这不是我们想要的。

让我们回到我们最初的问题：我们想要一个分裂标准，它允许我们以这样的方式分裂数据集，当到达树节点时，预测值（我们将预测值定义为在此叶节点上的实例（我们将 5 个实例的最小数量定义为提前停止标准）最接近实际值。

事实证明，方差是回归树最常用的分割标准之一，我们将使用方差作为分割标准。

因此，解释是，当沿着这些目标特征的值分割数据集时，我们想要搜索最准确地指向真实目标特征值的特征属性。因此，请检查以下图片。您认为Number_of_Bedrooms功能的这两种布局中的哪一种更准确地指向真正的销售奖？

嗯，显然是方差最小的那个！我们将在下一节介绍方差度量背后的数学原理。

目前，我们首先用箭头说明这些，其中宽箭头代表高方差，细箭头代表低方差。我们可以通过显示描述性特征的每个值的目标特征的方差来说明这一点。如您所见，当我们沿着描述性特征的值分割数据集时，最小化目标特征值方差的特征布局是最准确地指向真实值的特征布局，因此应该用作分割标准。在创建回归树模型期间，我们将使用方差度量来代替信息增益作为拆分标准。

回归树背后的数学

如上所述，生长回归树期间的任务原则上与创建分类树期间的任务相同。但是，由于目标特征的连续性，IG 不再是合适的分割标准（基尼指数也不是），我们必须有一个新的分割标准。

因此我们使用我们现在要介绍的方差。

方差

伏一个r(X)=∑一世 =1n(是一世-是¯)n-1

在哪里 是一世 是单个目标特征值和 是¯ 是这些目标特征值的平均值。

以上面的例子为例，Prize_of_Sale目标特征的总方差计算公式为：

伏一个r(磷r一世C电子 ○F 秒一个升电子)=(100000-189375)2+(120000-189375)2+(250000-189375)2+(80000-189375)2+(220000-189375)2+(170000-189375)2+(500000-189375)2+(75000-189375)27

=19.903125＊109 #Large Number ;) 虽然这对我们的计算没有影响

由于我们想知道哪个描述性特征最适合分割目标特征，我们必须计算描述性特征的每个值相对于目标特征值的方差。

因此，对于上面的Number_of_Rooms描述性特征，我们得到了单个房间数：

伏一个r(N你米乙电子r ○F 电阻○○米秒 = 1)=(80000-125000)2+(170000-125000)21=4050000000

伏一个r(N你米乙电子r ○F 电阻○○米秒 = 2)=(100000-98333.3)2+(120000-98333.3)2+(75000-98333.3)22=508333333.3

伏一个r(N你米乙电子r ○F 电阻○○米秒 = 3)=(220000-220000)2=0

伏一个r(N你米乙电子r ○F 电阻○○米秒 = 4)=(250000-375000)2+(500000-375000)21=31250000000

由于我们现在还想解决这样一个问题，即存在相对较少出现但具有高方差的特征值（这可能导致整个特征的方差非常高，仅仅因为一个轮廓特征值，即使所有其他特征值的方差特征值可能很小）我们通过计算每个特征值的加权方差来解决这个问题：

宽电子一世GH吨伏一个r(N你米乙电子r ○F 电阻○○米秒 = 1)=28＊4050000000=1012500000

宽电子一世GH吨伏一个r(N你米乙电子r ○F 电阻○○米秒 = 2)=28＊508333333.3=190625000

宽电子一世GH吨伏一个r(N你米乙电子r ○F 电阻○○米秒 = 3)=28＊0=0

宽电子一世GH吨伏一个r(N你米乙电子r ○F 电阻○○米秒 = 4)=28＊31250000000=7812500000

最后，我们总结这些加权方差以对整个特征进行评估：

秒你米伏一个r(F电子一个吨你r电子)=∑v一个升你电子 ∈ F电子一个吨你r电子宽电子一世GH吨伏一个r(F电子一个吨你r电子v一个升你电子)

在我们的情况下：

1012500000+190625000+0+7812500000=9015625000

将所有这些放在一起最终得出加权特征方差的公式，我们将在拆分过程中的每个节点使用该公式来确定我们应该选择下一步拆分数据集的特征。

F电子一个吨你r电子[CH○○秒电子] =精氨酸F ∈ F电子一个吨你r电子秒 ∑升 ∈ 升电子v电子升秒(F)|F=升||F|＊伏一个r(吨,F=升)

=精氨酸F ∈ F电子一个吨你r电子秒 ∑升 ∈ 升电子v电子升秒(F)|F=升||F|＊∑一世 = 1n(吨一世-吨¯)2n-1

这里f表示单个特征，l表示特征的值（例如价格 == 中等），t表示子集中目标特征的值，其中f=l。

按照这个计算规范，我们在每个节点找到特征来分割我们的数据集。

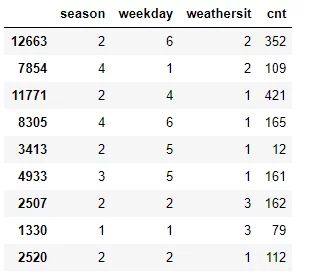
为了说明沿最低方差特征的特征值拆分数据集的过程，我们以UCI 共享单车数据集的简化示例为例，稍后我们将在回归树中使用本章的Python部分从头开始并计算每个特征的方差以找到我们应该用作根节点的特征。

将 熊猫 导入为 pd

df  =  pd 。read_csv ( "data/day.csv" , usecols = [ 'season' , 'holiday' , 'weekday' , ' weathersit ' , 'cnt' ]) 
df_example  =  df 。样本（分数= 0.012 ）

季节

宽电子一世GH吨伏一个r(秒电子一个秒○n)=19＊(79-79)2+59＊(352-211.8)2+(421-211.8)2+(12-211.8)2+(162-211.8)2+(112-211.8)24+19＊(161-161)2+29＊(109-137)2+(165-137)21

=16429.1

工作日