Java【动态规划】图文详解 “路径问题模型“ , 教你手撕动态规划
文章目录
- 一、不同路径I
-
- 1, 题目
- 2, 思路分析
-
- 2.1, 状态表示
- 2.2, 状态转移方程
- 2.3, 初始化
- 2.4, 填表顺序
- 2.5, 返回值
- 3, 代码
- 二、不同路径II
-
- 1, 题目
- 2, 思路分析
-
- 2.1, 状态表示
- 2.2, 状态转移方程
- 2.3, 初始化
- 2.4, 填表顺序
- 2.5, 返回值
- 3, 代码
- 三、礼物最大价值
-
- 1, 题目
- 2, 思路分析
-
- 2.1, 状态表示
- 2.2, 状态转移方程
- 2.3, 初始化
- 2.4, 填表顺序
- 2.5, 返回值
- 3, 代码
- 四、下降路径最小和
-
- 1, 题目
- 2, 思路分析
-
- 2.1, 状态表示
- 2.2, 状态转移方程
- 2.3, 初始化
- 2.4, 填表顺序
- 2.5, 返回值
- 3, 代码
- 五、最小路径和
-
- 1, 题目
- 2, 思路分析
-
- 2.1, 状态表示
- 2.2, 状态转移方程
- 2.3, 初始化
- 2.4, 填表顺序
- 2.5, 返回值
- 3, 代码
- 五、地下城游戏(较难)
-
- 1, 题目
- 2, 思路分析
-
- 2.1, 状态表示
- 2.2, 状态转移方程
- 2.3, 初始化
- 2.4, 填表顺序
- 2.5, 返回值
- 3, 代码
本篇总结动态规划中的路径问题模型的解法和思路
按照以下流程进行分析题目和代码编写
| 思路分析步骤 | 代码编写步骤 |
|---|---|
| 1, 状态表示 | 1, 构造 dp 表 |
| 2, 状态转移方程 | 2, 初始化+边界处理 |
| 3, 初始化 | 3, 填表(抄状态转移方程) |
| 4, 填表顺序 | 4, 返回结果 |
| 5, 返回值 | / |
一、不同路径I
1, 题目
OJ链接
题目分析: 从二位数组的左上角到右下角的路径总数, 只能往下或往右
2, 思路分析
2.1, 状态表示
根据题目要求, 要我们算出到右下角的路径条数, 我们要构造一个dp表(二位数组), 表中的某个值就是我们想要的结果, 如果我们能先算出到达网格中任意位置的路径总数, 那么也能算出右下角的路径总数
状态表示 : 以 [i][j] 位置为终点, dp[i][j] 就是走到 [i][j] 位置时的路径总数
2.2, 状态转移方程
以 [i][j] 位置状态的最近的⼀步,来分情况讨论
要到达某个位置, 有两种方式 : 从上边过来或从左边过来, 所以 dp[i][j] 依赖上边和左边两个位置的值
- 如果 : 起点 --> 当前位置的上方的路径总数 = X, 那么 : 起点 --> 当前位置的路径总数 = X
(X = dp[i - 1][j]) - 如果 : 起点 --> 当前位置的左方的路径总数 = Y, 那么 : 起点 --> 当前位置的路径总数 = Y
(Y = dp[i][j - 1])
所以 : 起点 --> 当前位置的路径总数 = X + Y, 那么状态转移方程 : dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
注意理解, 为啥从起点 --> 当前位置的上方的路径总数 = X, 那么从起点 --> 当前位置路径总数不是 = X + 1 ?
因为从上方到当前位置只是需要多走一步, 而不是多了一种方式
比如从市中心到火车站有 4 种方式 : 骑自行车, 骑电动车, 坐公交车, 坐出租车, 这些才是方式, 哪怕下了车之后再走 100 步才能真正到火车站检票口, 也只有 4 种方式
2.3, 初始化
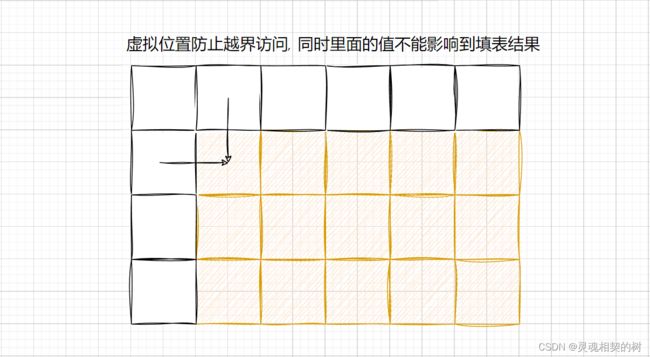
初始化是为了填表的时候不越界访问
根据状态转移方程可以分析出, dp[i][j] 依赖上面和左面值, 所以在表中的第一行和第一列的值需要手动填
更推荐的方式是 : 给出虚拟位置, 也就是建表的时候多建一行, 一列, 经过分析, 把 dp[0][1] 位置初始化成 1 即可(虽然看似没有第一种方式简单, 但对于更复杂的 dp 问题, 使用虚拟位置的方式可能反而会更容易)
使用添加虚拟位置辅助初始化的方式, 一定要注意和原表中的下标映射关系!!
初始化 : dp[0][1] = 1
2.4, 填表顺序
由于dp[i][j] 依赖上面和左面值, 所以填表顺序是从上到下, 从左往右
2.5, 返回值
要我们求到达右下角的路径总数, 就是 dp[m][n]
题目给定的网格大小是 m X n 大小的, 那么右下角的坐标对应到二维数组中应该是 [m - 1][n - 1]
但是我们初始化时选择多加一行一列, 所以返回 [m][n] 下标的值正好是原来表中的右下角
3, 代码
public int uniquePaths(int m, int n) {
// 构造dp表
int[][] dp = new int[m + 1][n + 1];
// 初始化
dp[0][1] = 1;
// 填表 (抄状态转移方程)
for(int i = 1; i <= m; i++ ) {
for(int j = 1; j <= n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
// 返回值
return dp[m][n];
}
二、不同路径II
1, 题目
OJ链接
和上题基本一致, 只是多了一个障碍物, 障碍物无法到达, 所以 dp 表中这个位置的值必须填成 0
2, 思路分析
2.1, 状态表示
参考上题
状态表示 : 以 [i][j] 位置为终点, dp[i][j] 就是走到 [i][j] 位置时的路径总数
2.2, 状态转移方程
以 [i][j] 位置状态的最近的⼀步,来分情况讨论 参考上题 :
(需注意 : 每个位置都要判断此位置是否为障碍物, 如果为障碍物, dp[i][j] 置为 0 , 否则 : )
状态转移方程 : dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
2.3, 初始化
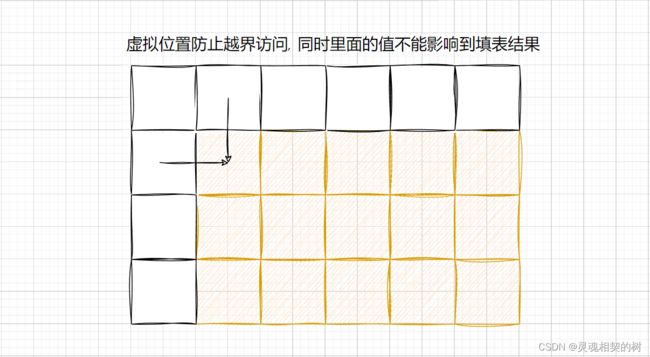
初始化是为了填表的时候不越界访问
参考上题 : 初始化 : dp[0][1] = 1
2.4, 填表顺序
同上题, 由于dp[i][j] 依赖上面和左面值, 所以填表顺序是从上到下, 从左往右
2.5, 返回值
要我们求到达右下角的路径总数, 就是 dp[m][n]
题目给定的网格大小是 m X n 大小的, 那么右下角的坐标对应到二维数组中应该是 [m - 1][n - 1]
但是我们初始化时选择多加一行一列, 所以返回 [m][n] 下标的值正好是原来表中的右下角
3, 代码
注意判断障碍物
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
// 构造dp表
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m + 1][n + 1];
// 初始化
dp[0][1] = 1;
// 填表
for( int i = 1; i <= m; i++) {
for(int j = 1; j <= n; j++) {
// 先判断当前位置是否为障碍物
if(obstacleGrid[i - 1][j - 1] == 0) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}else {
dp[i][j] = 0;
}
}
}
// 返回值
return dp[m][n];
}
三、礼物最大价值
1, 题目
OJ链接
和前两题不同, 本题要求的是走到右下角位置时, 路径上的最大和
2, 思路分析
2.1, 状态表示
我们需要构造 dp 表, 要求最终的路径最大和, 划分子问题后 : 可以先求出到达途中任意位置的最大和(每次都是二选一, 取最优解)
所以 状态表示 : 以 [i][j] 位置为终点, dp[i][j] 表示该路径上的最大和
2.2, 状态转移方程
以 [i][j] 位置状态的最近的⼀步,来分情况讨论, 要求 dp[i][j], 有两种情况
- 从 上方 过来 :
( dp 表中)以上方为终点时的最大和 +(原表中)此位置的礼物价值 - 从 左方 过来 :
( dp 表中)以左方为终点时的最大和 +(原表中)此位置的礼物价值
要保证到达 [i][j] 位置时, 获取的礼物价值总和最大, 就要对这两种方式的结果取最大值
状态转移方程 : dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + 当前位置的礼物价值
2.3, 初始化
初始化是为了填表的时候不越界访问
参考前两题, 同样可以使用添加虚拟位置的方式辅助初始化, 但要保证 : 由于本题求的是"最大值", 前面也分析了每个位置的都要保证取到 “左” 和 “上” 二者较大值, 所以虚拟位置中的值不能影响到填表过程的取值情况
按理说, 虚拟位置的值填成
Integer.MIN_VALUE就能保证不被干扰, 但题目中已经说明了所有的礼物价值 > 0 , 所以虚拟位置无需初始化, 默认值为 0 也可以
使用添加虚拟位置辅助初始化的方式, 一定要注意和原表中的下标映射关系!!
2.4, 填表顺序
同上题, 由于dp[i][j] 依赖上面和左面值, 所以填表顺序是从上到下, 从左往右
2.5, 返回值
要我们求到达右下角时的最大和, 就是 dp[m][n]
3, 代码
状态转移方程为 : dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + 当前位置的礼物价值
当前位置的礼物价值在原表中,一定要注意原表中的下标和我们构造的(添加了虚拟位置)的 dp 表的下标映射关系
public int maxValue(int[][] grid) {
// 创建dp表
int m = grid.length;
int n = grid[0].length;
int[][] dp = new int[m + 1][n + 1];
// 初始化
// 填表
for(int i = 1; i <= m; i++) {
for(int j = 1; j <= n; j++) {
// 注意dp表的下标和grid表的下标映射关系!!
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + grid[i-1][j-1];
}
}
return dp[m][n];
}
四、下降路径最小和
1, 题目
OJ链接
从任意位置下降时, 只能走正下方, 或左下角, 或右下角
2, 思路分析
2.1, 状态表示
我们要求下降到最底下一层时, 最小的下降路径和, 划分子问题 : 我们可以求出(从第一层任意位置出发) 到任意位置的最小下降路径和, 然后再求出到最后一层的结果
状态表示 : 以 [i][j] 位置为终点, dp[i][j]表示到达 [i][j] 位置时 下降路径的最小和
2.2, 状态转移方程
以 [i][j] 位置状态的最近的⼀步,来分情况讨论, 要到达 [i][j] 位置, 有三种方式 :
-
从 [i][j] 位置的正上方下来
-
从 [i][j] 位置的左上角下来
-
从 [i][j] 位置的右上角下来
结合状态表示可知 : 位于 [i][j] 位置的正上方时, 也就是 [i - 1][j] 位置的最小下降路径和可以用 dp[i - 1][j] 来表示, 那么 `这种情况下 dp[i][j] 的值就是 dp[i - 1][j] 的值加上, 原表中 [i][j] 位置的值, 所以, 要求 dp[i][j] 就分为三种情况
- 从 [i][j] 位置的正上方下来时 : dp[i][j] = dp[i - 1][j] + 原表中 [i][j] 的值
- 从 [i][j] 位置的左上角下来时 : dp[i][j] = dp[i - 1][j - 1] + 原表中 [i][j] 的值
- 从 [i][j] 位置的右上角下来时 : dp[i][j] = dp[i - 1][j + 1] + 原表中 [i][j] 的值
所以状态转移方程 : dp[i][j] = (dp[i - 1][j], dp[i - 1][j - 1], dp[i - 1][j + 1])三者最小值 + 原表中 [i][j] 的值
2.3, 初始化
初始化是为了填表的时候不越界访问
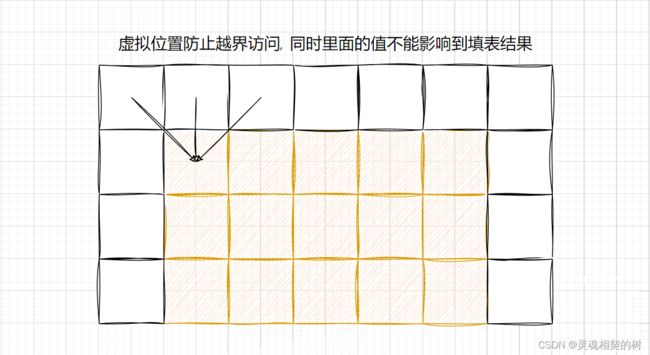
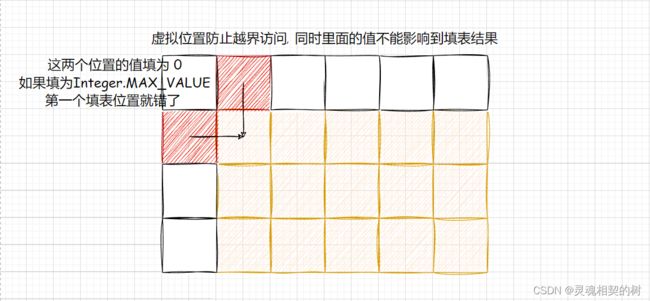
和前面的题类似, 给出虚拟位置, 根据前面的分析可知, 第一行, 第一列, 和最后一列, 套用状态转移方程时, 就会越界访问, 所以我们虚拟出这些位置, 相当于把原来的表半包围着
题中示例说明了, 原表中的值有可能时复数, 那我们虚拟位置的值默认成 0 还可行吗? 答案是否定的, 我们应该把虚拟位置中第一列和最后一列的值都初始化成 Integer.MAX_VALUE
使用添加虚拟位置辅助初始化的方式, 一定要注意和原表中的下标映射关系!!
初始化 : 第一列和最后一列的值为 Integer.MAX_VALUE
2.4, 填表顺序
填表顺序是从上到下
2.5, 返回值
和前面的题不同, 本题只要到达最后一行即可, 所以应该返回dp 表中最后一行的最小值
3, 代码
public int minFallingPathSum(int[][] matrix) {
// 创建dp表
int n = matrix.length;
int[][] dp = new int[n + 1][n + 2];
// 初始化
for(int i = 1; i <= n; i++) {
dp[i][0] = Integer.MAX_VALUE;
dp[i][n + 1] = Integer.MAX_VALUE;
}
// 填表
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
dp[i][j] = Math.min(dp[i - 1][j],
Math.min(dp[i - 1][j - 1], dp[i - 1][j + 1])) + matrix[i -1][j -1];
}
}
// 返回值
int ret = Integer.MAX_VALUE;
for(int i = 1; i <= n; i++) {
ret = Math.min(ret, dp[n][i]);
}
return ret;
}
五、最小路径和
1, 题目
OJ链接
题目分析: 从二位数组的左上角到右下角的路径总和, 只能往下或往右
本篇第一题是求路径总数, 这一题是求路径总和
2, 思路分析
2.1, 状态表示
划分子问题思想, 先求出从起点到达任意位置的路径总数, 把 dp 表填满, 右下角的值即为所求
状态表示 : 以 [i][j] 位置为终点, dp[i][j] 就是走到 [i][j] 位置时的路径总和
2.2, 状态转移方程
以 [i][j] 位置状态的最近的⼀步,来分情况讨论
要到达某个位置, 有两种方式 : 从上边过来或从左边过来, 所以 dp[i][j] 依赖上边和左边两个位置的值
- 如果 : 起点 --> 当前位置的上方的路径总和 = X, 那么 : 起点 --> 当前位置的路径总和 = X + 原表中当前位置的值
(X = dp[i - 1][j]) - 如果 : 起点 --> 当前位置的左方的路径总和 = Y, 那么 : 起点 --> 当前位置的路径总和 = Y + 原表中当前位置的值
(Y = dp[i][j - 1])
所以状态转移方程 : dp[i][j] = (dp[i - 1][j] , dp[i][j - 1]) 取最小值 + 原表中当前位置的值
2.3, 初始化
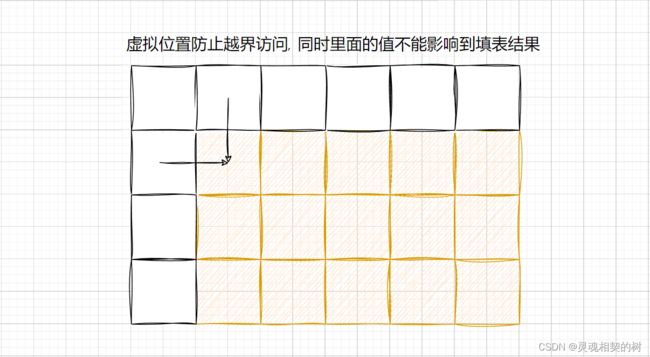
初始化是为了填表的时候不越界访问
给出虚拟位置 , 建表的时候多建一行, 一列, 经过分析, 每次都要取最小值, 所以虚拟位置的值应该填为 Integer.MAX_VALUE, 但第一行的 [1] 下标和第一列的 [1] 下标需要设置成 0
使用添加虚拟位置辅助初始化的方式, 一定要注意和原表中的下标映射关系!!
初始化 : 第一行第一列的值为 Integer.MAX_VALUE, dp[0][1] = 1 , dp[1][0] = 1
2.4, 填表顺序
由于dp[i][j] 依赖上面和左面值, 所以填表顺序是从上到下, 从左往右
2.5, 返回值
要我们求到达右下角的路径总和, 就是 dp[m][n]
3, 代码
public int minPathSum(int[][] grid) {
// 1, 构造dp表
int m = grid.length;
int n = grid[0].length;
int[][] dp = new int[m + 1][n + 1];
// 2, 初始化
for(int i = 0; i <= m;i++) {
dp[i][0] = Integer.MAX_VALUE;
}
for(int i = 0; i <= n;i++) {
dp[0][i] = Integer.MAX_VALUE;
}
dp[0][1] = 0;
dp[1][0] = 0;
// 3, 填表
for(int i = 1; i <= m; i++) {
for(int j = 1; j <= n; j++) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j -1]) + grid[i - 1][j - 1];
}
}
// 4, 返回值
return dp[m][n];
}
五、地下城游戏(较难)
1, 题目
OJ链接
题目分析: 和上一题的行走方式一致, 本题要求至少有多少血才能走到右下角
需注意 : 原表中的值为负, 说明走到此位置会扣血, 如果原表中的值为正, 走到此位置会加血, 走到任意位置都要保证至少有 1 滴血即可,包括走到右下角时
比如当前有 5 滴血, 但下一步要扣 5(或 6) 滴血, 那么到下一步时, 没血了就死了
2, 思路分析
2.1, 状态表示
仍然使用划分子问题思想
但如果和之前的题一样, 以某位置为结尾考虑, 先求出从起点到达任意位置的路径总数, 这样无法推导出状态转移方程, 因为在某位置时, 会受到后面位置的影响(
本题中, 如果以某一位置为结尾, 求出至少需要的血量, 那你怎么知道会不会有某个位置要扣 999 滴血? 是无法预知的, 这种情况称为 “有后效性”
我们换个方向思考, 尝试以某一位置为起点, 需要多少血才能到达终点
画图
状态表示 : dp[i][j] 表示以 [i][j] 位置为起点, 到达终点需要的最少血量
如果 dp[i][j] 的值为 5, 在本题中就可以理解为, 在 [i][j] 位置时, 有 5 滴血就能走到终点
2.2, 状态转移方程
以 [i][j] 位置状态的最近的⼀步,来分情况讨论
从某个位置( [i][j] )为起点出发, 有两种情况
-
如果 : 当前位置
( [i][j] )--> 向右走( [i][j + 1] ) -
如果 : 当前位置
( [i][j] )--> 向下走( [i + 1][j] )
以第一种情况为例 : 根据状态表示可知, dp[i][j + 1] 表示有 dp[i][j + 1] 滴血就能走到终点, 如何求出 dp[i][j] ?
所以 X >= dp[i][j + 1] - 原表中当前位置的值 就能走到终点, 要求最小血量, 取等号即可
所以状态转移方程 : dp[i][j] = (dp[i][j + 1] , dp[i + 1][j]) 取最小值 + 原表中当前位置的值, 填表后一定要判断dp[i][j] <= 0 的情况 ! !
2.3, 初始化
初始化是为了填表的时候不越界访问
-
给出虚拟位置 , 由于dp[i][j] 依赖右边和下边的值, 建表的时候在最下面多建一行, 最右边多建一列
-
经过分析, 每次都要取最小值, 虚拟位置的值不应该干扰填表, 所以虚拟位置的值应该填为
Integer.MAX_VALUE, -
并且走到原表右下角之后还应该保证至少有 1 滴血, 所以最后一行和最后一列的倒数第二个位置应该填为 1
使用添加虚拟位置辅助初始化的方式, 一定要注意和原表中的下标映射关系!!
2.4, 填表顺序
由于dp[i][j] 依赖下面和右面值, 所以填表顺序是从下往上, 从右往左
和之前的题都不一样!!
2.5, 返回值
要求一开始至少有多少血才能走到终点, 应该返回 dp[0][0]
3, 代码
public int calculateMinimumHP(int[][] dungeon) {
// 1, 构建dp表
int m = dungeon.length;
int n = dungeon[0].length;
int[][] dp = new int[m + 1][n + 1];
// 2, 初始化
for(int i = 0; i <= m; i++) {
dp[i][n] = Integer.MAX_VALUE;
}
for(int i = 0; i <= n; i++){
dp[m][i] = Integer.MAX_VALUE;
}
dp[m - 1][n] = 1;
dp[m][n -1 ] = 1;
// 3, 填表
for(int i = m - 1; i >= 0; i--) {
for(int j = n - 1; j >= 0; j--) {
dp[i][j] = Math.min(dp[i][j + 1], dp[i + 1][j]) - dungeon[i][j];
dp[i][j] = Math.max(dp[i][j], 1);
}
}
// 4, 返回值
return dp[0][0];
}