论文《Cross-Session Aware Temporal Convolututional Network for Session-based Recommendation》阅读

论文概况

本文是美团发表在ICDM（CCF B会）的一个wrokshop上的一篇论文，聚焦于序列化推荐（sequential recommendation，或session-based recommendation（SBR））问题，提出了模型CA-TCN，如果没有问题的话，应该是最早使用全局图解决序列化推荐的模型。

Introduction

作者提出了几个问题：

• 现有模型没有考虑使用其他session信息来加强session内表示，造成了性能缺失
• 当前SBR流行的GNN方法存在缺陷，即GNN缺少了序列的位置信息，不同的序列构造完很可能是一幅图，例如$v_1\to v_2\to v_1\to v_3\to v_2\to v_4$序列和$v_1\to v_3\to v_2\to v_1\to v_2\to v_4$ 两个序列，都可以构造成如图1所示的图
• GNN存在过度平滑问题，众所周知，GNN最深一般3、 4层，即最多能够描述长度为3到4的序列，这与我们的主观认识是不相符的。我们平常购物中，经常有之前买了一件衣服，过很长时间需要搭配一条裤子，这之间可能有过数十次购买经历，但是这两者却是紧密相关的。

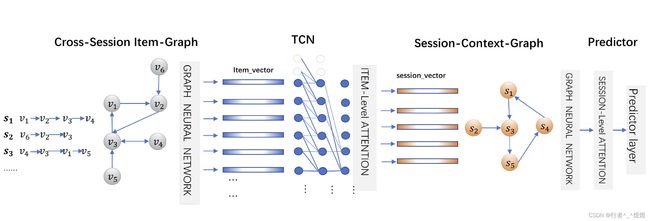
对于上述几点，作者通过 1）使用时间卷积网络（Temporal Convolutional Network，TCN）完成序列学习，这可以保证长序列的因果关系；2）使用item-level来表征全局物品属性，即显示同一个物品在不同session中对不同用户的吸引（如一个人买苹果耳机可能是因为喜欢苹果这个品牌，也可能是单纯喜欢各种耳机）；3）使用session-level来表征行为模式，即通过一个session来比较当前用户的一种行为模式，从而可以推测出不同模式之间的相似或不同。

Method

A. Cross-Session Item Graph

构造全局的cross-session图$G_{item}$，这里作者使用所有的session中的临边加入到一个总图中（即凡是有邻接的都接一遍）形成一个有向图，权重使用连接次数进行归一化。从而可以形成$A_{in}$和$A_{out}$用来表示入度、出度，并对应两个可训练矩阵$W_{in}$和$W_{out}$。最终形成所有物品的矩阵表示$V\in {\mathbb{R}}^{|V|\times dim}$，GNN迭代过程如下：
$$V^{l+1}=\sigma (D^{-1}(W_{in}{V}^l+W_{out}{V}^l+V^l)W^l)\text{\hspace{1em}(1)}$$

上式中，$D$表示$A_{in}$和$A_{out}$得出的度对角矩阵，$W^l$表示可训练矩阵，$\sigma (\cdot )$ 表示激活函数。

这里，使用两个矩阵$W_{in}$和$W_{out}$显得有点多余，用一个矩阵就可以了

另外，这里对公式进行了一定修改，矩阵$W_{in}$和$W_{out}$ 分别表示两个可训练矩阵，$V\in {\mathbb{R}}^{|V|\times dim}$使用$|V|$来表示维度，与前文保持一致，原文使用$m$与后文产生了冲突。

B.Temporal Convolutional Neural Network

这一部分使用前面GNN得出的物品embedding，传入TCN进行卷积。具体的，针对序列$s=\{v_{s,1},v_{s,2},\cdots ,v_{s,n}\}$，每个物品的向量使用GNN从$G_{item}$得到的全局embedding，即$[{\mathbf{v}}_{s,1},{\mathbf{v}}_{s,2},\cdots ,{\mathbf{v}}_{s,n}]$，传入TCN，对会话$s$中的每个物品向量${\mathbf{v}}_{s,i}$进行卷积操作$F$：
$$F({\mathbf{v}}_{s,i})=({\mathbf{v}}_{s,i}{\ast }_{d}f)=\sum _{j=0}^{k-1}f(j)\cdot {\mathbf{v}}_{s,i-d\cdot j}\text{\hspace{1em}(2)}$$

这里，对TCN具体内部操作没有过多了解，作者表示TCN感受野与神经网络层数呈指数关系，感受野内的节点等同于直接相连。

作者使用session序列最后一个TCN输出$s^{local}$作为local表示，即
$$s^{local}=F({\mathbf{v}}_{s,n})\text{\hspace{1em}(3)}$$

使用session内所有向量加权表示$s^{global}$得到global表示，即
$$s^{global}=\sum _{i=1}^n{\alpha }_{s,i}\cdot F({\mathbf{v}}_{s,i})\text{\hspace{1em}(4)}$$

其中，注意力权重${\alpha }_{s,i}$通过当前物品${\mathbf{v}}_{s,i}$与session最后一个物品${\mathbf{v}}_{s,n}$计算得到，这里应该是为了计算不同位置物品针对session（如$s^{local}$所示，最后一个物品表示session）的影响力，具体如下：

$${\alpha }_{s,i}=softmax(\sigma ({\mathbf{W}}_{1}F({\mathbf{v}}_{s,n})+{\mathbf{W}}_{2}F({\mathbf{v}}_{s,i})))\text{\hspace{1em}(5)}$$

C. Session-Context Graph

作者在这里构造了一个图$G_{session}$，使用时间顺序上每个session前的$m$个session作为候选，对$m$个session的global向量进行KNN计算得到相似度的前$K$个进行连接，得到所有session连接图，使用GAT计算不同session之间的权重系数，得到最终session的全局session表示如下所示：
$${\mathbf{s}}^{cross}=\sum _{t\in N_s}{\beta }_{s,t}{\mathbf{t}}^{global}$$

这里对公式进行了一定修改，以方便理解，这里的下标 $i$ 表示session编号，$N_s$表示$G_{session}$中当前session节点$s$的邻居节点，${\beta }_{s,t}$表示注意力系数，如原文公式(6)所示，这里从略。

D. Recommendation Decoder

session表示使用前面得到的所有向量加和，即
$$f=\sigma ({\mathbf{W}}_l{\mathbf{s}}^{local}+{\mathbf{W}}_g{\mathbf{s}}^{global}+{\mathbf{W}}_s{\mathbf{s}}^{cross})$$

$${\mathbf{s}}_{final}=f\cdot [{\mathbf{s}}^{local}\Vert {\mathbf{s}}^{global}]+(1-f){\mathbf{s}}^{cross}\text{\hspace{1em}(10)}$$

• 这里，${\mathbf{W}}_l$、${\mathbf{W}}_s$、${\mathbf{W}}_g$是三个变维矩阵，得到的不应该是一个向量吗？怎么变成实数了？？？数学表达有问题啊这里

• 另外得到实数$f$对$[{\mathbf{s}}^{local}\Vert {\mathbf{s}}^{global}]$和${\mathbf{s}}^{cross}$进行相加，俩向量维度应该是一样的啊，此处明显不对

• $f$应该是为了对两者进行平均，为什么这么操作作者也没有进行说明

得到最终的${\mathbf{s}}_{final}$，与每个物品$i$的embedding进行内积并使用softmax进行归一化得到结果，使用交叉熵作为损失函数进行训练。如下所示：

$${\hat{y}}_i=softmax({\mathbf{s}}_{final}^{\mathsf{T}}{\mathbf{v}}_i)$$

总结一下

• 这篇文章使用TCN达到了长期依赖的描述
• 应该是第一个考虑不同session之间相互作用的作品

一点不成熟的意见

• 文中数学表达较为混乱，需要仔细对比和推敲
• 文中cross session概念较为浅显，一方面构造了一个会话图 $G_{session}$ 作为session之间互相影响的证明，但是构造方面有点过于简单；另一方面构造了一个物品图 $G_{item}$ 用于描述物品在不同session之间的综合属性。但是从直觉上，本人认为使用TCN和GNN得到的embedding应该彼此分离，并在最终预测阶段进行拼接，效果应该会更好。理由如下：通过 $G_{item}$ 得到的物品embedding追求不同session之间物品的公有属性；而通过TCN得到的内部物品embedding则应该追求session自己的独特属性。