生成式AI系列——什么是生成对抗模型（GAN）？

1 如何通俗理解GAN？

​ 生成对抗网络(GAN, Generative adversarial network)自从2014年被Ian Goodfellow提出以来，掀起来了一股研究热潮。GAN由生成器和判别器组成，生成器负责生成样本，判别器负责判断生成器生成的样本是否为真。生成器要尽可能迷惑判别器，而判别器要尽可能区分生成器生成的样本和真实样本。

​ 在GAN的原作[1]中，作者将生成器比喻为印假钞票的犯罪分子，判别器则类比为警察。犯罪分子努力让钞票看起来逼真，警察则不断提升对于假钞的辨识能力。二者互相博弈，随着时间的进行，都会越来越强。那么类比于图像生成任务，生成器不断生成尽可能逼真的假图像。判别器则判断图像是否是真实的图像，还是生成的图像，二者不断博弈优化。最终生成器生成的图像使得判别器完全无法判别真假。

2 GAN的形式化表达

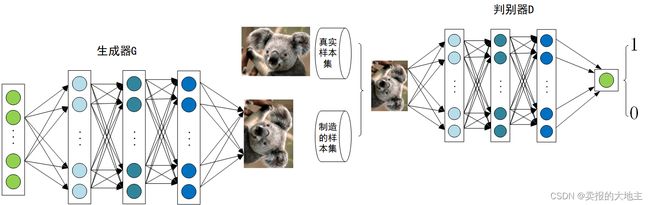
​ 上述例子只是简要介绍了一下GAN的思想，下面对于GAN做一个形式化的，更加具体的定义。通常情况下，无论是生成器还是判别器，我们都可以用神经网络来实现。那么，我们可以把通俗化的定义用下面这个模型来表示：

​ 上述模型左边是生成器G，其输入是$z$，对于原始的GAN，$z$是由高斯分布随机采样得到的噪声。噪声$z$通过生成器得到了生成的假样本。

​ 生成的假样本与真实样本放到一起，被随机抽取送入到判别器D，由判别器去区分输入的样本是生成的假样本还是真实的样本。整个过程简单明了，生成对抗网络中的“生成对抗”主要体现在生成器和判别器之间的对抗。

3 GAN的目标函数是什么？

​ 对于上述神经网络模型，如果想要学习其参数，首先需要一个目标函数。GAN的目标函数定义如下：

$$\underset{G}{\min }\underset{D}{\max }V(D,G)={\mathrm{E}}_{x\sim p_{data}(x)}[\log D(x)]+{\mathrm{E}}_{z\sim p_z(z)}[\log (1-D(G(z)))]$$
​ 这个目标函数可以分为两个部分来理解：

​ 第一部分：判别器的优化通过$\underset{D}{\max }V(D,G)$实现，$V(D,G)$为判别器的目标函数，其第一项${\mathrm{E}}_{x\sim p_{data}(x)}[\log D(x)]$表示对于从真实数据分布 中采用的样本 ,其被判别器判定为真实样本概率的数学期望。对于真实数据分布 中采样的样本，其预测为正样本的概率当然是越接近1越好。因此希望最大化这一项。第二项${\mathrm{E}}_{z\sim p_z(z)}[\log (1-D(G(z)))]$表示：对于从噪声$P_z(z)$分布当中采样得到的样本，经过生成器生成之后得到的生成图片，然后送入判别器，其预测概率的负对数的期望，这个值自然是越大越好，这个值越大， 越接近0，也就代表判别器越好。

​ 第二部分：生成器的优化通过$\underset{G}{\min }(\underset{D}{\max }V(D,G))$来实现。注意，生成器的目标不是$\underset{G}{\min }V(D,G)$，即生成器不是最小化判别器的目标函数，二是最小化判别器目标函数的最大值，判别器目标函数的最大值代表的是真实数据分布与生成数据分布的JS散度(详情可以参阅附录的推导)，JS散度可以度量分布的相似性，两个分布越接近，JS散度越小。

4 GAN的目标函数和交叉熵有什么区别？

​ 判别器目标函数写成离散形式即为:
$$V(D,G)=-\frac{1}{m}\sum _{i=1}^{i=m}logD(x^i)-\frac{1}{m}\sum _{i=1}^{i=m}log(1-D({\tilde{x}}^i))$$

​ 可以看出，这个目标函数和交叉熵是一致的，即判别器的目标是最小化交叉熵损失，生成器的目标是最小化生成数据分布和真实数据分布的JS散度。

---

[1]: Goodfellow, Ian, et al. “Generative adversarial nets.” Advances in neural information processing systems. 2014.

5 GAN的Loss为什么降不下去？

​ 对于很多GAN的初学者在实践过程中可能会纳闷，为什么GAN的Loss一直降不下去。GAN到底什么时候才算收敛？其实，作为一个训练良好的GAN，其Loss就是降不下去的。衡量GAN是否训练好了，只能由人肉眼去看生成的图片质量是否好。不过，对于没有一个很好的评价是否收敛指标的问题，也有许多学者做了一些研究，后文提及的WGAN就提出了一种新的Loss设计方式，较好的解决了难以判断收敛性的问题。下面我们分析一下GAN的Loss为什么降不下去？
​ 对于判别器而言，GAN的Loss如下：
$$\underset{G}{\min }\underset{D}{\max }V(D,G)={\mathrm{E}}_{x\sim p_{data}(x)}[\log D(x)]+{\mathrm{E}}_{z\sim p_z(z)}[\log (1-D(G(z)))]$$
​ 从$\underset{G}{\min }\underset{D}{\max }V(D,G)$可以看出，生成器和判别器的目的相反，也就是说两个生成器网络和判别器网络互为对抗，此消彼长。不可能Loss一直降到一个收敛的状态。

• 对于生成器，其Loss下降快，很有可能是判别器太弱，导致生成器很轻易的就"愚弄"了判别器。
• 对于判别器，其Loss下降快，意味着判别器很强，判别器很强则说明生成器生成的图像不够逼真，才使得判别器轻易判别，导致Loss下降很快。

​ 也就是说，无论是判别器，还是生成器。loss的高低不能代表生成器的好坏。一个好的GAN网络，其GAN Loss往往是不断波动的。

​ 看到这里可能有点让人绝望，似乎判断模型是否收敛就只能看生成的图像质量了。实际上，后文探讨的WGAN，提出了一种新的loss度量方式，让我们可以通过一定的手段来判断模型是否收敛。

6 生成式模型、判别式模型的区别？

​ 对于机器学习模型，我们可以根据模型对数据的建模方式将模型分为两大类，生成式模型和判别式模型。如果我们要训练一个关于猫狗分类的模型，对于判别式模型，只需要学习二者差异即可。比如说猫的体型会比狗小一点。而生成式模型则不一样，需要学习猫长什么样，狗长什么样。有了二者的长相以后，再根据长相去区分。具体而言：

• 生成式模型：由数据学习联合概率分布P(X,Y), 然后由P(Y|X)=P(X,Y)/P(X)求出概率分布P(Y|X)作为预测的模型。该方法表示了给定输入X与产生输出Y的生成关系

• 判别式模型：由数据直接学习决策函数Y=f(X)或条件概率分布P(Y|X)作为预测模型，即判别模型。判别方法关心的是对于给定的输入X，应该预测什么样的输出Y。

​ 对于上述两种模型，从文字上理解起来似乎不太直观。我们举个例子来阐述一下，对于性别分类问题，分别用不同的模型来做：

​ 1）如果用生成式模型：可以训练一个模型，学习输入人的特征X和性别Y的关系。比如现在有下面一批数据：

Y（性别）		0	1
X（特征）	0	1/4	3/4
	1	3/4	1/4

​ 这个数据可以统计得到，即统计人的特征X=0,1….的时候，其类别为Y=0,1的概率。统计得到上述联合概率分布P(X, Y)后，可以学习一个模型，比如让二维高斯分布去拟合上述数据，这样就学习到了X，Y的联合分布。在预测时，如果我们希望给一个输入特征X，预测其类别，则需要通过贝叶斯公式得到条件概率分布才能进行推断：
$$P(Y|X)=\frac{P(X,Y)}{P(X)}=\frac{P(X,Y)}{P(X|Y)P(Y)}$$
​ 2）如果用判别式模型：可以训练一个模型，输入人的特征X，这些特征包括人的五官，穿衣风格，发型等。输出则是对于性别的判断概率，这个概率服从一个分布，分布的取值只有两个，要么男，要么女，记这个分布为Y。这个过程学习了一个条件概率分布P(Y|X)，即输入特征X的分布已知条件下，Y的概率分布。

​ 显然，从上面的分析可以看出。判别式模型似乎要方便很多，因为生成式模型要学习一个X，Y的联合分布往往需要很多数据，而判别式模型需要的数据则相对少，因为判别式模型更关注输入特征的差异性。不过生成式既然使用了更多数据来生成联合分布，自然也能够提供更多的信息，现在有一个样本（X,Y）,其联合概率P（X,Y）经过计算特别小，那么可以认为这个样本是异常样本。这种模型可以用来做outlier detection。

7 什么是mode collapsing?

​ 某个模式(mode)出现大量重复样本，例如：

​ 上图左侧的蓝色五角星表示真实样本空间，黄色的是生成的。生成样本缺乏多样性，存在大量重复。比如上图右侧中，红框里面人物反复出现。

8 如何解决mode collapsing？

方法一：针对目标函数的改进方法

​ 为了避免前面提到的由于优化maxmin导致mode跳来跳去的问题，UnrolledGAN采用修改生成器loss来解决。具体而言，UnrolledGAN在更新生成器时更新k次生成器，参考的Loss不是某一次的loss，是判别器后面k次迭代的loss。注意，判别器后面k次迭代不更新自己的参数，只计算loss用于更新生成器。这种方式使得生成器考虑到了后面k次判别器的变化情况，避免在不同mode之间切换导致的模式崩溃问题。此处务必和迭代k次生成器，然后迭代1次判别器区分开[8]。DRAGAN则引入博弈论中的无后悔算法，改造其loss以解决mode collapse问题[9]。前文所述的EBGAN则是加入VAE的重构误差以解决mode collapse。

方法二：针对网络结构的改进方法

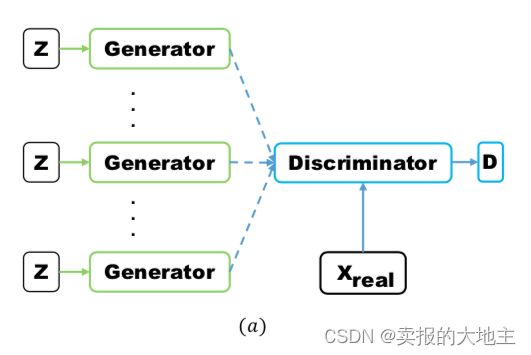
​ Multi agent diverse GAN(MAD-GAN)采用多个生成器，一个判别器以保障样本生成的多样性。具体结构如下：

​ 相比于普通GAN，多了几个生成器，且在loss设计的时候，加入一个正则项。正则项使用余弦距离惩罚三个生成器生成样本的一致性。

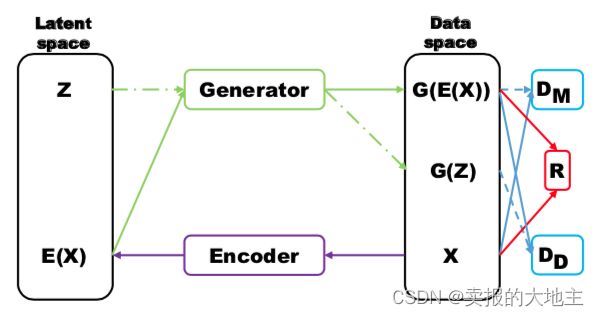
​ MRGAN则添加了一个判别器来惩罚生成样本的mode collapse问题。具体结构如下：

​ 输入样本$x$通过一个Encoder编码为隐变量$E(x)$，然后隐变量被Generator重构，训练时，Loss有三个。$D_M$和$R$（重构误差）用于指导生成real-like的样本。而$D_D$则对$E(x)$和$z$生成的样本进行判别，显然二者生成样本都是fake samples，所以这个判别器主要用于判断生成的样本是否具有多样性，即是否出现mode collapse。

方法三：Mini-batch Discrimination

​ Mini-batch discrimination在判别器的中间层建立一个mini-batch layer用于计算基于L1距离的样本统计量，通过建立该统计量，实现了一个batch内某个样本与其他样本有多接近。这个信息可以被判别器利用到，从而甄别出哪些缺乏多样性的样本。对生成器而言，则要试图生成具有多样性的样本。