SPSS--如何使用分层分析以及分层分析案例分享
分层分析:将资料按某个或某些需要控制的变量的不同分类进行分层,然后再估计暴露因子与某结局变量之间关系的一种资料分析方法。
分层分析的最重要的用途是评估和控制混杂因子所致的混杂偏倚。通过按混杂因子分层,可使每层内的两个比较组在所控制的混杂因子方面齐同,从而消除混杂作用;另一个重要用途是评估和描述效应修饰。另外,分层分析还可用于描述随访研究中的失访问题和竞争风险、研究两因子之间的生物学交互作用、以及生存分析和诱导期分析。
1.基本步骤概述
① 分层列表
将资料按混杂因子分层后,然后分别计算各层的效应估计值。
② 检验层别效应估计值
在绝大多数分层分析中,效应估计值在各层都有一些变化,而这些变化的意义却不尽相同。有些是随机变异的结果,有些是各种偏倚所致的,而有些却是极其重要的需要揭示的结果(如效用修饰或交互作用)。因此,在计算出各层的效应估计值后,应对其进行检验与分析,以明确层别效应估计值的变化有无统计学意义和重要的流行病学意义。明确这些问题对决定下一步用什么分析方法和如何报告分层分析的结果将起关键作用。因此,层别效应估计值的检验是至关重要的。然面,这一步骤并非总是可行的。有些变量可能因为种类太多而无法计算每层的效应估计值。如要研究家庭所致的潜在混杂作用,则因每个家庭的受试者太少而不能从每一个家庭计算出一个稳定的和可信的效应估计值。
3.层别效应的一致性假设与检验
绝大多数的分层分析方法是以各层效应大小一致( 即同质的)为基础的。即要求各层的效应估计值相等。在这种情况下,这些层别估计值就能够通过方差的倒数加权而有效地被平均,计算出一个合并估计值。因此,在分层分析中一般均假设层别效应是一致的。然而,即使各层的效应大小是一致的,通过抽样研究得来的资料其层别效应估计值多少会有差异。因此,关键是要判断层别效应估计值的变化程度与一致性效应的可能随机变异是否一致。那么如何判断这种一致性假 设是否正确呢?简单的办法是只要致性假设与资料或其他证据不明显矛盾,则可认为是合理的。然而这种推测有太大的主观性,调查者一般更希望对这种假设的正确性有一个正式的统计学显著性检验。
层别效应一致性的假设检验即 为同质性检验( homogeneity test)(即假设在各层有一个恒定的效应估计值) ,它是以一致效应的总估计值与层别效应估计值的比较为基础的,即在同质性假设条件下,期望数与实际观察数的比较。因此,在作同质性检验时,先要在同质性假设条件下,求出一个一致效应的总估计值,然后与各层别估计值比较。
由于比值测量的一致性通常意味着差异测量的异质性,而差异测量的致性也同样意味着比值测量的异质性。因此,对比值和差异测量的一致性需要单独评价。
4. 调整控制混杂
如果同质性检验结果证明层别效应是致的,分层分析则以调整控制混杂为主。其计算主要包括一致效应的合并点估计区间估计及统计检验的P值。依据资料类型所用的效应测量指标、样本大小及要求精确度高低的不同,有不同的计算方法。
5.评价和描述效用修饰
如果同质性检验的结果拒绝了检验假设,即层间效应估计值的差异有统计学意义时,则认为该变量具有效用修饰作用。此时,分层分析的目标指向效用修饰的评价与描述。
具体步骤与方法
案例分析
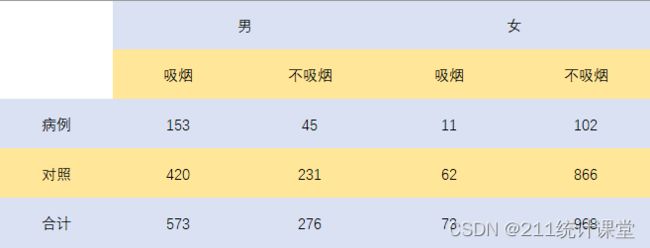
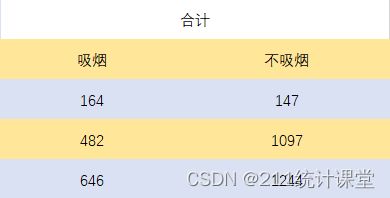
在某项关于吸烟与胃癌关系的病例对照研究中,采用分层分析探讨性别的可能混杂作用,数据整理后如下图所示。
【SPSS】
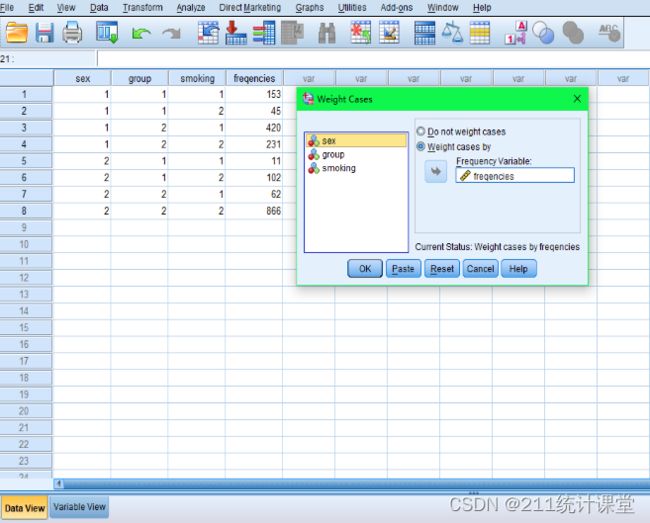
(Ⅰ):频数加权,对变量“freqencies”作加权处理
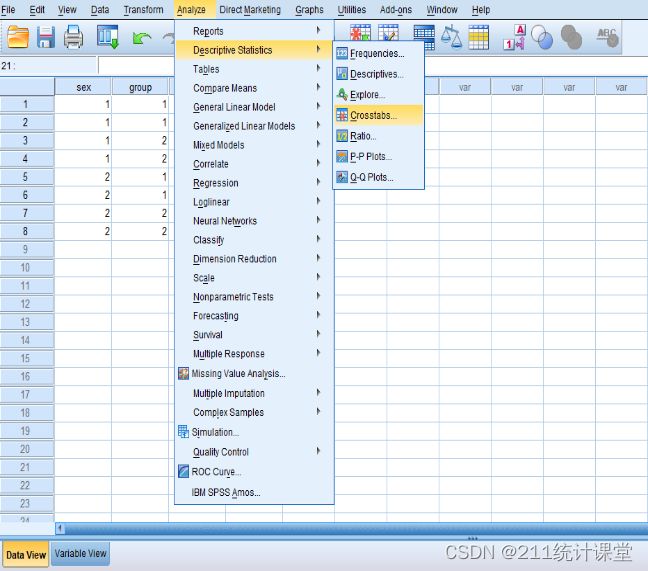
(Ⅱ):analyze→descriptive statisics→crosstabs
弹出如下所示对话框
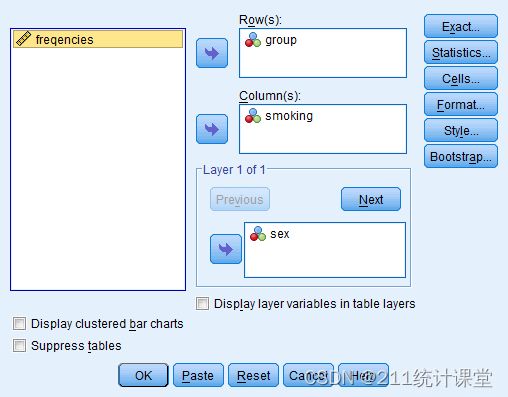
(Ⅲ):将变量group(病例组与对照组)选入row,smoking选入column,sex选入layer(层)
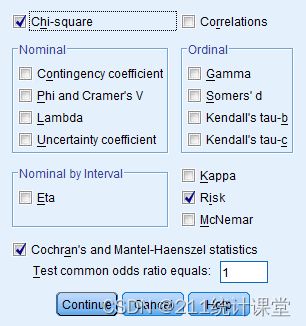
(Ⅳ):单击Statistics(统计量),勾选Chi-square,Risk(OR),以及
Cochran's and Mantel-Haenszel statistics
结果解析
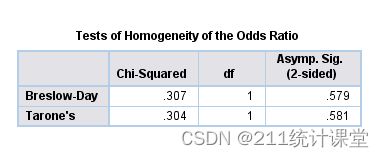
(Ⅰ)
同质性检验:chi-square=0.31,P=0.58 ,各层比值比一致。也即,在不同性别中,吸烟与胃癌的发生是相同的。
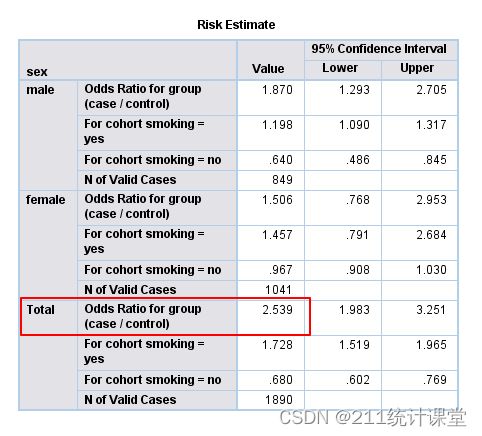
(Ⅱ)该资料显示:male:OR=1.87female:OR=1.506不考虑性别:OR=2.539
分层前后,OR值出现不等,即性别起了一定混杂作用。
(Ⅲ)
调整后的Estimate为1.792,结合粗OR(2.539),即吸烟与肺癌的研究中,性别有一定的混杂作用。