zjuoj 3608 Signal Detection

http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3608

 

Signal Detection

---

Time Limit: 2 Seconds       Memory Limit: 65536 KB

---

Parallelepiped
Type	Prism
Faces	6 parallelograms
Edges	12
Vertices	8

Dr. Gale is testing his laser system. He uses a detector to collect the signals from a laser generator. He also puts a special prism in the system so that he can filter the noise. But he is not very sure where to put the detector to collect the signals. Can you help him with this problem?

 

 

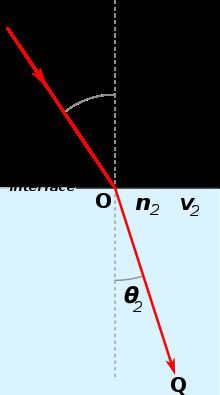
In order to simplify the problem, here we assume the prism is a parallelepiped, which is a three-dimensional figure formed by six parallelograms. The laser goes in one direction and the detector can receive signals from any direction. The detector is placed on the ground where the z-coordinate is zero. There is no energy lost in the refraction. That is to say, there is no reflection in the signal transmission. You don't need to consider the situation of total reflection or the degenerate situation.

Input

There are multiple test cases. The first line of input contains an integer T (T ≤ 50) indicating the number of test cases. Then T test cases follow.

The first line of each test case contains 3 integers, indicating the coordinates of the laser generator. The second line contains 3 integers describing a point the laser will go through without the prism. The third line contains 3 integers describing a vertex A of the prism. The fourth to the sixth lines contain 3 integers each, describing an adjacent vertex of A. The seventh line contains a real number u, the refractive index of the prism.(1 < u ≤ 10) The absolute value of the coordinates will not exceed 1000. The z coordinates are all nonnegative. The prism and the laser generator are strictly above the ground and the laser generator will not be inside the prism.

Output

If there is no place in the ground that can receive the signals output "Error". Otherwise, output the x and y coordinates the place accurate to 0.001.

Sample Input

2

0 0 10

0 0 0

-5 -5 1

5 -5 11

-5 5 1

-6 -5 2

1.4142136

0 0 10

0 0 11

-5 -5 1

5 -5 1

-5 5 1

-5 -5 2

2

Sample Output

0.423 0.000

Error

References

• http://en.wikipedia.org/wiki/Parallelepiped

---

Author: GUAN, Yao
Contest: The 9th Zhejiang Provincial Collegiate Programming Contest

 

 

AC代码：

 

  1 #include <cstdlib>

  2 #include <cstdio>

  3 #include <cstring>

  4 #include <cmath>

  5 #include <iostream>

  6 #include <algorithm>

  7 #include <string>

  8 #include <vector>

  9 #include <set>

 10 #include <map>

 11 #include <queue>

 12 #include <time.h>

 13 using namespace std;

 14 typedef long long llong;

 15 

 16 inline int bit(int x, int i){ return (x>>i) & 1;}

 17 inline int setb(int x, int i){ return x | (1 << i);}

 18 inline int clrb(int x, int i){ return x & (~(1 << i));}

 19 inline int lowb(int x){return x & (-x);}

 20 const double eps = 1e-9;

 21 struct Point{

 22     double x, y, z;

 23     Point(){}

 24     Point(double x, double y, double z):x(x), y(y), z(z){}

 25     double len(){

 26         return sqrt(x * x + y * y + z * z);

 27     }

 28     Point shrink(double l = 1.0){

 29         double s = l / len();

 30         return Point(x * s, y * s, z * s);

 31     }

 32     void input(){

 33         scanf("%lf %lf %lf", &x, &y, &z);

 34     }

 35 };

 36 

 37 Point operator +(const Point &p, const Point &q){

 38     return Point(p.x + q.x, p.y + q.y, p.z + q.z);

 39 }

 40 Point operator -(const Point &p, const Point &q){

 41     return Point(p.x - q.x, p.y - q.y, p.z - q.z);

 42 }

 43 Point operator *(const Point &p, const double &s){

 44     return Point(p.x * s, p.y * s, p.z * s);

 45 }

 46 Point operator *(const Point &p, const Point &q){

 47     return Point(p.y * q.z - p.z * q.y,

 48                  p.z * q.x - p.x * q.z,

 49                  p.x * q.y - p.y * q.x);

 50 }

 51 double operator &(const Point &p, const Point &q){

 52     return p.x * q.x + p.y * q.y + p.z * q.z;

 53 }

 54 

 55 Point p, q, v[8];

 56 double r;

 57 int face[][4] ={

 58 {3, 2, 1, 0},

 59 {4, 5, 6, 7},

 60 {0, 1, 5, 4},

 61 {2, 3, 7, 6},

 62 {1, 2, 6, 5},

 63 {0, 4, 7, 3},

 64 };

 65 Point fn[6];

 66 double fb[6];

 67 

 68 double inter(const Point &p, const Point &d, const Point &n, double b){

 69     return (b - (n & p)) / (n & d);

 70 }

 71 bool collide(double R){

 72     int hf = -1;

 73     double ht;

 74     Point d = (q - p);

 75     for(int i = 0;i < 6; ++i){

 76         if(fabs(fn[i] & d) < eps) continue;

 77         double t = inter(p, d, fn[i], fb[i]);

 78         if(t <= eps) continue;

 79         Point hit = p + d * t;

 80         bool ok = true;

 81         for(int j = 0;j < 4; ++j){

 82             if((((v[face[i][j]]-hit) * (v[face[i][(j + 1)%4]] - hit)) & fn[i]) <= 0) ok = false;

 83         }

 84         if(ok && (hf < 0 || t < ht)){

 85             hf = i;

 86             ht = t;

 87         }

 88     }

 89     if(hf < 0) return false;

 90     

 91     Point hit = p + d * ht;

 92     Point vx = fn[hf].shrink();

 93     if(fabs((vx * d).len()) < eps){

 94         p = hit;

 95         q = hit + d;

 96         return true;

 97     }

 98     double dx = vx & d;

 99     if(dx < 0) vx = vx * -1, dx = -dx;

100     Point vy = ((vx * d) * vx).shrink();

101     double dy = vy & d;

102     if(dy < 0) vy = vy * -1, dy = -dy;

103     double theta0 = atan2(dy, dx);

104     double theta = asin(sin(theta0) / R);

105     d = vx * cos(theta) + vy * sin(theta);

106     p = hit;

107     q = hit + d;

108     return true;

109 }

110 int main(){

111     int TT;

112     scanf("%d", &TT);

113     for(int cas = 1; cas <= TT; ++cas){

114         p.input();

115         q.input();

116         

117         v[0].input();

118         v[1].input();

119         v[3].input();

120         v[2] = v[1] + v[3] - v[0];

121         

122         v[4].input();

123         v[5] = v[4] + v[1] - v[0];

124         v[6] = v[4] + v[2] - v[0];

125         v[7] = v[4] + v[3] - v[0];

126         

127         scanf("%lf", &r);

128         for(int i = 0;i < 6; ++i){

129             fn[i] = (v[face[i][1]] - v[face[i][0]]) *

130                     (v[face[i][3]] - v[face[i][0]]);

131             fb[i] = fn[i] & v[face[i][0]];

132         }

133         if(collide(r)){

134             collide(1./r);

135         }

136         Point norm(0, 0, 1);

137         Point dir = q - p;

138         if(fabs(norm & dir) < eps) puts("Error");

139         else{

140             double t = inter(p, dir, norm, 0);

141             if(t < 0) puts("Error");

142             else{

143                 Point hit = p + dir * t;

144                 printf("%.3f %.3f\n", hit.x, hit.y);

145             }

146         }

147     }

148     return 0;

149 }

View Code