基础论文学习（1）——ViT

Vision Transformer（ViT） 模型架构是在 ICLR 2021 上作为会议论文发表的一篇研究论文中介绍的，题为“An Image is Worth 16*16 Words: Transformers for Image Recognition at Scale”。它由Neil Houlsby，Alexey Dosovitskiy和Google研究大脑团队的另外10位作者开发和出版。 调整代码和预先训练的ViT模型可以在 谷歌研究团队的GitHub上找到。你可以在这里找到它们。ViT模型在ImageNet和ImageNet-21k数据集上进行了预训练。

在下文中，我们将重点介绍多年来开发的一些最重要的Vision Transformer。它们基于Transformer架构，该架构最初是在 2017 年为自然语言处理 （NLP） 提出的。

日期	模型	简述	Vision Transformer?
2017	Transformer	仅基于注意力机制的模型。它在NLP任务上表现出色。	不
2018	BERT	预先训练的变压器模型开始主导NLP领域。	不
2020	DETR	DETR是一个简单而有效的高级视觉框架，它将对象检测视为直接集合预测问题。	是的
2020	GPT-3	GPT-3 是具有 170B 参数的巨大变压器模型，向通用 NLP 模型迈出了重要的一步。	不
2020	iGPT	最初为 NLP 开发的转换器模型也可用于图像预训练。	是的
2020	ViT	对视觉识别有效的纯变压器架构。	是的
2020	IPT/SETR/CLIP	变压器已分别应用于低级视觉、分割和多模态任务。	是的
2021以后	ViT 变体	有几种 ViT 变体，包括 DeiT、PVT、TNT、Swin 和 CSWin （2022）。	是的

CNN和ViT之间的区别（ViT与CNN）

与卷积神经网络 （CNN） 相比，视觉转换器 （ViT） 取得了显著的结果，同时获得的用于预训练的计算资源要少得多。与卷积神经网络（CNN）相比，视觉转换器（ViT）显示出通常较弱的归纳偏差(inductive bias)，导致在较小的数据集上进行训练时对模型正则化或数据增强（AugReg）的依赖性增加。 ViT 是基于变压器架构的可视化模型，最初是为基于文本的任务而设计的。ViT 模型将输入图像表示为一系列图像补丁，就像使用转换器对文本使用的一系列词嵌入一样，并直接预测图像的类标签。当在足够的数据上进行训练时，ViT 表现出非凡的性能，以 4 倍的计算资源打破了类似最先进的 CNN 的性能。

CNN使用像素阵列，而ViT将输入图像拆分为视觉标记。可视转换器将图像划分为固定大小的图块，正确嵌入每个图块，并将位置嵌入作为转换器编码器的输入。此外，ViT模型在计算效率和准确性方面比CNN高出近四倍。 ViT 中的自我注意层使得在整个图像中全局嵌入信息成为可能。该模型还学习训练数据，以编码图像补丁的相对位置以重建图像的结构。

1. 视觉变压器 ViT 架构

文献中已经提出了几种视觉变压器模型。视觉转换器架构的整体结构包括以下步骤：

• Split an image into patches (fixed sizes)
• Flatten the image patches
• Create lower-dimensional linear embeddings from these flattened image patches
• Add positional embeddings
• Feed the sequence as an input to a state-of-the-art transformer encoder
• Pre-train the ViT model with image labels (fully supervised on a huge dataset)
• Fine-tune the downstream dataset for image classification

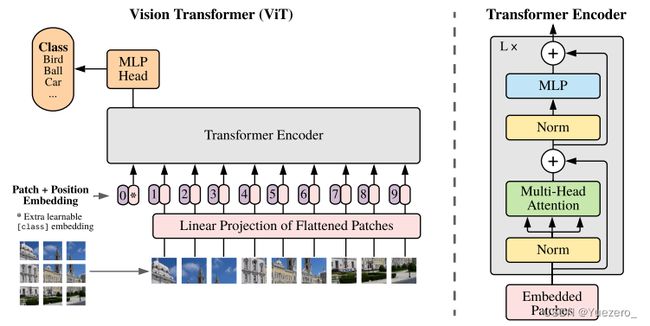
Vision Transformer（ViT）是一种使用self-attention来处理图像的架构。Vision Transformer架构由一系列变压器块组成。每个Transformer encoder模块由两个子层组成：Patch Embedding层、Multi-Head Self-Attention层、FeedForward层、MLP分类头。

Patch Embedding层，将图像划分为固定大小的Ptach，并将每个补丁映射(MLP)到高维矢量token表示。然后将这些tokens嵌入送入Transformer块进行进一步处理。

Multi-Head Self-Attention层根据图像中每个像素与所有其他像素的关系计算其注意力权重，多头注意力通过允许模型同时关注输入序列的不同部分来扩展此机制。而FeedForward层对自注意层的输出应用非线性变换。

ViT架构的最终输出是类预测，通过将最后一个Transformer模块的输出的CLS token，通过MLP分类头获得，分类头通常由单个全连接层组成。

唯一改变的是这些块的数量Layer。为此，为了进一步证明使用更多数据可以训练更大的ViT变体，提出了3个模型：

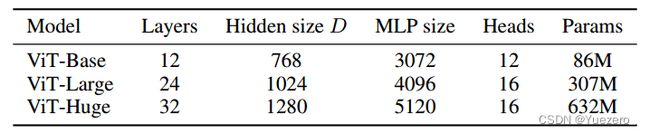
Layer就是encoder堆叠的层数，Heads是指多头注意力的头数，而MLP size是指多层感知器特征维度，但它实际上是一堆线性转换层，Hidden size D是embedding的token大小，在整个图层中保持固定。为什么要保持固定？这样我们就可以使用短的残差边跳跃连接。

ViT在大型数据集上进行预训练，然后微调为小数据集。唯一的修改是丢弃预测头（MLP 头）并附加一个新的D×K线性图层，其中 K 是小数据集的种类数。

1 图片分块和降维

因为transformer encoder的输入需要序列，所以最简单做法就是把图片切分为patch，然后拉成序列即可。 假设输入图片大小是256x256，打算分成64个patch，每个patch是32x32像素：

x = rearrange(img, 'b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1=p, p2=p)

这个写法是采用了爱因斯坦表达式，具体是采用了einops库实现，内部集成了各种算子，rearrange就是其中一个，非常高效。p就是patch大小，假设输入是[b,3,256,256]，则rearrange操作是先变成(b,3,8x32,8x32)，最后变成(b,8x8,32x32x3)即(b,64,3072)，将每张图片切分成64个小块，每个小块长度是32x32x3=3072，也就是说输入长度为64的图像序列，每个元素采用3072长度进行编码。

考虑到3072有点大，故作者先进行降维：

# 将3072变成dim，假设是1024
self.patch_to_embedding = nn.Linear(patch_dim, dim)
x = self.patch_to_embedding(x)

2 增加CLS token

仔细看论文上图，可以发现假设切成9个块，但是最终到transfomer输入是10个向量，额外追加了一个0和。为啥要追加？原因是我们现在没有解码器了，而是编码后直接就进行分类预测，那么该编码器就要负责一点点解码器功能，那就是：需要一个类似开启解码标志，非常类似于标准transformer解码器中输入的目标嵌入向量右移一位操作。试下如果没有额外输入，9个块输入9个编码向量输出，那么对于分类任务而言，我应该取哪个输出向量进行后续分类呢？选择任何一个都说不通，所以作者追加了一个可学习嵌入向量输入。那么额外的可学习嵌入向量为啥要设计为可学习，而不是类似nlp中采用固定的token代替？个人不负责任的猜测这应该就是图片领域和nlp领域的差别，nlp里面每个词其实都有具体含义，是离散的，但是图像领域没有这种真正意义上的离散token，有的只是一堆连续特征或者图像像素，如果不设置为可学习，那还真不知道应该设置为啥内容比较合适，全0和全1也说不通。 自此现在就是变成10个向量输出，输出也是10个编码向量，然后取第0个编码输出进行分类预测即可。从这个角度看可以认为编码器多了一点点解码器功能。具体做法超级简单，0就是位置编码向量，是可学习的patch嵌入向量。

# dim=1024
self.cls_token = nn.Parameter(torch.randn(1, 1, dim))
# 变成(b,64,1024)
cls_tokens = repeat(self.cls_token, '() n d -> b n d', b=b)
# 额外追加token，变成b,65,1024
x = torch.cat((cls_tokens, x), dim=1)

3 位置编码PE

1-D 位置编码：例如3x3共9个patch，patch编码为1到9

2-D 位置编码：patch编码为11,12,13,21,22,23,31,32,33，即同时考虑X和Y轴的信息，每个轴的编码维度是D/2

即使应用了许多位置嵌入方案，也没有发现显着差异。这可能是由于变压器编码器在patch级别工作。捕获patch（空间信息）之间的顺序关系的学习嵌入并不是那么重要。理解 P x P 的patch块之间的关系比完整图像H x W 之间的关系相对容易。

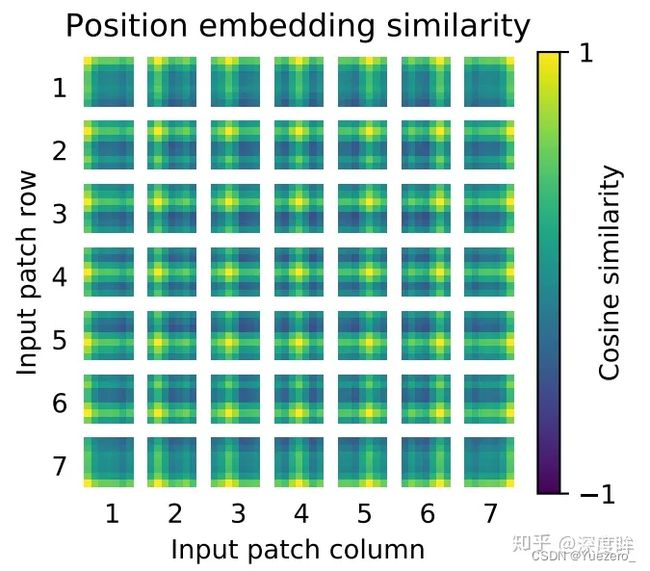
这里做的比较简单，没有采用sincos编码，而是直接设置为可学习，效果差不多。相邻位置有相近的位置编码向量，整体呈现2d空间位置排布一样。将patch嵌入向量和位置编码向量相加即可作为编码器输入:

# num_patches=64，dim=1024,+1是因为多了一个cls开启解码标志
self.pos_embedding = nn.Parameter(torch.randn(1, num_patches + 1, dim))
x += self.pos_embedding[:, :(n + 1)]
x = self.dropout(x)

对训练好的pos_embedding进行可视化，如下所示：

4 Transformer Encoder

作者采用的是没有任何改动的transformer，故没有啥说的。

self.transformer = Transformer(dim, depth, heads, mlp_dim, dropout)

假设输入是(b,65,1024)，那么transformer输出也是(b,65,1024)

5 分类head

在编码器后接fc分类器head即可

self.mlp_head = nn.Sequential(
            nn.LayerNorm(dim),
            nn.Linear(dim, mlp_dim),
            nn.GELU(),
            nn.Dropout(dropout),
            nn.Linear(mlp_dim, num_classes)
        )

# 65个输出里面只需要第0个输出进行后续分类即可
self.mlp_head(x[:, 0])

总体架构

到目前为止就全部写完了，是不是非常简单，外层整体流程为：

import torch
from torch import nn
from einops import rearrange, repeat
from einops.layers.torch import Rearrange

# helpers

def pair(t):
    return t if isinstance(t, tuple) else (t, t)

# classes

class FeedForward(nn.Module):  
	# LN + FC + GELU + Dropout + FC + Dropout
    def __init__(self, dim, hidden_dim, dropout = 0.):
        super().__init__()
        self.net = nn.Sequential(
            nn.LayerNorm(dim),
            nn.Linear(dim, hidden_dim),
            nn.GELU(),
            nn.Dropout(dropout),
            nn.Linear(hidden_dim, dim),
            nn.Dropout(dropout)
        )

    def forward(self, x):
        return self.net(x)
        

class Attention(nn.Module):
	# LN(x)  ->  qkv  ->  Softmax(q*k/dk)*v  ->  FC
    def __init__(self, dim, heads = 8, dim_head = 64, dropout = 0.):
        super().__init__()
        inner_dim = dim_head *  heads
        project_out = not (heads == 1 and dim_head == dim)

        self.heads = heads
        self.scale = dim_head ** -0.5

        self.norm = nn.LayerNorm(dim)

        self.attend = nn.Softmax(dim = -1)
        self.dropout = nn.Dropout(dropout)

        self.to_qkv = nn.Linear(dim, inner_dim * 3, bias = False)

        self.to_out = nn.Sequential(
            nn.Linear(inner_dim, dim),
            nn.Dropout(dropout)
        ) if project_out else nn.Identity()

    def forward(self, x):
        x = self.norm(x)

        qkv = self.to_qkv(x).chunk(3, dim = -1)
        q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h = self.heads), qkv)

        dots = torch.matmul(q, k.transpose(-1, -2)) * self.scale

        attn = self.attend(dots)
        attn = self.dropout(attn)

        out = torch.matmul(attn, v)
        out = rearrange(out, 'b h n d -> b n (h d)')
        return self.to_out(out)


class Transformer(nn.Module):
	# depth=12层Attention + FeedForward -> LN
    def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout = 0.):
        super().__init__()
        self.layers = nn.ModuleList([])
        for _ in range(depth):
            self.layers.append(nn.ModuleList([
                Attention(dim, heads = heads, dim_head = dim_head, dropout = dropout),
                FeedForward(dim, mlp_dim, dropout = dropout)
            ]))
            
		self.norm = nn.LayerNorm(dim)

    def forward(self, x):
        for attn, ff in self.layers:
            x = attn(x) + x
            x = ff(x) + x
        return self.norm(x)


class ViT(nn.Module):
	# to_patch_embedding + cat_cls_token + add_pos_embedding + transformer + mlp_head
    def __init__(self, *, image_size, patch_size, num_classes, dim, depth, heads, mlp_dim, pool = 'cls', channels = 3, dim_head = 64, dropout = 0., emb_dropout = 0.):
        super().__init__()
        image_height, image_width = pair(image_size)
        patch_height, patch_width = pair(patch_size)

        assert image_height % patch_height == 0 and image_width % patch_width == 0, 'Image dimensions must be divisible by the patch size.'

        num_patches = (image_height // patch_height) * (image_width // patch_width)
        patch_dim = channels * patch_height * patch_width
        assert pool in {'cls', 'mean'}, 'pool type must be either cls (cls token) or mean (mean pooling)'

        self.to_patch_embedding = nn.Sequential(
            Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1 = patch_height, p2 = patch_width),
            nn.LayerNorm(patch_dim),
            nn.Linear(patch_dim, dim),
            nn.LayerNorm(dim),
        )

        self.pos_embedding = nn.Parameter(torch.randn(1, num_patches + 1, dim))
        self.cls_token = nn.Parameter(torch.randn(1, 1, dim))
        self.dropout = nn.Dropout(emb_dropout)

        self.transformer = Transformer(dim, depth, heads, dim_head, mlp_dim, dropout)

        self.pool = pool
        self.to_latent = nn.Identity()  # 创建一个恒等映射层，用于不做任何改变地传递输入数据

        self.mlp_head = nn.Linear(dim, num_classes)

    def forward(self, img):
        x = self.to_patch_embedding(img)
        b, n, _ = x.shape

        cls_tokens = repeat(self.cls_token, '1 1 d -> b 1 d', b = b)
        x = torch.cat((cls_tokens, x), dim=1)
        x += self.pos_embedding[:, :(n + 1)]
        x = self.dropout(x)

        x = self.transformer(x)

        x = x.mean(dim = 1) if self.pool == 'mean' else x[:, 0]

        x = self.to_latent(x)
        return self.mlp_head(x)

2. 实验分析

作者得出的结论是：cv领域应用transformer需要大量数据进行预训练，在同等数据量的情况下性能不如cnn。一旦数据量上来了，对应的训练时间也会加长很多，那么就可以轻松超越cnn。