放大器增益的测量
增益是所有放大器的一个基本功能,它是放大器的输入信号与放大器的输出信号比值,大多数时候增益大于1,有时也会小于1。图11-1表明了如何测量一个放大器的电压增益。例如,如果输入信号为1v,输出信号为10v,那么增益为:
增益是一个无单位的纯数,说这个放大器的增益为10v是不对的。
例1
如果输出信号为4v,输入信号为50mv,计算这个放大器的增益。
![]()
例2
如果一个放大器的增益为50,当输入为20mv时,求它的输出信号的幅度。
公式变形为:
![]()
通常字母a用来标记增益或学中的放大倍数。加一个下标说明增益的类型:
![]()
电压增益
电流增益
![]()
功率增益
电压增益au用于描述小信号放大器的工作。功率增益ap通常来描述大信号放大器的工作。如果图11-1所示的放大器是一个功率放大器或大信号放大器,其增益基础是用瓦特而不是用伏特来计算的。例如,如果输入信号为0.5w,输出信号为8w,功率增益是:
![]()
例3
输出功率为1w,求功率增益为20的放大器的pin。公式变形:
电子学早期应用于通讯领域,大部分电路的有效输出是供给耳机或扬声器的声音。因此,工程师和技术人员设法使电路性能和人的听觉相一致。人耳对于声音的功率响应并不是线性的,它不能辨认出以线性变化的声音强弱。例如,如果你目前听到扬声器的输入为0.1w,当功率突然增加到1w,你会觉得声音突然变大了。那么假设功率再突然增加到10w,你也会注意到音量的增加。有趣的是,你可能会认为第二次变化的强度和第一次变化的强度是相等的。
一个线性检测器得出第二次增大的程度是第一次的10倍,显然,第一次增长0.9w。第二次增长9w。第二次变化比第一次变化大10倍。
人类听觉对强度的响应成对数关系。因此,对数经常用于描述音频系统的工作情况。对数增益非常方便,得到广泛应用。当初我们在音频系统引入的对数增益现在已经成为放大器性能的一个通用标准。它用于无线电广播系统,视频系统和各种有电子增益的地方。
常用对数以10为底,例如:
![]()
任何正数都可以转化为一个常用对数。
例4
用科学计算器计算2138的常用对数。输入2138,然后按“log”键:
显示≈3.33
功率增益经常用分贝(db)为单位进行测量,db是一个对数单位,db可以用这个公式求出:
分贝功率增益db=
…………………….(1)
增益的分贝数是基于常用对数,常用对数以10为底,上面的公式里表示为log10(以10为底),为简便,以后 lg就是指log10。
小于1的数的对数值是负的,由上面的公式这意味着电子系统的某一部分的输出小于输入,有一个负增益(- db)。
让我们用式(1)解释前面给例子。第一次强度增加:
分贝功率增益db=
![]()
因此,第一次强度增加为10 db 。第二次强度的增加:
分贝功率增益db=
![]()
第二次强度增加也等于10 db。因为db是一个对数单位,而人的听觉也是分辨对数,所以这两个10db的变化听起来好像是一样的。普通人可以分辨出小到1db的变化,对大多数人很难分辨出小于1db的变化。
图11-2说明分贝增益的重要性这。一个电子系统的五个级或五个部分如图,其中三个级的表现为增益(+db),两个表现为衰减(-db),为了计算图11-2所示系统的整体性能,只需把这些数值相加:
总增益=+10-6+30-8+20=+46db
当系统每个部分的增益或衰减用分贝方式表示,计算整体性能变的非常容易,这就是为什么分贝在电子学里得到广泛应用的原因。
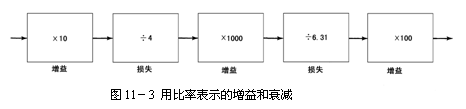
图11-3显示了同样一个系统,每个单元的性能用比例来描述。现在要估算整体性能就不那么方便了。整体性能可以通过以下公式得到:
总增益=
![]()
注意到必须把增益部分相乘,把衰减部分相除。
图11-2和图11-3描述的是同一个系统。一个总增益是+46db,另一个为39,619.65,以db为单位的增益和以比例形式表示的增益是一样的。
db=10×lg39,619.65=10×4.60=46
分贝是基于输出功率与输入功率的比值。它也可以用来描述两个电压比。求db电压增益的方程和用来计算db功率增益的方程有一些不同:
分贝电压增益db=20×
注意到在上述方程中对数乘以20,这是因为功率和电压平方成正比:
![]()
功率增益可以写成:
![]()
如果rout和rin刚好相等,他们可以消掉。那么功率增益可以化简为:
因为u2的对数等于2×lgu,因此:
分贝功率增益db=
![]()
………………………(2)
对于电压放大器,rin和rout相等这一点通常不用考虑。但必须记住如果阻值不等,那么db电压增益将不等于db功率增益。例如,假设一个放大器的电压增益为50,输入电阻为1kω,输出电阻为150ω,它的db电压增益为:
av=
![]()
=34db
如果指定一个输入电压(具体数值多少没关系),就可以求出同一个放大器的功率增益。如果我们给定输入电压为1v,那么由前面提到的电压比,输出电压为50v。现在,输入功率和输出功率可以计算:
pin=
![]()
=1mw
pout=
![]()
16.7w
该放大器的分贝功率增益为:
ap=
![]()
=42.2db
注意这里与分贝电压增益并不相等。
另一个例子,假设一个放大器的电压增益为1,输入电阻为50,000ω,输出电阻为100ω,那么这个放大器的db电压增益为:
au=20×lg1=0db
假设输入信号为1v:
pin=
![]()
20μw
pout=
![]()
10mw,
放大器的功率增益为:
ap=
![]()
27db。
因为rin并不等于rout,所以我们看到分贝功率增益并不等于分贝电压增益。我们看到另一个有趣的事实是,一个放大器可能没有电压增益,但能提供显著的功率增益。
例5
一个100w的放大器具有10db的功率增益,需要多大的输入信号才能驱动放大器得到满功率输出。功率增益对应于:
,因此需要的输入信号功率是输出功率的1/10:
![]()
例6
发射机通过一条长的同轴电缆输送到天线。发射机输出功率为1kw,但只有500w到达天线。同轴电缆的工作性能用db表示为多少?500w只有输入功率的一半,因此,功率除以2,表示为-3db,这条电缆的工作性能可以用不同的方法来描述:
1 电缆增益为-3db
2电缆衰减为3db
3 电缆衰减为-3db
第一种说法在工程上是正确的,负db增益实际表示衰减。第二种说法也是正确的,“衰减”这个词表示3db在系统计算中使用时,3db值前面要加了一个负号,第三种说法是不正确的,因为“衰减”表示在db值前加负号,结果就变成了-(-3db)=+3db,
例7
在5khz时一个低通滤波器的响应规定为-6db,技术人员检测滤波器输出发现1khz时为1v,5khz时,降到0.5v,滤波器正常工作吗?电压除以2等于-6db。滤波器正常工作。
例8
一个放大器当输入信号为100mw时,输出信号为2w。这个放大器的功率增益是多少db?首先算出比率:
20w/0.1w=20
功率增益20可以分解为功率增益为10(+10db)乘以功率增益2(+3db)。把db增益相加:
增益=10db+3db=13db。
例9
一个放大器的电压增益为60db,如果输入信号为10μv,输出信号为多少?
电压增益为20db对应的放大倍数为10;60db=3×20db,因此60db的增益时信号应乘以10的3次方:
uout=uin×103=10μv×1000=10mv
解决某些问题时需要一些代数方法来处理,下面的例子就演示这种情况。
例10
用测量一个高频波形,示波器生产厂家说明目前测量频率下的响应是-3db。如果屏幕显示峰峰值为7v,实际信号值为多少?先把已知信息代入db方程转换为电压:
两边同除以20:
方程变形并求解:
有时候db制会被误用。以db形式给出的通常是绝对值。例如,我们说一组音乐的声音强度为90db,如果没有有一个商定的参考强度,就不知实际的声压。声音中使用的考强度是压强为每平方厘米0.0002达因(dyn/cm2)或每平方米2×10-5牛顿(n/m2)为0db。这就是人的听力的阈值。现在,如果又有一个压强和参考压强相比较这个声强的db数就可以求出。例如,一个喷气式发动机能产生2000dyn/cm2的声强:
声音电平=
![]()
=140db
(对数值乘以20是因为声音功率和声音压强的平方成正比)。在家里一般声强为0.063dyn/cm2,跟参考压强相比较得到:
声音电平=
![]()
=50db
注意到非常有趣的是分贝标度把人的听力的阈值定为0db,而把耳朵能感到振动的阈值定为120db。你可能会注意到,一个非常大的声音除了能听到外耳朵还能感觉到。声音强度如果很大就会造成伤害。听力总的动态范围为140db,任何超过140db的声音(喷气式发动机)对一个人来说听起来都是一样大的(即使它会造成更大伤害)。
声音强度通常用dba标度来计量。这个标度把人听力的阈值也设为0db。a是指在测量中进行加权。滤波器使频率响应满足人听力的要求。实验证实,加权使仪器报告和紧密匹配人耳的感知,dba标度经常用来确定工人是否需要听力保护。例如,90dba是一周总工时(40小时)的最大安全承受值。一些常用的强度如下:
耳语 30dba
交谈 60dba
繁忙的城市街道 80dba
较近的汽车喇叭 100dba
较近的雷声 120dba
dbm标度在电子通讯中得到广泛使用。这个标度指定0db代表参考强度是1mw。音频和微波的信号和信号源经常用dbm来校准。根据这个参考强度,一个0.25w的信号是:
功率电平=
![]()
+24dbm
一个40μw的信号是:
功率电平=
-24dbm