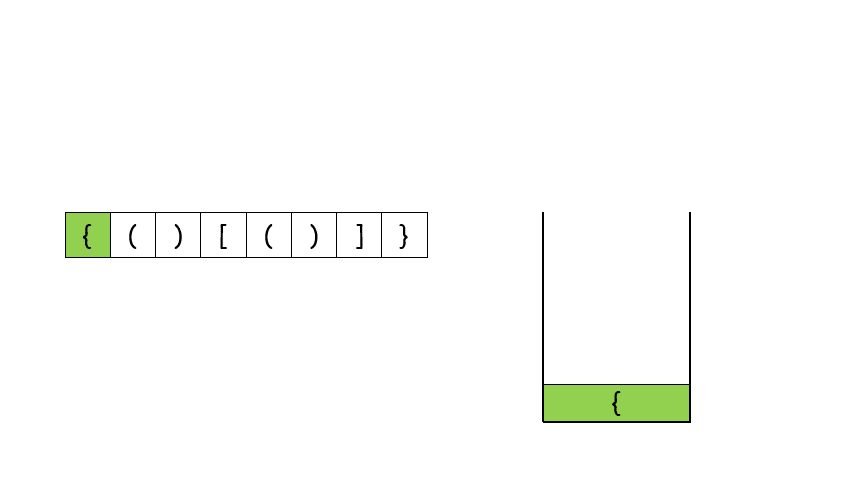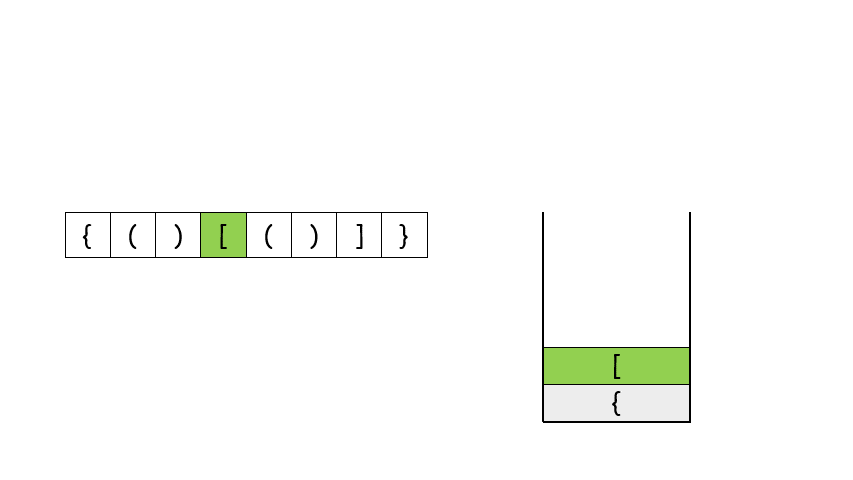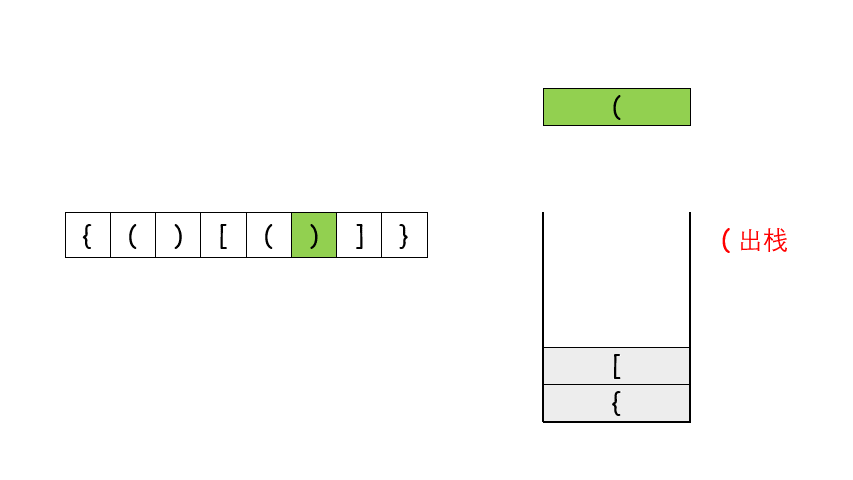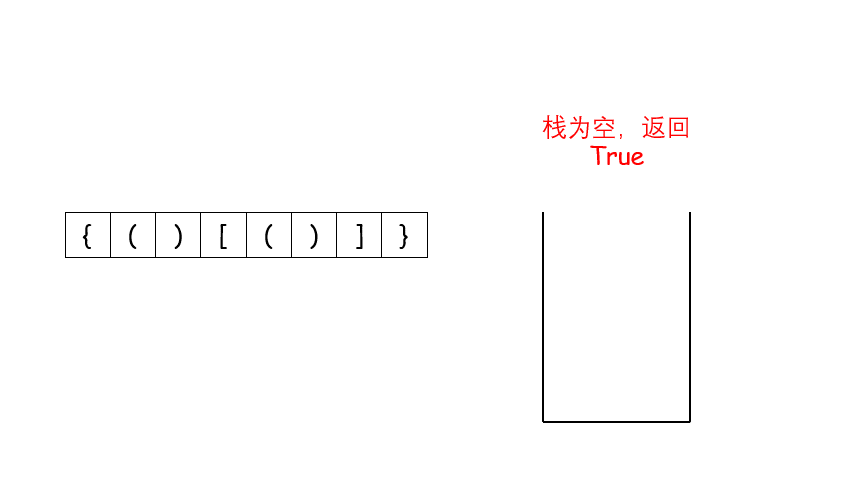【深入解析:数据结构栈的魅力与应用】
本章重点
栈的概念及结构
栈的实现方式
数组实现栈接口
栈面试题目
概念选择题
一、栈的概念及结构
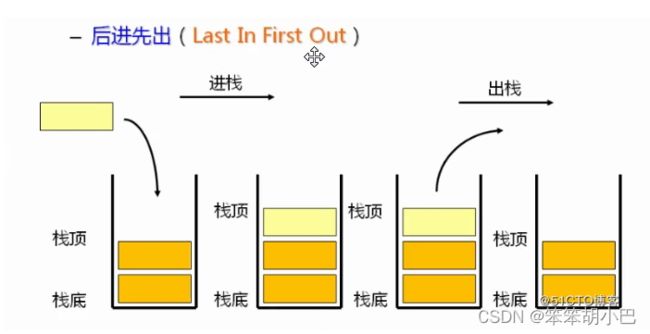
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端 称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈:栈的删除操作叫做出栈。出数据也在栈顶。
- 栈顶Top:线性表允许插入和删除的那一端。
- 栈底Bottom:固定的,不允许进行插入和删除的另一端。
- 空栈:不含任何元素的空表。
二、栈的实现方式
由于栈只能在栈顶操作,所以栈的实现一般可以使用数组或者链表实现,相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。单链表的尾插需要遍历结点,这里使用带头双向循环链表也可,但是空间销毁大。单链表也可以实现,我们就需要让栈顶是头结点,栈底是尾结点,这样入栈就是头插,效率高。
1.顺序堆栈

根据前边的分析可知,顺序堆栈和顺序表的数据成员(元素)是相同的,不同之处是,顺序堆栈的入栈和出栈操作只能对当前栈顶元素进行。
顺序堆栈的存储结构如图3-2所示。其中,a0,a1,a2,表示顺序堆栈要存储的元素序列,stack 表示顺序堆栈存放元素的数组,capacity 表示顺序堆栈数组stack的内存单元容量(表示目前允许存储的元素最大个数),top表示顺序堆栈数组stack的当前栈顶位置。
2.链式堆栈
堆栈有两端,插入元素和删除元素的一端为栈顶,另一端为栈底。对链式堆栈来说,显然,若把靠近头指针的一端定义为栈顶,则插入元素和删除元素时不需要遍历整个链,其时间复杂度为0(1);若把远离头指针的一端定义为栈顶,则每次插入元素和删除元素时都需要遍历整个链,其时间复杂度为0(n)。因此,链式堆栈都设计成把靠近头指针的一端定义为栈顶。链式堆栈的头结点对操作实现的影响不大,因此可有可无。依次向带头结点链式堆栈输入a0,a1,a2,…….an-1后,带头结点链式堆栈的结构示意图如图3-3所示。
三、数组实现栈接口
// 下面是定长的静态栈的结构,实际中一般不实用,所以我们主要实现下面的支持动态增长的栈
typedef int STDataType;
#define N 10
typedef struct Stack
{
STDataType a[N];
int top; // 栈顶
}Stack;
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top; // 栈顶
int capacity; // 容量
}Stack;
// 初始化栈
void StackInit(Stack* ps);
// 入栈
void StackPush(Stack* ps, STDataType data);
// 出栈
void StackPop(Stack* ps);
// 获取栈顶元素
STDataType StackTop(Stack* ps);
// 获取栈中有效元素个数
int StackSize(Stack* ps);
// 检测栈是否为空,如果为空返回0,如果不为空返回非零结果
int StackEmpty(Stack* ps);
// 销毁栈
void StackDestroy(Stack* ps);
1.初始化栈:void StackInit(Stack* ps)
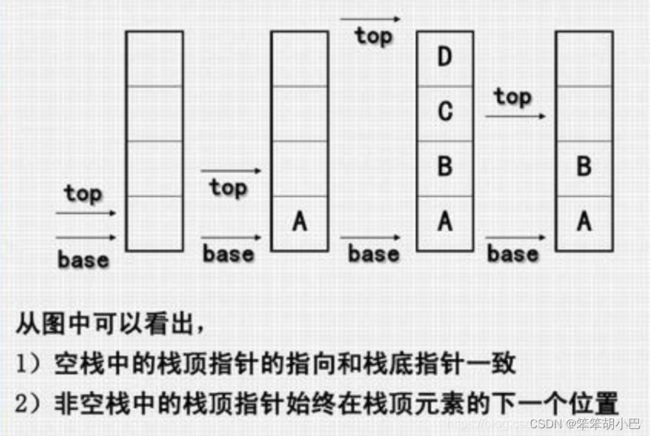
初始化这里我们先不设置容量,后续入栈再申请空间即可,这里需要注意top的值,我们设置的值是0,它是表示非空栈中的栈顶指针始终在栈顶元素的下一个位置上。
// 初始化栈
void StackInit(Stack* ps)
{
assert(ps);
ps->a = NULL;
ps->top = 0;//表示栈顶元素的下一个位置
ps->capacity = 0;
}2.入栈:void StackPush(Stack* ps, STDataType data)
满栈:当我们使一个元素入栈的之前,我们往往需要判断一下栈是否为满栈,防止发生上溢的情况。因为我们定义了一个capacity来表示当前已经分配的存储空间,所以我们可以用ps->top == ps->capacity 来判断当前使用的栈空间是否满了。所以当ps->top == ps->capacity时表示已经满了。
满栈我们要首先追加存储空间,然后才能将元素入栈。realloc()函数可以申请空间,如果realloc第一个参数为空,那么realloc的功能就类似于malloc,这也是为什么我们前面初始化没有开辟空间的原因,写在这里能省大量的代码。
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
if (ps->top == ps->capacity)
{
int newCapacity = (ps->capacity == 0) ? 4 : ps->capacity * 2;
//如果ps->a == NULL,功能相当与malloc
STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newCapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
ps->a = tmp;
ps->capacity = newCapacity;
}
ps->a[ps->top] = data;
ps->top++;
}3.出栈:void StackPop(Stack* ps)
出栈时我们首先要判断栈是否为空栈,由于是顺序栈,我们只需要判断ps->top > 0即可判断当前栈的情况。
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
//保证不为空
assert(ps->top > 0);
ps->top--;
}4.获取栈顶元素:STDataType StackTop(Stack* ps)
取栈顶元素同样需要判断是否为空栈,空栈也不能取出任何数据,所以这里强制断言,一旦为空栈直接程序报错
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
//保证不为空
assert(ps->top > 0);
return ps->a[ps->top - 1];
}5.获取栈中有效元素个数:int StackSize(Stack* ps)
由于top是非空栈中的栈顶指针始终在栈顶元素的下一个位置上,所以top就是当前栈中有效元素个数
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->top;
}6.检测栈是否为空,如果为空返回0,如果不为空返回非零结果:int StackEmpty(Stack* ps)
// 检测栈是否为空,如果为空返回0,如果不为空返回非零结果
int StackEmpty(Stack* ps)
{
if (ps->top != 0)
return ps->top;
else
return 0;
}7.销毁栈:void StackDestroy(Stack* ps)
销毁栈只需将申请的空间释放,再把设置的大小和容量设施为0即可。
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps);
ps->a = NULL;
ps->top = 0;
ps->capacity = 0;
}
四、栈面试题目
括号匹配问题。OJ链接
当开始接触题目时,我们会不禁想到如果计算出左括号的数量,和右括号的数量,如果每种括号左右数量相同,会不会就是有效的括号了呢?
事实上不是的,假如输入是 [ { ] },每种括号的左右数量分别相等,但不是有效的括号。这是因为结果还与括号的位置有关。
仔细分析我们发现,对于有效的括号,它的部分子表达式仍然是有效的括号,比如 { ( )[ ) ] } 是一个有效的括号,( )[ { } ] 是有效的括号,[ ( ) ] 也是有效的括号。并且当我们每次删除一个最小的括号对时,我们会逐渐将括号删除完。比如下面的例子。
这个思考的过程其实就是栈的实现过程。因此我们考虑使用栈,当遇到匹配的最小括号对时,我们将这对括号从栈中删除(即出栈),如果最后栈为空,那么它是有效的括号,反之不是。
bool isValid(char* s)
{
Stack st;
StackInit(&st);
char topVal;
while (*s)
{
switch (*s)
{
case'(':
case'[':
case'{':
StackPush(&st, *s);
break;
case')':
case']':
case'}':
//数量不匹配
if (!StackEmpty(&st))//栈为空
{
StackDestroy(&st);//防止内存泄露
return false;
}
topVal = StackTop(&st);
StackPop(&st);
//顺序不匹配
if (*s == ')' && topVal != '('
|| *s == ']' && topVal != '['
|| *s == '}' && topVal != '}')
{
StackDestroy(&st);//防止内存泄露
return false;
}
break;
}
++s;
}
//栈不为空,此时只有右括号,false,说明数量不匹配
int ret = StackEmpty(&st);
StackDestroy(&st);
if (ret == 0)
return false;
else
return true;
}五、概念选择题
1.一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈,然后再依次出栈,则元素出栈的顺序是( )。
- A 、12345ABCDE
- B 、EDCBA54321
- C 、ABCDE12345
- D 、54321EDCBA
元素出栈的顺序遵循后进先出(Last-In-First-Out,LIFO)原则,因此选择B
2.若进栈序列为 1,2,3,4 ,进栈过程中可以出栈,则下列不可能的一个出栈序列是()
- A 1,4,3,2
- B 2,3,4,1
- C 3,1,4,2
- D 3,4,2,1
A:1入栈后出栈,2,3,4入栈,4出栈,3出栈,2出栈,可能。
B:1,2入栈,2出栈,3入栈,3出栈,4入栈,4出栈,1出栈,可能。
C:1,2,3入栈,3出栈,接下来应该是2出栈或者4入栈,不可能1出栈,不可能。
D:1,2,3入栈,3出栈,4入栈,4出栈,2出栈,1出栈,可能。
本章结束啦!!!