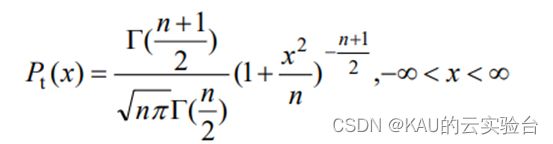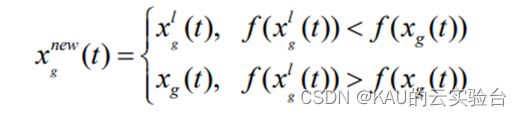自适应混沌蜣螂优化算法及其MALTAB实现

本文改进主要参考：

S. Li and J. Li, “Chaotic dung beetle optimization algorithm based on adaptive t-Distribution,” 2023 IEEE 3rd International Conference on Information Technology, Big Data and Artificial Intelligence (ICIBA), Chongqing, China, 2023, pp. 925-933, doi: 10.1109/ICIBA56860.2023.10165106.

作者在上一篇文章中介绍了蜣螂优化算法(dung beetle optimizer，DBO)，其具有收敛速度快和准确率高的特点，可以有效地解决复杂的寻优问题。然而虽然其具有比PSO、GWO等算法更好的优化性能，但其存在初始种群分布不均匀、全局探索和局部开发能力不平衡、易陷入局部最优等缺点。

因此，受混沌映射和自适应T分布的启发，提出对DBO算法进行改进。混沌映射如Logistic映射和Tent映射，能够提高初始种群在搜索空间的分布质量，加强其全局搜索能力；而自适应t分布能在迭代的不同时期提高算法的全局/局部搜索能力。两种方法相辅相成，能够帮助DBO算法获得更好的优化性能。

实验部分，本文将改进的DBO算法与DBO以及一些常用的智能算法在9个标准测试函数上进行实验对比，以验证改进的有效性。

00 文章目录

1 蜣螂优化算法原理
2 自适应混沌蜣螂优化算法
3 代码目录
4 实验结果
5 源码获取

01 蜣螂优化算法原理

关于蜣螂算法原理作者在上一篇文章中已经作了介绍

蜣螂优化算法原理及其MALTAB实现

02 自适应混沌蜣螂(Adaptive Chaos DBO，AC-DBO)优化算法

2.1 改进的Tent混沌映射

与其他群智能算法一样，原始DBO在求解复杂问题时，通过随机生成位置的方法初始化种群的个体位置，会导致种群的多样性低，对问题进行寻优的收敛速度比较慢。为了能够让个体在算法开始时有较高的全局搜索能力，需要让种群的位置均匀分布在整个问题的解空间内，因此使用混沌算子对种群进行初始化。

混沌作为一种非线性的自然现象，以其混沌序列具有遍历性、随机性等优点，被广泛用于优化搜索问题。利用混沌变量搜索显然比无序随机搜索具有更大的优越性[1]。

目前文献中常用的混沌扰动方程有Logistic映射和Tent映射等。Logistic映射在作者前面的文章中介绍过，由文献[2]可知Logistic映射的分布特点是:中间取值概率比较均匀,但在两端概率特别高,因此当全局最优点不在设计变量空间的两端时,对寻找最优点是不利的。而Tent混沌映射具有比Logistic混沌映射更好的遍历均匀性和更快的搜索速度。下图中展示了Logistic和Tent的混沌序列：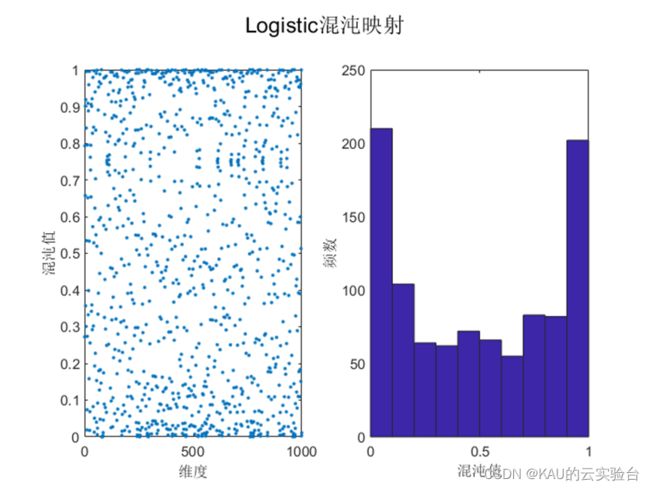

可以看到，Logistic混沌映射在边界区域取值概率明显更高，而Tent在可行域的取值概率更为均匀，因此若将Logistic混沌映射用于初始化种群时，其混沌序列的不均匀性会影响算法寻优的速度和精度。因此本文利用Tent的遍历性产生更为均匀分布的混沌序列，减少初始值对算法优化的影响。

Tent混沌映射的表达式如下：

分析Tent混沌迭代序列能够发现序列中存在小周期,并且存在不稳周期点. 为避免Tent混沌序列在迭代时落入小周期点和不稳定周期点,在原有的Tent 混沌映射表达式上引入一个随机变量rand(0, 1) /N ,则改进后的Tent混沌映射表达式如下[3]:

其中: N 是序列内粒子的个数。引入随机变量rand(0, 1) /N 不仅仍然保持了Tent混沌映射的随机性、遍历性、规律性,而且能够有效避免迭代落入小周期点和不稳定周期点内。本文算法引入的随机变量,既保持了随机性, 又将随机值控制在一定的范围之内,保证了Tent混沌 的规律性.根据Tent混沌映射的特性。改进的Tent混沌序列效果如下：

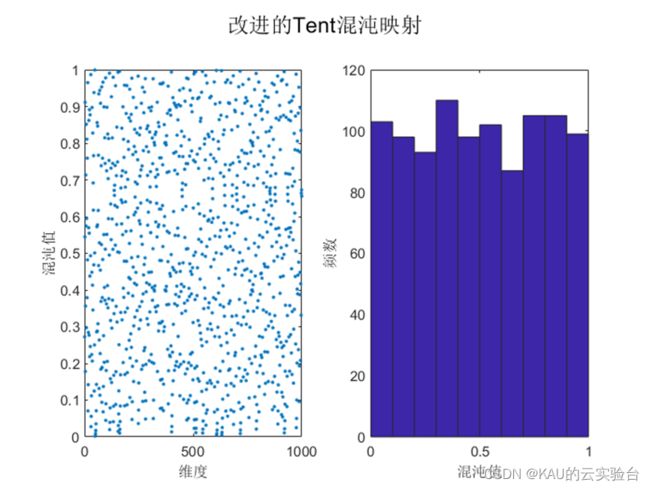
由图可知，改进后的Tent混沌映射其均匀性得到了提高，因此本文以改进Tent混沌性来代替蜣螂优化算法的随机初始化，以提高和改善初始种群在搜索空间上的分布质量，加强其全局搜索能力，从而提高算法求解精度。

2.2 自适应t分布

t分布也叫学生t分布，包含自由度参数n。n的值决定t分布曲线的形状，n值越小，则曲线越平坦，n值越大，则曲线越陡峭。

t分布的概率密度函数为:

式中，t为自由度参数，x 为扰动力度，Γ( )为伽玛函数。当t(n→∞)→N(0,1)时，t(n→1)=C(0,1)，N(0,1)为高斯分布，C(0,1)为柯西分布。高斯分布和柯西分布是t分布的两种边界特例[4]，它们的函数分布如图2所示。

当算子发生柯西突变时，算法的全局搜索性能较好，种群多样性较高。当算子发生高斯突变时，算法收敛速度更快，局部寻优能力更强。

t分布结合了柯西分布和高斯分布的优点，在自由度参数n从1→∞的过程中，可以通过t分布突变算子来平衡和提高算法的全局/局部搜索能力。因此，本文采用自由度参数n=iter的t分布来优化个体的搜索方向和距离，步长会随着迭代次数的增加而自适应变化。采用自适应t分布突变策略对蜣螂位置进行扰动的方程如下：

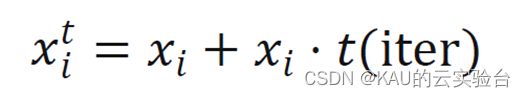
式中，xti为突变后的蜣螂位置，xi为第i只蜣螂个体位置，t(iter)为以迭代次数iter为自由度的t分布。

在迭代开始时，t分布突变类似柯西突变，此时算法具有良好的全局探索能力，增加了种群的多样性，且跳出局部最优的能力也增强了。随着迭代次数的增加，t分布突变近似于高斯突变，提高了算法的局部开发能力，其对于整个种群的扰动力度也从强到弱转化。通过引入自适应t分布突变作为一种改进的搜索策略，能够有效增强算法的优化性能，有利于提高算法逃避局部最优的能力。

通过自适应t分布突变扰动策略虽然能增强算法全局搜索和跳出局部最优的能力，但是没法确定扰动之后得到的新位置一定比原位置的适应度值要好，因此在进行变异扰动更新后，加入贪婪规则，通过比较新旧两个位置的适应度值，确定是否要更新位置。

其中， xnewg(t)为经过贪婪规则更新后的个体位置，xlg(t)为扰动后的个体，xg(t)为扰动前的个体， f ()代表粒子适应度函数。

2.3 自适应混沌蜣螂优化算法步骤

综上所述，自适应混沌蜣螂优化算法主要分为六个步骤。

1）初始化种群大小，迭代次数，t分布概率等参数

2）使用改进的Tent混沌映射初始化蜣螂种群

3）根据目标函数计算所有蜣螂位置的适度值；

4）更新所有蜣螂的位置；

5）判断每个更新后的蜣螂是否出了边界；

6）若随机数rand小于给定P值，则根据t分布突变策略进行扰动，产生新解

7）根据贪婪规则确定是否更新

8）更新当前最优解及其适度值；

9）重复上述步骤，在达到最大迭代次数后，输出全局最优值及其最优解。

流程图如下：

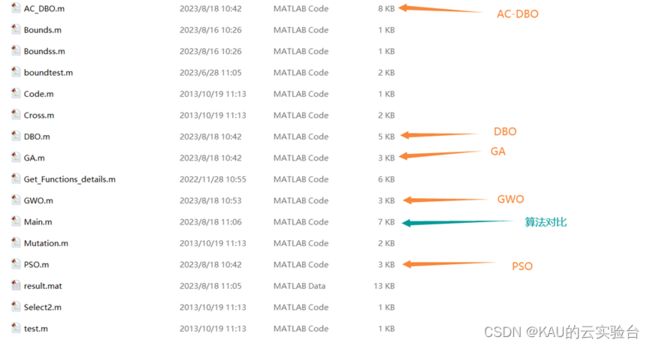
03 代码目录

代码注释完整，其中部分程序如下：

04 实验结果

在本节中，通过单峰，多峰，固定多峰共9个经典测试函数验证AC-DBO的搜索性能，通过仅具有一个全局最优值的单峰函数来测试算法的局部搜索能力，并使用多峰函数来评估全局搜索能力。将改进的蜣螂优化算法与另4种被广泛研究的优化算法(PSO、GA、GWO、DBO)进行比较。

为保证实验公平性，所有算法的迭代次数与种群数都设置为100。

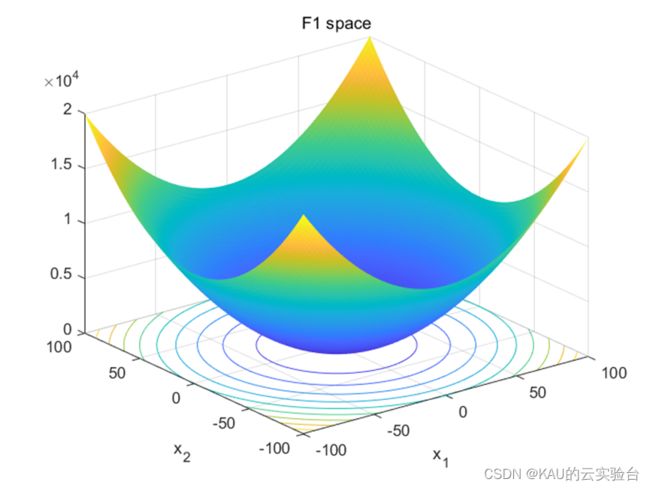
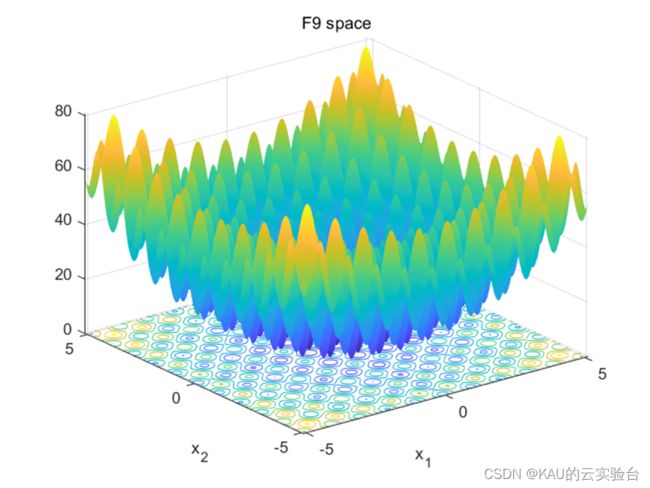
单峰函数采用F1,F2,F3。多峰函数采用F9,F10,F11。固定多峰函数采用F19,F20,F21。部分函数样图如下：

利用上述的5种优化算法对共计9种测试函数进行寻优，结果如下：

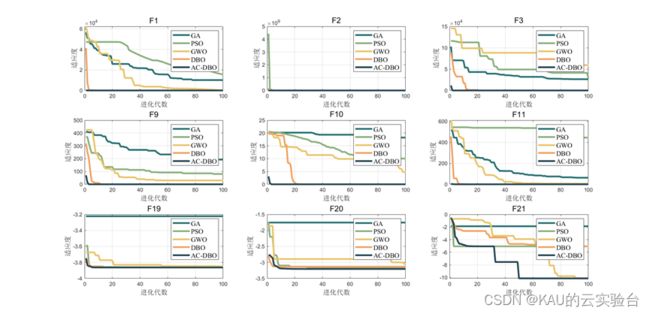
由图可以看出，改进后的算法在搜索精度以及收敛速度上皆优于其他算法，其性能得到了显著提高。

05 源码获取

在作者微信公众号：KAU的云实验台 获取

参考文献

[1] 张云鹏,左飞,翟正军.基于双Logistic变参数和Cheby-chev混沌映射的彩色图像密码算法[J.西北工业大学学报, 2010,28(4): 628-632.

[2] 江善和,王其申,汪巨浪.一种新型SkewTent映射的混沌混合优化算法[J.控制理论与应用, 2007,24(2): 269-273.

[3] 张娜,赵泽丹,包晓安,等.基于改进的Tent混沌万有引力搜索算法[J].控制与决策,2020,35(4):893-900.

[4]Fangjun Zhou ， Xiangjun Wang ， Min Zhang ． Evolutionary Programming Using Mutations Based on the t Probability Distribution[J]．2008.36(4):667-671．

另：如果有伙伴有待解决的优化问题（各种领域都可），可以发我，我会选择性的更新利用优化算法解决这些问题的文章。

如果这篇文章对你有帮助或启发，可以点击右下角的赞(ง•̀_•́)ง(不点也行)