数据结构——顺序队列【c语言版】

队列（quque）简称队，只允许在表的一端输入，在表的另一端删除(操作受限制的线性表)，

把进行插入的一段叫做队尾（表尾），把进入删除的一端叫做队首或队头（表头）。

队列最主要的特点：先进先出，FIFO（first in first out）

队列有其实有三种：顺序队列、 循环队列、链式队列

        下面是采用采用顺序存储结构来实现的顺序队

        假设栈的元素个数最大不超过正整数MaxSize，所以元素具有同一数据类型（ElemType），用下来方式来声明顺序队列的类型SqQueue：

#define MaxSize 128  //队列的最大容量

typedef int ElemType;  //队列中元素类型

typedef struct 
{
    ElemType data[MaxSize];
    int front;   //存储队头元素前一个单元的下标
    int rear;    //队尾指针
}SqQueue;

对于顺序队来说，有以下四个非常重要的要素：

        1.队空条件：SQ->front == SQ->rear ==  -1

        2.队满条件：SQ->rear == MaxSize - 1

        3.进队操作：先将rear+1，再将元素e放在rear指向的位置

        4.出队操作：先将front+1，再将取出front指向的位置上的元素

1）队列初始化

        构造一个空的队列SQ，将front和rear指针都指向-1，代码如下：

void InitQueue(SqQueue *SQ)
{
    SQ->front = SQ->rear = -1;  //把对头和队尾指针同时置-1
 }

2)判断队列是否为空

        顺序队列中，判断队列是否为空，只需要判断SQ->front == SQ->rear的条件成立即可，代码如下：

//判断队列为空

int IsEmpty(SqQueue* SQ)
{
    if (SQ->front == SQ->rear)
    {
        return 1;
    }
    return 0;
}

3）判断队列是否为满

                顺序队列中，判断队列是否为满，只需要判断SQ->rear == MaxSize - 1的条件成立即可，代码如下：

//判断队列是否为满

int IsFull(SqQueue* SQ)
{
    if (SQ->rear == MaxSize-1) 
    {
        return 1;
    }
    return 0;
}

4）入队

        在队列不满条件下先将rear+1，再将元素e放在rear指向的位置，因此该操作需要先判断队列是否已满，避免上溢，这里可以调用IsFull(SqQueue* SQ)来判断，代码如下：

//入队,先将rear+1，将元素e插入到队列SQ中

void EnterQueue(SqQueue* SQ,ElemType e)
{
    if (IsFull(SQ))
    {
        printf("队列已满\n");
        return 0;
    }
    SQ->rear = SQ->rear + 1;     //队尾指针后移一位
    SQ->data[SQ->rear] = e;  //在队尾插入元素e
    
}

5)出队

        在队列不空条件下先将front+1，再将取出front指向的位置上的元素，因此该操作需要先判断队列是否为空，避免下溢，这里可以调用IsEmpty(SqQueue* SQ)来判断，代码如下：

//出队，先将队头指针front后移一位,取出front指向的元素e出
int DeleteQueue(SqQueue* SQ,ElemType e)
{
    if (IsEmpty(SQ))
    {
        printf("队列为空！\n");
        return 0;
    }
    SQ->front = (SQ->front)+1;      //队尾指针后移一位
    e = SQ->data[SQ->front];      //出队元素值
    
    return e;
}

6）打印队列中的元素

        从队首到队尾，代码如下：

//打印队列中的与元素

void PrintQueue(SqQueue* SQ)
{
    assert(SQ);    
    int i = SQ->front;
    while(irear)
    {
        printf("%-3d", SQ->data[i]);
        i++;
    }
    printf("\n");
}

下面是入队、出栈以及打印出队列元素的操作：

int main()
{
    SqQueue SQ;
    ElemType e;
    //初始化队列
    InitQueue(&SQ);
    //入队
    EnterQueue(&SQ, 1);
    EnterQueue(&SQ, 2);
    EnterQueue(&SQ, 3);
    EnterQueue(&SQ, 4);
    EnterQueue(&SQ, 5);
    EnterQueue(&SQ, 6);
    EnterQueue(&SQ, 7);
    EnterQueue(&SQ, 8);
    EnterQueue(&SQ, 10);
    EnterQueue(&SQ, 12);
    EnterQueue(&SQ, 15);
    EnterQueue(&SQ, 16);

   
    
	//出队
    printf("出队元素为：%d\n", DeleteQueue(&SQ, e));
    printf("\n");
    
    printf("出队元素为：%d\n", DeleteQueue(&SQ, e));
    printf("\n");
    
    printf("队列中的元素为：");
    PrintQueue(&SQ);
    printf("\n");
 
  
   
    return 0;
}

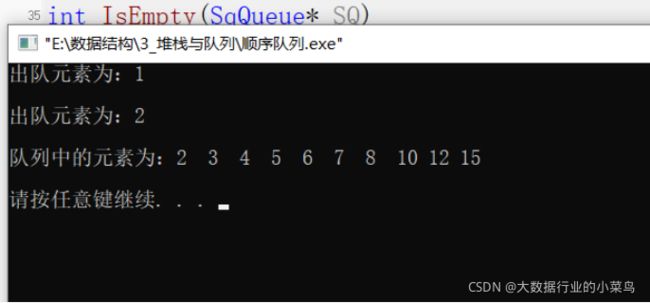
测试结构如下：

总结：

        实际上，我们非常不建议使用顺序队，因为无论是入队还是出队，它们的指针front，rear都是加1，当队列中有元素出队而SQ->rear == MaxSize时，再进行入队，会显示队满，但其实front的前面还要很多空间，造成空间的浪费，存在假溢现象， 所以一般情况下都采用循环队列的方法来解决。

最后再附上完整代码：

/*
设立一个存储队头元素前一个单元的下标front ，一个队尾指针rear ，分别指向存储队头元素前一个单元的下标和队尾元素。

  初始化：front=rear=-1。
  队列为空：front=rear。
  队满：rear=MaxSize。
  入队：先将rear加1，再将新元素插入rear所指的位置。
  出队：先将real加1，再删取出front所指的元素。
 
*/

#include 
#include 
#include 

#define MaxSize 128  //队列的最大容量

typedef int ElemType;  //队列中元素类型

typedef struct 
{
    ElemType data[MaxSize];
    int front;   //存储队头元素前一个单元的下标
    int rear;    //队尾指针
}SqQueue;

//队列初始化，将队列初始化为空队列
void InitQueue(SqQueue *SQ)
{
    SQ->front = SQ->rear = -1;  //把对头和队尾指针同时置-1
 }

//判断队列为空

int IsEmpty(SqQueue* SQ)
{
    if (SQ->front == SQ->rear)
    {
        return 1;
    }
    return 0;
}

//判断队列是否为满

int IsFull(SqQueue* SQ)
{
    if (SQ->rear == MaxSize-1) 
    {
        return 1;
    }
    return 0;
}

//入队,先将rear+1，将元素e插入到队列SQ中

void EnterQueue(SqQueue* SQ,ElemType e)
{
    if (IsFull(SQ))
    {
        printf("队列已满\n");
        return 0;
    }
    SQ->rear = SQ->rear + 1;     //队尾指针后移一位
    SQ->data[SQ->rear] = e;  //在队尾插入元素e
    
}

//出队，先将队头指针front后移一位,取出front指向的元素e出
int DeleteQueue(SqQueue* SQ,ElemType e)
{
    if (IsEmpty(SQ))
    {
        printf("队列为空！\n");
        return 0;
    }
    SQ->front = (SQ->front)+1;      //队尾指针后移一位
    e = SQ->data[SQ->front];      //出队元素值
    
    return e;
}



//打印队列中的与元素

void PrintQueue(SqQueue* SQ)
{
    assert(SQ);    
    int i = SQ->front;
    while(irear)
    {
        printf("%-3d", SQ->data[i]);
        i++;
    }
    printf("\n");
}
int main()
{
    SqQueue SQ;
    ElemType e;
    //初始化队列
    InitQueue(&SQ);
    //入队
    EnterQueue(&SQ, 1);
    EnterQueue(&SQ, 2);
    EnterQueue(&SQ, 3);
    EnterQueue(&SQ, 4);
    EnterQueue(&SQ, 5);
    EnterQueue(&SQ, 6);
    EnterQueue(&SQ, 7);
    EnterQueue(&SQ, 8);
    EnterQueue(&SQ, 10);
    EnterQueue(&SQ, 12);
    EnterQueue(&SQ, 15);
    EnterQueue(&SQ, 16);

   
    
	//出队
    printf("出队元素为：%d\n", DeleteQueue(&SQ, e));
    printf("\n");
    
    printf("出队元素为：%d\n", DeleteQueue(&SQ, e));
    printf("\n");
    
    printf("队列中的元素为：");
    PrintQueue(&SQ);
    printf("\n");
 
  
   
    return 0;
}