CSAPP malloc实验
实验简介
实现自己的动态内存分配器(malloc、free、realloc)。
预备知识
- 阅读《CSAPP原书第3版》 9.9小节 —— 动态内存分配。
- 阅读writeup的全部内容。
分配器的设计要求
- 处理任意请求序列,分配器不可以假设分配和释放请求的顺序。
- 立即响应请求, 不允许分配器为了提高性能重新排列或缓冲请求。
- 只使用堆。
- 对齐块,以保存任何类型的数据对象。
- 不修改已分配的块,分配器只能操作和改变空闲块。
分配器的设计目标
- 最大化吞吐率 —— 每个
malloc,free执行的指令越少,吞吐率会越好。 - 最大化内存利用率。
实现问题
关键是把握吞吐率和内存利用率之间的平衡。
- 空闲块组织 —— 如何记录空闲块?
- 放置 —— 如何选一个合适的空闲块来放置一个新分配的块? (首次适配/下次适配/最优适配)
- 分割 —— 将一个新分配块放到某个空闲块后,如何处理这个空闲块的剩余部分?
- 合并 —— 如何处理一个刚被释放的块? (立即合并/延迟合并)
实验步骤
代码下载:http://csapp.cs.cmu.edu/3e/malloclab-handout.tar
目标是实现mm.c中的如下函数, 原型如下:
int mm_init(void);
void *mm_malloc(size_t size);
void mm_free(void *ptr);
void *mm_realloc(void *ptr, size_t size);
这里使用两种方式实现malloc,分别如下:
- 隐式空闲链表 + 首次适配/下一次适配。
- 显示空闲链表 + 分离的空闲链表 + 分离适配。
隐式空闲链表法
原书9.9.6节详细介绍了隐式空闲链表法,并贴出了所有源代码。代码实现细节请参考原书或者 https://github.com/PCJ600/MallocLab/tree/br64
隐式空闲链表的形式如下:
- 每个堆块使用边界标记法。头部大小为4字节,前29位表示块大小,后3位表示这个块是否空闲;脚部(ftr)是头部(hdr)的副本。目的是将合并前面的堆块时的搜索时间降到常数。
- 第1个填充字用于8字节对齐访问。考虑64位场景,如不添加填充字,heap_listp的值不能整除8,不满足对齐条件!
- 序言块和结尾块的设计是消除合并时边界条件的技巧。
- 按8字节对齐要求, 一个堆块最小为 4(头部) + 8(payload) + 4(脚部) = 16字节
- 为什么是"隐式"的?—— 因为空闲块是通过头部中大小字段隐含地连接着,从而间接遍历整个空闲块的集合。
1. 初始化堆 —— mm_init函数
mm_init步骤如下:
-
首先在堆上分配16个字节,包括4字节对齐块,8字节序言块,4字节结尾块。
-
调
extend_heap扩展堆,创建初始的空闲块,大小为4096字节。
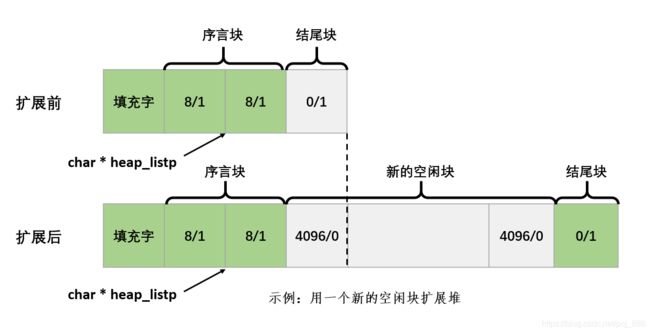
2. 扩展堆 —— extend_heap函数
函数原型: static void *extend_heap(size_t words);
以下两种场景需要扩展堆:
- 调用
mm_init初始化堆时。 - 调用
mm_malloc找不到合适的空闲块时。
举例:堆上扩展4096个字节,堆数组前后变化如下:
3. 释放和合并块 —— mm_free和coalesce函数
调用mm_free释放块,步骤如下:
-
将当前块的头部和脚部中的分配位清零。
-
将这个块与它邻接的前后空闲块进行合并,采用立即合并策略。
调用coalesce合并前后的合并块,原型:static void *coalesce(void *bp);,分四种情况:
- 情况1:前面的块和后面的块都已分配 —— 不可能合并,简单返回bp即可。
- 情况2:前面的块已分配,后面的块空闲 —— 用当前块和后面块的大小之和更新当前块的头部和后面块的脚部。返回bp
- 情况3:前面的块是空闲的,后面的块是分配的 —— 用两块大小之和更新前面块的头部和后面块的脚部。返回
PREV_BLKP(bp) - 情况4:前面和后面的块都是空闲的 —— 用三个块大小之和更新前面块的头部和后面块的脚部。返回
PREV_BLKP(bp)
说的比较啰嗦,以下画图帮助理解:
情况2: 前面的块已分配,后面的块空闲
注意: 如采用下次适配策略,在情况3、情况4合并后可能出现pre_listp指针不再指向一个块的payload段,报payload overlap错!
因此必须更新pre_listp。这里简单将pre_listp指向合并后的新块的payload即可。
情况3: 前面的块是空闲的,后面的块是分配的
4. 分配块 —— mm_malloc
mm_malloc步骤
-
调整请求块的大小,需不低于16字节(8字节对齐要求),并舍入到8的整数倍。
-
根据请求块的大小,搜索空闲链表寻找合适的空闲块:
- 如果找到合适的块,将请求块放置到这个合适的块中,并可选地分割这个块
- 如找不到合适的块,调
extend_heap扩展堆,分配新的空闲块。将请求块放到这个新的空闲块里,并可选地分割这个块
适配算法
分配器搜索空闲块的方式由放置策略决定,常见策略有首次适配、下一次适配等。
-
首次适配: 从头搜索空闲链表,选择第一个合适地空闲块。
-
下一次适配: 从上次查询结束的地方开始搜索空闲链表。
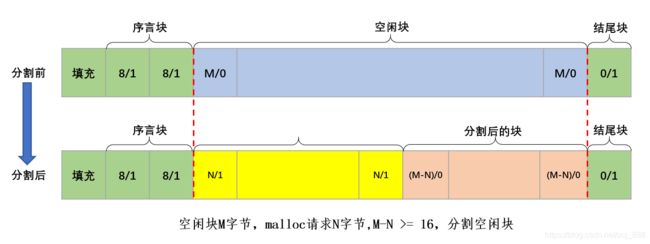
分割策略
如分割后剩下的块不小于最小块大小(16字节),才分割这个块。
设空闲块大小为M字节,malloc请求的块大小为N字节。只有M - N >= 16,才分割这个块。
5. 实现mm_realloc
mm_realloc原型:void *mm_realloc(void *ptr, size_t size)
writeup中提到了mm_realloc的所有实现要点,如下:
- 如果ptr为NULL, 等价于调用mm_malloc
- 如果size为0, 等价于调用mm_free
- 如ptr不为NULL且size不为0, 参考realloc函数的实现:
man 3 realloc
实验结果
执行./mdriver -t traces/ -V,查看详细结果:
首次适配: 44 (util) + 24 (thru) = 68/100
下一次适配:43 (util) + 40 (thru) = 83/100
分离空闲链表法
实现代码参考:https://github.com/PCJ600/MallocLab
使用分离的空闲链表,分配器会维护一个空闲链表的数组。每个空闲链表和一个大小类关联,被组织成某种类型的显式或隐式链表。笔者这里使用以下方案:
- 链表结构为显式的双向链表
- 大小类分为 {16-31},{32,63},{64,127}, …, {4096, 8191}, … 链表个数
MAX_LIST_NUM默认设置为20,可调整。 - 考虑兼容性,分配器需要在32位/64位环境下都能正常运行。
注意事项
- 32位机器上,指针大小为4字节;64位机器上, 指针大小为8字节。可使用
sizeof(intptr_t)表示指针大小,intptr_t类型是ISO C99定义的,可参考/usr/include/stdint.h - 实验要求不使用全局变量,可以将分离链表的头指针放到堆中。
- 默认Makefile采用
-m32选项,64位环境下需要改成-m64。 - 实验涉及大量指针操作,编码极易出错。需掌握基本的gdb调试手段、并编写代码检查堆区和分离链表。
显式的双向链表的堆块结构
-
对于空闲块,
pred保存上一个空闲块的地址,succ保存下一个空闲块的地址。 -
使用双向链表结构,适配算法的时间复杂度从O(块总数)降到O(空闲块总数)。
-
不难得出:32位系统,块至少为16字节;64位系统,块至少为24字节。
如何调试?
- 设置编译选项
-g -O0取消编译优化。 - 设置编译选项
-g3 -gdwarf-2调试宏。 - 可以设置
-DDEBUG宏,通过编译宏控制是否打印调试信息。 - 实现
mm_print函数,在gdb中通过call mm_print()打印堆区和分离链表。
打印堆数组状态和所有分离链表 —— mm_print函数设计
-
打印堆数组中每个块的头部、脚部、大小、分配位、payload指针。
-
打印堆数组中所有分离链表头指针的值。
-
打印每条分离链表的所有块的头部、脚部、大小、分配位、payload指针。
堆区和分离链表检查 —— mm_check函数设计
检查堆区状态,包括:
- 检查序言块、结尾块的指针、大小、分配位是否正确。
- 检查每个块的payload指针是否满足对齐要求。
- 检查每个块的payload指针是否在堆区的合法地址范围内(
mem_heap_lo() ~ mem_heap_hi()之间)。 - 检查每个块的头部和脚部是否一致。
- 检查每个块的大小是否不低于最小块的大小,是否为4/8字节的倍数。
- 采用立即合并策略时,检查不存在任意两个相邻的空闲块。
检查分离链表状态,包括:
-
检查链表中所有指针是否在堆区的合法地址范围内。
-
检查双向链表实现是否正确,是否每个指针A的后继为B时,B的前驱也同时为A。
-
检查分离链表中所有的空闲块是否与堆数组的空闲块中找到并匹配。
-
检查堆数组中每个空闲块是否都能在分离链表中找到并匹配。
-
检查堆数组中每个已占用块是否都不在分离链表中。
针对malloc做如下检查:
- malloc返回前,检查指针p是否在堆数组中,如不在堆数组中说明出错。
- malloc返回前,检查指针p对应的块大小是否不小于malloc请求的大小。
针对free做如下检查:
-
调用free时,先检查指针p是否在堆区的合法地址范围内。
-
调用free时,先检查p是否指向了堆数组中某个已分配块。
实现代码参考: https://github.com/PCJ600/MallocLab/blob/master/mm.c mm_check函数
指针运算、宏定义
#define ALIGNMENT (sizeof(size_t))
#define ALIGN(size) (((size) + (ALIGNMENT-1)) & ~(ALIGNMENT-1))
#define WSIZE 4 // 4字节
#define DSIZE 8 // 双字: 8字节
#define CHUNKSIZE (1 << 12) // 4096字节, 执行extend_heap一次, 堆上扩展的大小
#define PACK(size, alloc) ((size) | (alloc)) // 设置分配位, 前29位表示块大小,后3位表示是否已分配
#define GET(p) (*(unsigned int *)(p))
#define PUT(p, val) (*(unsigned int *)(p) = (val))
#define GET_SIZE(p) (GET(p) & ~(0x1)) // 获取块大小, 这里块大小不会超过2^32字节
#define GET_ALLOC(p) (GET(p) & 0x1) // 判断这个块是否已分配
// 指针类型读写,使用intptr_t兼容32位/64位机器
#define GET_P(p) (*(intptr_t *)(p))
#define PUT_P(p, val) (*(intptr_t *)(p) = (intptr_t)(val))
// 分离链表: |(16-31)|(32-63)|(64-127)|(128-255)| ..... |(2^23,2^24-1)|,这里设置20条链表
#define MAX_LIST_NUM 20 // 分离链表最大数
#define MIN_INDEX 4 // 最小块为16字节, 即2^4。这里MIN_INDEX表示分离链表中第一条链表的最小块大小
#define MIN_BLOCK_SIZE (DSIZE + 2 * sizeof(intptr_t)) // 块大小的最小值,32位为16字节, 64位为24字节
#define PTR(bp) ((char *)(bp)) // 强转成char *类型指针
#define HDRP(bp) ((char *)(bp) - WSIZE)
#define FTRP(bp) ((char *)(bp) + GET_SIZE(HDRP(bp)) - DSIZE)
#define NEXT_BLKP(bp) ((char *)(bp) + GET_SIZE(((char *)(bp) - WSIZE)))
#define PREV_BLKP(bp) ((char *)(bp) - GET_SIZE(((char *)(bp) - DSIZE)))
#define PREV(bp) ((char *)(bp))
#define SUCC(bp) ((char *)(bp) + sizeof(intptr_t))
#define GET_PREV(bp) ((char *)(GET_P(PREV(bp))))
#define GET_SUCC(bp) ((char *)(GET_P(SUCC(bp))))
辅助函数设计
static void insert_node(void *p, size_t size); /* 将大小为size的空闲块插入分离空闲链表 */
static void delete_node(void *p); /* 从分离链表中删除指定块 */
static void *coalesce(void *p); /* 合并空闲块 */
static void *place(void *p, size_t size); /* 放置大小为size的块到p指向的空闲块 */
static void *extend_heap(size_t size); /* 扩展堆 */
/* 在所有分离链表中找合适空闲块,返回空闲块指针 */
static void *find_free_block(size_t size);
/* 将p指向的块插入第idx个分离链表 */
static void insert_node_by_list_index(void *p, size_t size, int idx);
/* 移除第i条分离链表上的节点p; 如p不在链表中,则删除失败返回false,否则返回true */
static int delete_node_by_list_index(void *p, int size, int idx);
insert_node
static void insert_node(void *p, size_t size) {
int list_size;
for (int i = 0; i < MAX_LIST_NUM; ++i) {
list_size = (1 << (MIN_INDEX + i));
if (size > list_size) {
continue;
}
insert_node_by_list_index(p, size, i);
return;
}
}
delete_node
static void delete_node(void *p) {
int i;
int list_size;
int size = GET_SIZE(HDRP(p));
for (i = 0; i < MAX_LIST_NUM; ++i) {
list_size = (1 << (MIN_INDEX + i));
if (size <= list_size) {
break;
}
}
// 查找每条分离链表,尝试从链表中删除p
for ( ; i < MAX_LIST_NUM; ++i) {
if (delete_node_by_list_index(p, size, i)) {
return;
}
}
}
coalesace
static void *coalesce(void *p) {
int prev_alloc = GET_ALLOC(HDRP(PREV_BLKP(p)));
int next_alloc = GET_ALLOC(HDRP(NEXT_BLKP(p)));
int size = GET_SIZE(HDRP(p));
if (prev_alloc && next_alloc) { // 前后块均已分配,不可合并
return p;
}
if (prev_alloc && !next_alloc) { // 前面的块已分配,后面的块未分配
delete_node(p);
delete_node(NEXT_BLKP(p));
size += GET_SIZE(HDRP(NEXT_BLKP(p)));
PUT(HDRP(p), PACK(size, 0));
PUT(FTRP(p), PACK(size, 0));
} else if (!prev_alloc && next_alloc) { // 前面的块未分配,后面的块已分配
delete_node(PREV_BLKP(p));
delete_node(p);
size += GET_SIZE(HDRP(PREV_BLKP(p)));
PUT(FTRP(p), PACK(size, 0));
PUT(HDRP(PREV_BLKP(p)), PACK(size, 0));
p = PREV_BLKP(p);
} else { // 前后两个块都空闲,一次性合并三个块
delete_node(PREV_BLKP(p));
delete_node(p);
delete_node(NEXT_BLKP(p));
size += GET_SIZE(HDRP(PREV_BLKP(p))) + GET_SIZE(HDRP(NEXT_BLKP(p)));
PUT(FTRP(NEXT_BLKP(p)), PACK(size, 0));
PUT(HDRP(PREV_BLKP(p)), PACK(size, 0));
p = PREV_BLKP(p);
}
insert_node(p, size);
return p;
}
place
// 32位系统,块最小为 4 + 2 * 4 + 4 = 16字节
// 64位系统, 块最小为 4 + 2 * 8 + 4 = 24字节
static void *place(void *p, size_t size) {
int max_size = GET_SIZE(HDRP(p));
int delta_size = max_size - size;
delete_node(p);
// 如剩余大小少于最小块大小, 不做分割
if (delta_size < MIN_BLOCK_SIZE) {
PUT(HDRP(p), PACK(max_size, 1));
PUT(FTRP(p), PACK(max_size, 1));
return p;
}
// 否则需要分割,并将分割后的空闲块加到空闲链表
PUT(HDRP(p), PACK(size, 1));
PUT(FTRP(p), PACK(size, 1));
PUT(HDRP(NEXT_BLKP(p)), PACK(delta_size, 0));
PUT(FTRP(NEXT_BLKP(p)), PACK(delta_size, 0));
insert_node(NEXT_BLKP(p), delta_size);
return p;
}
extend_heap
static void *extend_heap(size_t size) {
size = ALIGN(size);
void *p;
if ((p = mem_sbrk(size)) == (void *)-1) {
printf("extend_heap failed! mem_sbrk return -1!\n");
return NULL;
}
PUT(HDRP(p), PACK(size, 0));
PUT(FTRP(p), PACK(size, 0));
PUT(HDRP(NEXT_BLKP(p)), PACK(0, 1));
insert_node(p, size);
return coalesce(p);
}
初始化堆 —— mm_init
int mm_init(void) {
// 4字节对齐块 + MAX_LIST_NUM * DSIZE字节的空闲链表头指针 + 2个4字节序言块 + 4字节结尾块
char *p = mem_sbrk(MAX_LIST_NUM * sizeof(intptr_t) + 4 * WSIZE);
if ((void *)p == (void *)(-1)) {
return -1;
}
// 将所有空闲链表的头指针初始为NULL
for (int i = 0; i < MAX_LIST_NUM; ++i) {
PUT_P(p + i * sizeof(intptr_t), NULL);
}
p += MAX_LIST_NUM * sizeof(intptr_t);
PUT(p, 0); // 4字节对齐块,填0;
PUT(p + WSIZE, PACK(DSIZE, 1)); // 序言块头部,4字节
PUT(p + 2 * WSIZE, PACK(DSIZE, 1)); // 序言块脚部,4字节
PUT(p + 3 * WSIZE, PACK(0, 1)); // 结尾快,4字节
if ((p = extend_heap(CHUNKSIZE)) == NULL) {
return -1;
}
return 0;
}
分配块 —— mm_malloc
void *mm_malloc(size_t size)
{
size = get_malloc_size(size); // 得到调整后的malloc请求大小
// 寻找空闲链表是否有合适的空闲块。如果没找到合适的空闲块, 需要扩展堆
void *p = find_free_block(size);
if (p == NULL) {
if ((p = extend_heap(MAX(size, CHUNKSIZE))) == NULL) {
printf("mm_malloc, extend_heap failed!\n");
return NULL;
}
}
p = place(p, size);
return p;
}
释放块 —— mm_free
void mm_free(void *ptr)
{
int size = GET_SIZE(HDRP(ptr));
PUT(HDRP(ptr), PACK(size, 0));
PUT(FTRP(ptr), PACK(size, 0));
// 将释放后的空闲块重新插入到分离链表中
insert_node(ptr, size);
coalesce(ptr);
}
重分配块 —— mm_realloc
函数原型:void *mm_realloc(void *p, size_t size), 优化点如下:
-
如
size小于原来的块大小,简单返回原块即可。 -
如下一块为空闲块,且
空闲块大小 + 原块大小 >= size, 直接合并这两个块。 -
否则,只能用
malloc申请新的空闲块,复制原块,再调用free释放原块
void *mm_realloc(void *ptr, size_t size) {
if (ptr == NULL || size == 0) {
return NULL;
}
// 如果realloc请求的size小于原来的大小,简单返回原块
size = get_malloc_size(size);
int old_size = GET_SIZE(HDRP(ptr));
if (old_size >= size) {
return ptr;
}
// 考虑下一个块是否空闲块,能否直接合并
int next_alloc = GET_ALLOC(HDRP(NEXT_BLKP(ptr)));
int next_size = GET_SIZE(HDRP(NEXT_BLKP(ptr)));
if (!next_alloc && (next_size >= size - old_size)) {
delete_node(NEXT_BLKP(ptr));
PUT(HDRP(ptr), PACK(next_size + old_size, 1));
PUT(FTRP(ptr), PACK(next_size + old_size, 1));
return ptr;
}
// 只能使用malloc申请新的空闲块,复制原块内容,并调用free释放原块
void *oldptr = ptr;
ptr = mm_malloc(size);
memcpy(ptr, oldptr, old_size);
mm_free(oldptr);
return ptr;
}
实验结果
# ./mdriver -t traces/ -V
Results for mm malloc:
trace valid util ops secs Kops
0 yes 99% 5694 0.000886 6430
1 yes 99% 5848 0.000793 7379
2 yes 99% 6648 0.000903 7359
3 yes 99% 5380 0.000749 7182
4 yes 66% 14400 0.001754 8212
5 yes 96% 4800 0.001114 4308
6 yes 95% 4800 0.001112 4317
7 yes 55% 12000 0.004104 2924
8 yes 51% 24000 0.014884 1612
9 yes 87% 14401 0.001490 9667
10 yes 67% 14401 0.001074 13405
Total 83% 112372 0.028862 3893
Perf index = 50 (util) + 40 (thru) = 90/100
参考资料
《深入理解计算机系统 原书第3版》
https://littlecsd.net/2019/02/14/csapp-Malloclab/
https://www.cnblogs.com/liqiuhao/p/8252373.html