JavaScript 递归算法
文章目录
- 前言
- 一、何为'递归'
- 二、调用栈
-
- 1.观察调用栈运作
- 2.调用栈的限制
- 3.迭代算法和递归算法的比较
- 总结
前言
第一次认识递归这个概念在两年前, 一个递归函数(不是深拷贝)看了好久才看懂, 在函数内部再次调用自己, 返回一个新的值, 再此期间还涉及多次对自己的调用, 这对于当时的我还是太过超前了.
不过直到最近, 我对’递归’的认知也几乎只是这些, 我还是希望能有更深刻的理解.
一、何为’递归’
递归并不像我理解的那样只是’自己调自己’这种, 正相反, '对自身的调用’这一行为包含在递归的范畴内.
在第三版《学习JavaScript数据结构与算法》里对递归的定义是:
递归是一种解决问题的办法, 它从解决问题的各个小部分开始, 直到解决最初的大问题. 递归通常涉及函数调用自身.
但是对于递归函数, 就是特指能够直接或者间接调用自身的函数了.
比如:
function recursiveFunction1 (someParam) {
recursiveFunction2(someParam);
}
但是很明显不能在开发中使用上面这个函数——它会一直执行下去, 无休无止.
因此一个完整的递归函数应当具备基线条件, 即一个不再递归调用的条件, 就像while那样.
如果换成这样的话:
function understandRecursion (doIunderstandRecursion) {
const recursionAnswer = confirm('understand');
if (recursionAnswer === true) return; // 基线条件
understandRecursion();
}
是一个合格的JavaScript递归函数了.
二、调用栈
每当一个函数被一个算法调用, 该函数会进入调用栈的顶部, 而递归函数对自身的调用也将导致更多的自己被压入调用栈, 因为每一次调用都可能依赖上一次调用的结果.
1.观察调用栈运作
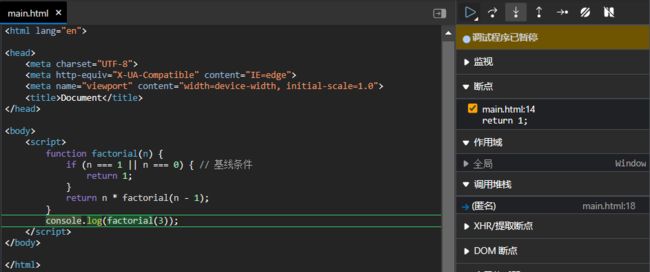
调用栈的情况可以通过浏览器探查, 用一个递归阶乘函数作为例子:
function factorial (n) {
if (n === 1 || n === 0) { // 基线条件
return 1;
}
return n * factorial(n - 1);
}
console.log(factorial(5));
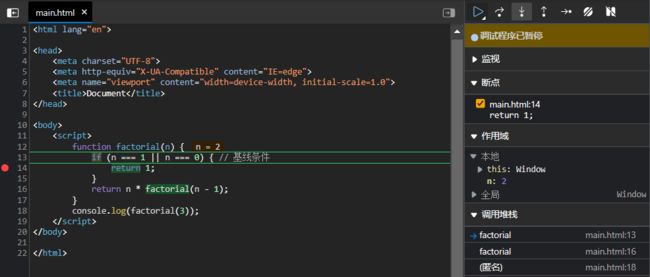
在基线打断点, 暂停执行, 然后刷新页面, 让调用栈回到初始状态:
factorial(3)调用.
factorial(3): 等待factorial(2).
factorial(3)调用.
factorial(2): 等待factorial(1),
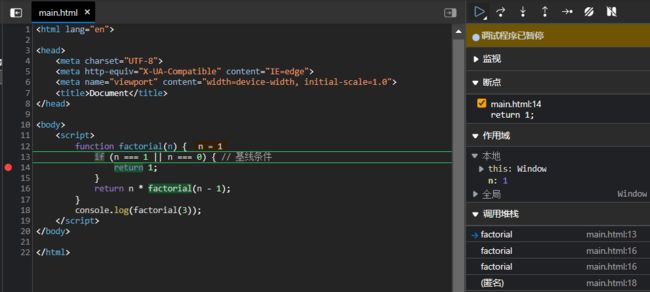
factorial(3): 等待factorial(2).
factorial(3)调用.
2.调用栈的限制
我相信我们都或多或少的遇到过这个错误:
js maximum call stack size exceeded
递归函数在浏览器中并不能无限制的执行下去, 每个浏览器都有自己的调用栈上限, 也许你的递归可以确定并不是无限执行的, 但是浏览器调用栈盛放不了这么多函数, 那么就会抛出错误, 也就是所谓栈溢出(stack overflow error);
根据操作系统和浏览器的不同, 调用栈的承受能力也不同:
let i = 0;
function recursiveFn () {
i++;
recresiveFn();
}
try {
recursiveFn();
} catch (ex) {
console.log(`i = ${i} error: ${ex}`);
}
比如如上递归函数在Chorme v65中执行了15662次塞满了调用栈, 而在Firefox v59中该函数执行了18661次才填满调用栈.
ECMAScript2015出现了尾调用优化的概念, 即如果函数内的最后一个操作是调用函数, 那么会通过跳转指令(jump)而非子程序调用来控制, 即在ECMAScript2015中递归函数的多余消耗甚至能被消除, 递归函数可以一直执行下去.
3.迭代算法和递归算法的比较
以求斐波那契数列为目标, 分别用迭代和递归实现, 检查执行速度.
迭代方案:
function fibonacci_Iterative (n) {
if (n < 1) return 0;
if (n <= 2) return 1;
fet fibNMinus2 = 0;
let fibNMinus2 = 1;
let fibN = n;
for (let i = 2; i <= n; i++) {
fibN = fibNMinus1 + fibNMinus2;
fibNMinus2 = fibNMinus1;
fibNMinus1 = fibN;
}
return fibN;
}
递归方案:
function fibonacci (n) {
if (n < 1) return 0;
if (n < 2) return 1;
return fibonacci(n - 1) + fibonacci(n - 2);
}
明显可见的是递归方案的代码少且易懂.
在递归深拷贝函数内部处理对象循环引用时常用的一种方法是将已经有的值存到weakMap或者Map里, 再次遇到需要使用该值的时候直接使用get从map结构中获取来节省计算量, 这种方法有个专用的名字记忆化.
记忆化是一种保存前一个结果的值的优化技术, 类似于缓存.
如果用记忆化法来求斐波那契数列:
function fibonacciMemoization (n) {
const memo = [0, 1];
const fibonacci = (n) => {
if (memo[n] !== null) return memo[n];
return memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo);
}
return fibonacci;
}
使用记忆化WeakMap来处理深拷贝中循环引用:
function deepCopy(value, weakMap = new WeakMap()) {
if (is.Function(value)) return value;
if (is.Date(value)) return new Date(value.valueOf());
if (is.Symbol(value)) return Symbol(value.description);
if (is.Set(value)) {
const newSet = new Set();
for (const item of value) newSet.add(deepCopy(item), weakMap);
return newSet;
}
if (is.Map(value)) {
const newMap = new Map();
for (const item of value) newMap.set(deepCopy(item[0], weakMap), deepCopy(item[1], weakMap));
return newMap;
}
if (weakMap.has(value)) return weakMap.get(value);
if (!is.Object(value) && !is.Array(value)) return value;
const newObj = is.Array(value) ? [] : addProto(value, {});
weakMap.set(value, newObj);
for (const key in value) {
newObj[key] = deepCopy(value[key], weakMap);
}
return newObj
}
总结
迭代比递归执行起来要快很多, 递归相较于迭代需要的代码更少且更易理解, 另外, 有了尾调用优化, 递归的多余消耗甚至可能被消除.